catalogue
Insert sort
Corresponding letecode link:
Title Description:
To give you the head node of the linked list, please arrange it in ascending order and return the sorted linked list.
Advanced:
Can you sort the linked list under O(n log n) time complexity and constant space complexity?
Example 1:
Input: head = [4,2,1,3]
Output: [1,2,3,4]
Example 2:
Input: head = [-1,5,3,4,0]
Output: [- 1,0,3,4,5]
Example 3:
Input: head = []
Output: []
Tips:
The number of nodes in the linked list is in the range [0, 5 * 104]
-105 <= Node.val <= 105
It mainly introduces quick sort, merge sort, insert sort and bubble sort:
Insert sort:
Problem solving ideas:
The insertion sort of linked list is different from that of array. Array supports random access. The linked list does not support random access. We can move back and forth freely in the array, compare the pointer to the value with the value of the new element, and insert the new element into the appropriate position. We know that the time complexity of the linked list query elements is O (n), and we can only query the elements by traversing the linked list. So how can we put the new elements in the right place?

We can take the first node from the linked list to construct a new linked list:

Insert the remaining nodes into 1 this node. The insertion can be divided into three cases:
1. Head insert
2. Middle insertion
3. Tail plug
Process:
Case 1:
1. If the node of the linked list is inserted into the new linked list, if the node to be inserted is smaller than the head node of the new linked list, we only need to insert the node head into the new linked list
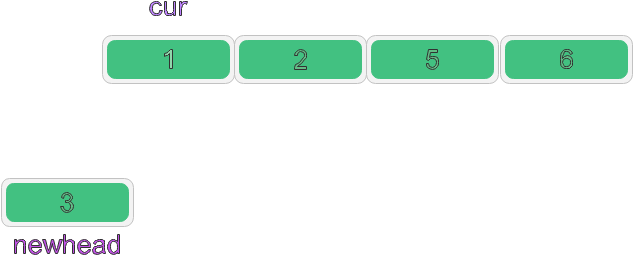
At this time, the val value corresponding to the node pointed to by cur is less than the val value corresponding to newhead. At this time, insert its header, that is: cur - > next = newhead; newhead=cur;
But when we point cur's next to newhead, we can't find the following node. So we need to define a variable next to save the next node
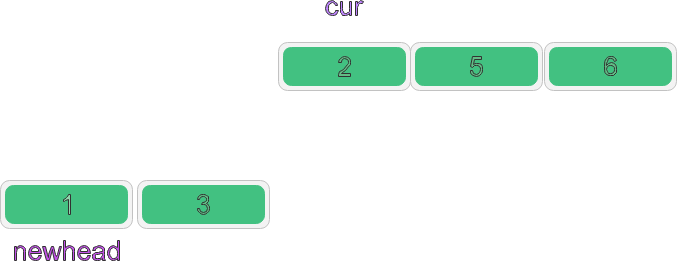
Case 2:
When the val of cur is smaller than that of newhead and is inserted in the middle, we need to define a variable newheadcur and newheadprev. The new linked list finds the corresponding insertion position by comparing the values
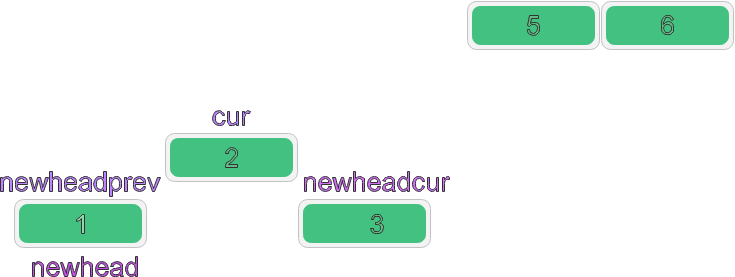
Just insert it
Case 3:
The corresponding value of the node where cur is located is larger than the value of the new linked list, which requires tail interpolation
Corresponding code:
class Solution {
public:
ListNode* insertionSortList(ListNode* head) {
if(!head||!head->next){//An empty node or only one node can be returned directly
return head;
}
ListNode*cur=head->next;//Traverse the remaining nodes
ListNode*newhead=head;
head->next=nullptr;//Remove the first node from the linked list
while(cur){
ListNode*next=cur->next;//Save next node
//Head insert
if(cur->val<newhead->val){
cur->next=newhead;
newhead=cur;
}else{
ListNode*newheadcur=newhead->next;
ListNode*newheadprev=newhead;
//Traverse the new linked list
while(newheadcur){
//Find insertion location
if(newheadcur->val>cur->val){
newheadprev->next=cur;//link
cur->next=newheadcur;
break;//Insert complete end loop
}else{
newheadprev=newheadcur;
newheadcur=newheadcur->next;
}
}
//Tail insertion
if(newheadcur==nullptr){
newheadprev->next=cur;
cur->next=nullptr;//Prevent ring formation
}
}
cur=next;
}
return newhead;
}
};Quick sort
Problem solving ideas:
Many old fellow may want to say how to sort lists quickly, and only to walk in the linked list can not go backward and how to use quick sort.
If you don't know, old fellow can go to see my sorting blog.
Specific steps:
We can select the head node as the benchmark value, traverse the linked list, and insert the smaller node head in front of it and the larger node tail behind it
Suppose smallHead maintains a header insertion pointer that is less than the reference value, and greaterHead maintains a tail insertion pointer that is greater than or equal to the reference value
Then there is a problem after the end of [head, end) fast platoon
-[smallHead, head] (closed left and open right) is a part less than the reference value
-[head - > next, end) (left closed and right open) is a part of the reference value greater than or equal to
Divide and conquer these two parts
Corresponding code:
class Solution {
public:
ListNode* sortList(ListNode* head) {
return quick_sortListNode(head,nullptr);
}
ListNode*quick_sortListNode(ListNode*head,ListNode*end){
if(head==end||head->next==end){
return head;//A node or no node can return head
}
ListNode*smallHead=head;
ListNode*greaterHead=head;
ListNode*cur=head->next;
int key=head->val;
//Select the first value as the key
while(cur!=end){
ListNode*next=cur->next;//Save the next node of cur
//Head insert
if(cur->val<key){
cur->next=smallHead;
smallHead=cur;
}else{
greaterHead->next=cur;
greaterHead=greaterHead->next;
}
cur=next;
}
greaterHead->next=end;//Link last node
//Recursive two parts
ListNode*ans=quick_sortListNode(smallHead,head);
head->next=quick_sortListNode(head->next,end);
return ans;
}
};Merge sort
Problem solving ideas:
Merge and sort, can't escape, open and close. The idea is as follows:
Split - > continuously split the linked list through recursion. In this process, you need to keep thinking about cutting the linked list without losing it (e.g. 8 - > 4 - > 2)
The key is to find the central point of the linked list and divide the linked list into two parts from the central point.
We can use the classic fast and slow double pointer linked list segmentation method. One thing to note is that the length of the linked list is odd and even, and the cutting processing methods are different. It can be processed according to the way you like. There is no clear provision on what cutting method must be used. The author's switching strategy is as follows:
The fast pointer moves 2 steps each time and the slow pointer moves 1} step each time. When the fast pointer reaches the end of the linked list, the linked list node pointed to by the slow pointer is the midpoint of the linked list.
After finding the midpoint, disconnect the linked list and divide the current linked list into two parts
Sort the two linked lists respectively. The next node of the slow pointer can point to null
End of segmentation phase - > recursive exit - > until the len gt h of the split linked list is 1. At this point, recursion to the end
In the merge phase, in the process of exiting recursion, the merge nodes are sorted and merged continuously. In fact, it is included in the segmentation phase. Merge - > sort the current linked list.
Corresponding split linked list code:
ListNode*splitListNode(ListNode*head){
if(!head||!head->next)return head;
ListNode*slow=head;
ListNode*fast=head;
ListNode*prev=nullptr;
while(fast&&fast->next){
prev=slow;
fast=fast->next->next;
slow=slow->next;
}
return prev;
}Note that the middle node should be assigned to the second segment of the split linked list
If there are only two nodes, slow points to the second node. If you assign it to the first merged linked list, it will be dead circulation!!!!
Corresponding code of consolidated linked list:
ListNode*mergeListNode(ListNode*head1,ListNode*head2){
ListNode*dummyHead=new ListNode(-1);
ListNode*ans=dummyHead;
while(head1&&head2){
if(head1->val<=head2->val){
ans->next=head1;
ans=ans->next;
head1=head1->next;
}
else{
ans->next=head2;
ans=ans->next;
head2=head2->next;
}
}
if(head1)ans->next=head1;
if(head2)ans->next=head2;
return dummyHead->next;
}The above operations are explained in the previous linked list blog. If the old fellow is not too clear, I can read my previous blog.
Total code:
class Solution {
public:
ListNode*splitListNode(ListNode*head){
if(!head||!head->next)return head;
ListNode*slow=head;
ListNode*fast=head;
ListNode*prev=nullptr;
while(fast&&fast->next){
prev=slow;
fast=fast->next->next;
slow=slow->next;
}
return prev;
}
ListNode*mergeListNode(ListNode*head1,ListNode*head2){
ListNode*dummyHead=new ListNode(-1);
ListNode*ans=dummyHead;
while(head1&&head2){
if(head1->val<=head2->val){
ans->next=head1;
ans=ans->next;
head1=head1->next;
}
else{
ans->next=head2;
ans=ans->next;
head2=head2->next;
}
}
if(head1)ans->next=head1;
if(head2)ans->next=head2;
return dummyHead->next;
}
ListNode* sortList(ListNode* head) {
if(!head||!head->next)return head;
ListNode*mid=splitListNode(head);
ListNode*midNext=mid->next;
mid->next=nullptr;
//Chemical linked list
ListNode*head1=sortList(head);
ListNode*head2= sortList(midNext);
return mergeListNode(head1,head2);
}
};Bubble sorting
Bubble sorting is relatively simple, and the code is directly given here:
Corresponding code:
void BubbleSort(struct Node* headNode)
{
struct Node* firstNode = headNode->next;
struct Node* secondNode = headNode;
while (firstNode != NULL)
{
while (firstNode->next != NULL)
{
if (firstNode->data > firstNode->next->data)
{
int temp = firstNode->data;
firstNode->data = firstNode->next->data;
firstNode->next->data = temp;
}
firstNode = firstNode->next;
}
//Reduce sorting times
firstNode = secondNode->next;
secondNode = firstNode;
}
}If you think the old iron can be a good old fellow,
