The sorting time complexity of bubbling, insertion and sorting is O(n2), which has high time complexity and is suitable for small-scale data processing.
For large-scale data sorting, merge sorting and quick sorting are more suitable.
Both merge sort and quick sort use the idea of divide and rule.
Merge sort
The idea of merging and sorting is to divide the array into two parts, and then divide the separated two parts into two parts, and so on, until they can't be divided, and then merge them together, so that the array can be orderly.
This first divides into two halves, then divides the two halves into two halves, and then divides into two halves. This is the recursive idea described earlier. So you can use recursion to complete merge sorting.
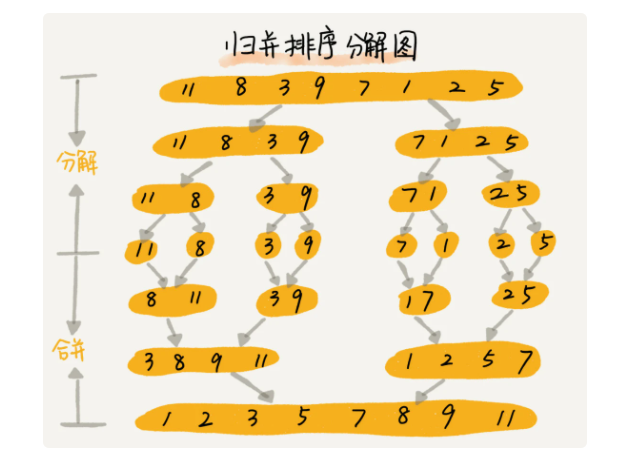
The idea of merging and sorting is to divide and rule, divide and rule, and divide big problems into small problems. When small problems are solved, big problems are also solved.
Divide and conquer is an idea to solve problems, and recursion is a programming skill. The two do not conflict.
Merge and sort with recursion:
1. Recursive formula
merge_ sort(p…r) = merge(merge_sort(p…q),merge_sort(q+1... r)), where q is the subscript of the intermediate element, representing half
2. Termination conditions:
p> = R
p. R is the initial coordinate and the last element coordinate of the unordered array. The whole sorting problem is transformed into two subproblems, one is merge_sort(p... q) and merge_sort(q+1…r). Use recursion to deal with sub problems. When the sub problems are handled well, merge them. In this way, the large data problems from P to R are also handled well.
The code is as follows:
public static void merge(int[] arr, int start, int mid,int end){
int i = start; //Left traversal starting point
int j = mid+1; //Right traversal starting point
int[] tmp = new int[end-start+1]; //Temporary array
int tmp_i = 0; //Temporary array start coordinates
while (i<=mid&&j<=end){ //The left side traverses from the starting point to mid, and the right side traverses from mid+1 to end. Both sides start traversing together
if (arr[i]<arr[j]){ //Put the small one into the array. If the right is larger than the left, put the small left into the temporary array first
tmp[tmp_i++] = arr[i++];//Put the small one on the left into the array
}else {
tmp[tmp_i++] = arr[j++]; //Put the small right into the array
}
}
while (i<=mid){ After the above traversal, there are still values on the left that have not been put into the array, so they can be put directly
tmp[tmp_i++] = arr[i++];
}
while (j<=end){After the above traversal, there are still values on the right that have not been put into the array, so they can be put directly
tmp[tmp_i++] = arr[j++];
}
for (i=0; i<tmp_i;++i){ //Traverse the temporary array and replace the original array
arr[start++] = tmp[i];
}
}
public static void merger_up_todown(int[] arr, int start, int end){
if (start<end){//Recursive end condition
int mid= (start+end)/2;
merger_up_todown(arr,start,mid); //Recursive left
merger_up_todown(arr,mid+1,end);//Recursive right
merge(arr,start,mid,end);//merge
}
}
Start with Mercer_ up_ In the todown method, three merge s are recursive,
The first two mergers_ up_ Todown splits the two halves of the array and combines them into ordered subarrays
The last merge combines the first two ordered sub arrays into an ordered array
The overall process is as follows:
1. Apply for a tmp temporary array with the same size as the unordered array arr.
2. Then apply that the two coordinates i and j represent the initial element i and the intermediate element + 1. Represents the starting point elements that divide the array into two halves, namely A[p... q] and A[q+1... r]
3. Compare two elements A[i] and A[j], which is smaller, put it into the temporary array tmp, and move I or j one bit later.
4. The third step above circulates until all arrays of a sub array are put into the temporary array, and then all the remaining elements of another array are put into the end of the temporary array in turn. At this time, the temporary array stores the final result of the merging of the two sub arrays, and then copies the data of the temporary array to the unordered array arr.

Performance analysis of merge sort
Is merge sort a stable sort algorithm
During the merging process, if there are elements with the same value between A[p... q] and A[q+1... r], first put the elements of A[p... q] into the temporary array, so the position of the same elements is not changed, so it is stable.
Merge sort time complexity
In the hypothetical merging sort, problem a is decomposed into solving problem b and problem c. after b and c are solved, b and c are merged
The time to solve a problem is T(a), and the time to solve B and C is T(b) and t (c)
that
T(1) =C ;C stands for constant time
(a) = T(b) + T© + K
K is the time to merge the two questions bc
Suppose T(n) of the merge sort time for n elements,
Then the time of two decomposition sub problems is T(n/2), and the time complexity of merging two ordered sub arrays is O(n)
Therefore, the calculation formula of merging time complexity is
T(n) = 2T(n/2) + n; n>1
Namely
T(n) = 2T(n/2) + n
= 2*(2T(n/4) + n/2) + n = 4T(n/4) + 2n
= 4(2T(n/8) + n/4) + 2n = 8T(n/8) + 3n
= 8*(2T(n/16) + n/8) + 3n = 16T(n/16) + 4n
...
= 2^k * T(n/2^k) + k * n
...
T(n) =2^k * T(n/2^k) + k * n.
When T(n/2^k)=T(1)
That is, n/2^k=1, so k=log2n. Bring K into the formula to get T(n)=Cn+nlog2n. Replace it with O (n), and t (n) is equal to O(nlogn)
Therefore, the time complexity of merge sorting is O(nlogn). The time complexity is stable, including the best, worst, and average time complexity of O(nlogn).
Spatial complexity
This is the weakness of merge sort. Merge sort is not in-situ sort.
Merge sort needs to use a temporary array tmp when sorting. The size of this array is the same as the original unordered array. Therefore, the space complexity is O(n).
Quick row
The core idea of quick sorting is divide and conquer. For example, to sort the data of the array of coordinates p to r, and then specify a point between p-r to be called partition point pivot, so that the number on the left of the partition point is smaller than that on the partition point, that is, arr [P] < arr [pivot], and the number on the right of the partition point is larger than that on the partition point, that is, arr [pivot] < arr [r], and then through recursion The divide and conquer idea reduces the distance from P to pivot and the distance from pivot to r, so that the interval becomes 1, and the data is orderly.
How to arrange data so that the number on the left is smaller than that on the partition point and the number on the right is larger than that on the partition point, there are usually three methods, as follows:
package com.company;
import java.util.Arrays;
public class MyquickSort {
public static void main(String[] args) {
int[] arr1 = {0,11111,103,100,1,3,2,6,4,5,8,7,10,9};
quecksort3(arr1,0,arr1.length-1);
System.out.println(Arrays.toString(arr1));
}
public static void quicksort1(int[] arr, int begin, int end){
//Left and right pointer method
/**
* 1.Select a key, usually the leftmost or rightmost
* 2.Define begin,end, begin from left to right, and end from right to left
* 3.key If it's on the left, go first. If key is on the right, go first
* 4.In the process of walking, if the number encountered by end is less than that encountered by key, stop. At this time, it is arr[end]
* 5.end After stopping, begin also moves forward. If it encounters a number greater than the key, it also stops. At this time, it is arr[begin]
* 6.arr[end]Exchange with arr[begin]
* 7.After the exchange, end continues to move to the left. If it is smaller than the number of key s, stop
* 8.begin Go to the right. If you encounter a number larger than key, stop and exchange.
* 9.If you do not encounter a number larger than key at the 8th, begin will encounter end. Is begin=end
* 10.At this time, exchange the number corresponding to the key and begin. After the exchange, the number on the left of the new key is smaller than the key, and the number on the right is larger than the key
* **/
if (begin >= end){
return;
}
/*
* begin,0, end arr.length-1
* */
int left = begin; //Define a left variable and leave it for recursion
int right = end; //Define a right variable and leave it for recursion
int keyi = begin; //Define the lower coordinate of the key.
while (begin < end){ //Traverse when begin < end, jump out of the loop when begin=end, and exchange with arr[begin] and arr[keyi]
while (arr[end] >= arr[keyi] && begin <end){ --end;} //Find the lower coordinate of arr [End] < arr [Keyi] when begin < end, that is, find a value smaller than key on the right
while (arr[begin] <= arr[keyi] && begin < end){ ++begin;}//In the same way, find a value larger than key on the left
int tmp = arr[end]; // These three lines exchange the large value arr[end] on the right and the small value arr[begin] on the left found above
arr[end] = arr[begin];
arr[begin]=tmp;
}
//After the above while loop, the begin and end pointers have met, that is, begin = end. Therefore, the value corresponding to the begin coordinate needs to be exchanged with the key value
int tmp = arr[end];
arr[end] = arr[keyi];
arr[keyi] = tmp;
keyi = end; //Assign the lower coordinates where begin and end meet to keyi as the data cutting point, cut the data on the left for the next recursion, and cut the data on the left for recursion
quicksort1(arr,left,keyi-1);
quicksort1(arr,keyi+1,right);
}
public static void quicksort2(int[] arr, int begin, int end){
//Excavation method
/**
* 1.Define a separate variable key to store the key value (the key value, not the lower coordinate), which is generally the leftmost or rightmost element of the array
* 2.1 After completion, the coordinate corresponding to the key value can be regarded as a pit position, which can be filled in with other numbers at will (i.e. assigned to the lower coordinate)
* 3.Define the 0 coordinate and the end coordinate of the array corresponding to the two pointers begin\end
* 4.If the leftmost (i.e. arr[begin], the lower coordinate of the array 0) is selected as the key value, that is, the pit position is arr[begin], because the value of arr[begin] has been assigned to the key and is not affected by the array, traverse from end -- first
* 5.If end -- traverses and finds arr[end] smaller than the key value, it is necessary to assign arr[end] to the pit position of 4, arr[begin] = arr[end], commonly known as pit filling. After the assignment and pit filling are completed, the arr[end] at this time will become a new pit position
* 6.end After filling the pit, start the begin + + traversal to find the value arr[begin] larger than the key, and then assign the value to the arr[end] pit of 5 to fill the pit. At this time, the arr[begin] becomes a new pit.
* 7.begin After filling the pit, repeat steps 5 and 6 until begin and end meet at a pit position (end/begin after filling the pit, the pit position is left at the end/begin position, and then the other pointer begin/end traverses + + / - - can't find a value larger or smaller than the key, and traverses until begin=end)
* 8.After meeting, the lower coordinate is the pit position. Assign the key value to the pit position,
* 9.Define the pit position to keyi, segment the data and recurse respectively
* */
if (begin>=end) {return;}
int left = begin;//Define a left variable and leave it for recursion
int right = end;//Define a right variable and leave it for recursion
int key = arr[begin]; //Define and assign the leftmost bit arr[0] of the array to the variable key, leaving the pit bit
while (begin<end){//Left and right pointer traversal
while (arr[end] >=key && begin < end){ --end; } //end find the value where the pointer is smaller than the key,
arr[begin] = arr[end]; //Assign the value smaller than the key found by end to the pit location arr[begin] to fill the pit, leaving the pit location arr[begin]
while (arr[begin] <= key && begin < end){++begin;}//end after filling the pit, begin + + finds a value greater than key,
arr[end] = arr[begin];//Assign the value found in begin to arr[begin] to fill the pit and leave the pit position
}
//begin and end meet in a pit
arr[begin] = key; //Pit filling with key
int keyi = begin; //The last pit position processed this time is used as the data cutting point to cut the data
quicksort2(arr,left,keyi-1);//Split data, left recursive
quicksort2(arr,keyi+1,right);//Split data, recursive on the right
}
public static void quecksort3(int[] arr, int begin, int end){
//Front and back pointer
/**
* 1.Select a key and record its lower coordinates with keyi, usually the rightmost or leftmost.
* 2.Before defining pre, point to the beginning of the array (at the beginning, pre points to begin-1), and cur pointer points to pre+1(begin)
* 3.First, arr[cur] will be compared with the key value arr[keyi]. If arr[cur] is smaller than the key value, the pre pointer will move back one bit, that is, pre+1. Then, arr[pre+1] will exchange data with arr[cur]. After the exchange, cur will continue to cur later++
* 4.If arr[cur] is greater than the key value, cur will go back all the time++
* 5.cur++Go straight back until cur reaches the end position, that is, cur=end
* 6.cur=end After that, the key value arr[keyi] is exchanged with the + + pre value arr[++pre],
* 7.Then, the left side of pre is a smaller number than it, and the right side is a larger number than it. Therefore, assign the pre at this time to keyi, segment the data, and recurse
* */
if (begin >= end){return;}
int pre = begin - 1,cur = begin;
int keyi = end;
while (cur != end){
System.out.println("pre:"+pre);
System.out.println("cur:"+cur);
System.out.println("stop");
if (arr[cur] < arr[keyi] && ++pre !=cur){
int tmp = arr[pre];
arr[pre] = arr[cur];
arr[cur] = tmp;
}
++cur;
}
int tmp1 = arr[keyi];
arr[keyi] = arr[++pre];
arr[pre] = tmp1;
keyi = pre;
quecksort3(arr,begin,keyi-1);
quecksort3(arr,keyi+1,end);
}
}
Merge sort contrast quick sort
Merge sort and fast sort are realized by using the idea of divide and conquer and recursion. To understand merge sort, it is important to understand recursive formula and merge() merge function. To understand fast sort, it is important to understand recursive formula and partition() method.
Merge sort is a sort method with relatively stable time complexity. The disadvantage is whether it is sorted in place, high spatial complexity and O(N)
The worst time complexity of fast scheduling is O(n2), but the average complexity is O(nlogn). And very small probability evolves into the worst time complexity.