Quick sort

Quick sort is an improvement of bubble sort. Its basic idea is to divide the data to be sorted into two independent parts through one-time sorting. All the data in one part is smaller than all the data in the other part, and then quickly sort the two parts of data according to this method. The whole sorting process can be recursive, so as to turn the whole data into an ordered sequence.

Requirements:

Before sorting: {6, 1, 2, 7, 9, 3, 4, 5, 8}

After sorting: {1, 2, 3, 4, 5, 6, 7, 8, 9}

Sorting principle:

1. First, set a boundary value, and divide the array into left and right parts through the boundary value;

2. Put the data greater than or equal to the boundary value to the right of the array, and the data less than the boundary value to the left of the array. At this time, all elements in the left part are less than or equal to the boundary value, while all elements in the right part are greater than or equal to the boundary value;

3. Then, the data on the left and right can be sorted independently. For the array data on the left, you can take another boundary value and divide this part of the data into left and right parts. Similarly, place the smaller value on the left and the larger value on the right. The array data on the right can also be processed similarly.

4. By repeating the above process, it can be seen that this is a recursive definition. After the left part is sorted recursively, the right part is sorted recursively. When the data of the left and right parts are sorted, the sorting of the whole array is completed.

Quicksort API design:

Class name	Quick
Construction method	Quick(): create a quick object
Member method	1.public static void sort(Comparable[] a): sort the elements in the array 2.private static void sort(Comparable[] a, int lo, int hi): sort the elements in array a from index lo to index hi 3.public static int partition(Comparable[] a,int lo,int hi): groups the elements in array a from index lo to index hi, and returns the index corresponding to the grouping boundary 4.private static boolean less(Comparable v,Comparable w): judge whether v is less than W 5.private static void exch(Comparable[] a,int i,int j): exchange the values at index I and index J in array a

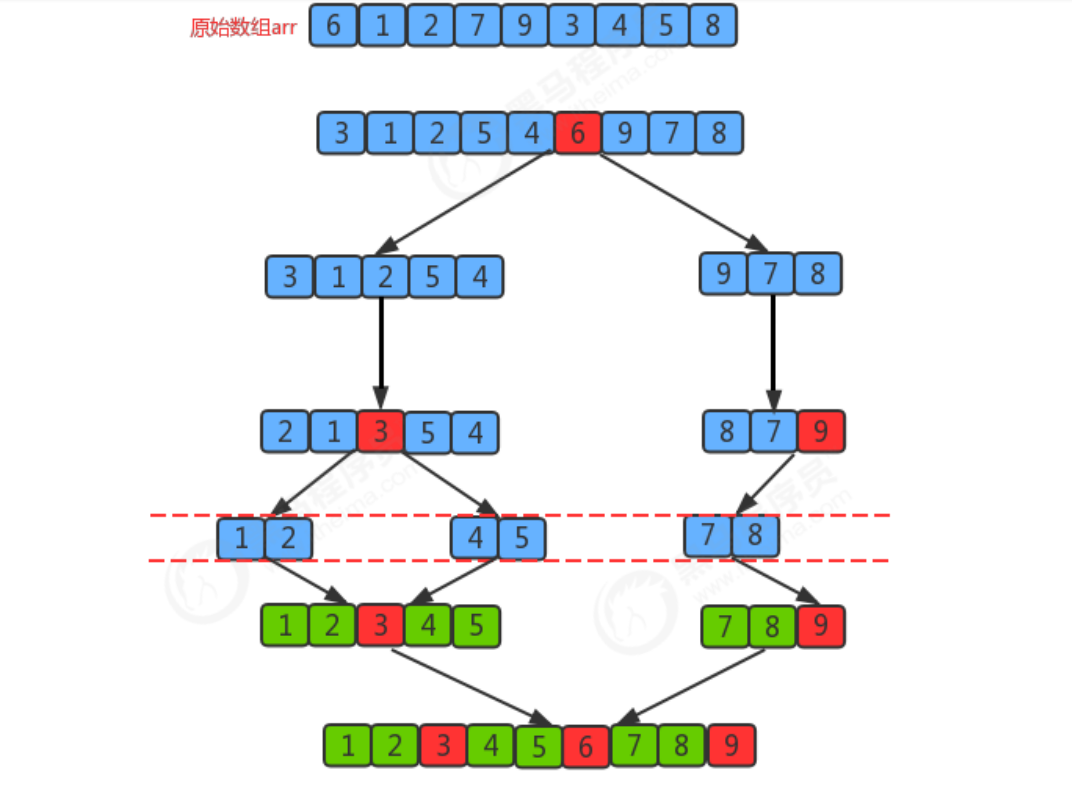
Segmentation principle:

The basic idea of dividing an array into two subarrays:

1. Find a reference value and point to the head and tail of the array with two pointers respectively;

2. Search for an element smaller than the reference value from the tail to the head, stop the search, and record the position of the pointer;

3. Search for an element larger than the reference value from the head to the tail, stop the search, and record the position of the pointer;

4. Exchange the elements of the current left pointer position and the right pointer position;

5. Repeat steps 2, 3 and 4 until the value of the left pointer is greater than that of the right pointer.

Quick sort code implementation:

/**
 * Quick sort -- time complexity O(nlogn)
 */
public class Quick {

    /* Sort the elements in the array */
    public static void sort(Comparable[] a) {
        int lo = 0;
        int hi = a.length - 1;
        sort(a, lo, hi);
    }

    /* Sort the elements in array a from index lo to index hi */
    private static void sort(Comparable[] a, int lo, int hi) {
        // Robustness judgment
        if (lo >= hi) {
            return;
        }
        // Split: split the elements from lo to hi in the a array
        int partition = partition(a, lo, hi);
        // Rule: sort the elements in the left group (recursively call sort)
        sort(a, lo, partition - 1);
        // Sort the elements in the right group (recursively call sort)
        sort(a, partition + 1, hi);
    }

    /* Group the elements in array a from index lo to index hi, and return the index corresponding to the grouping boundary (the index after grouping changes) */
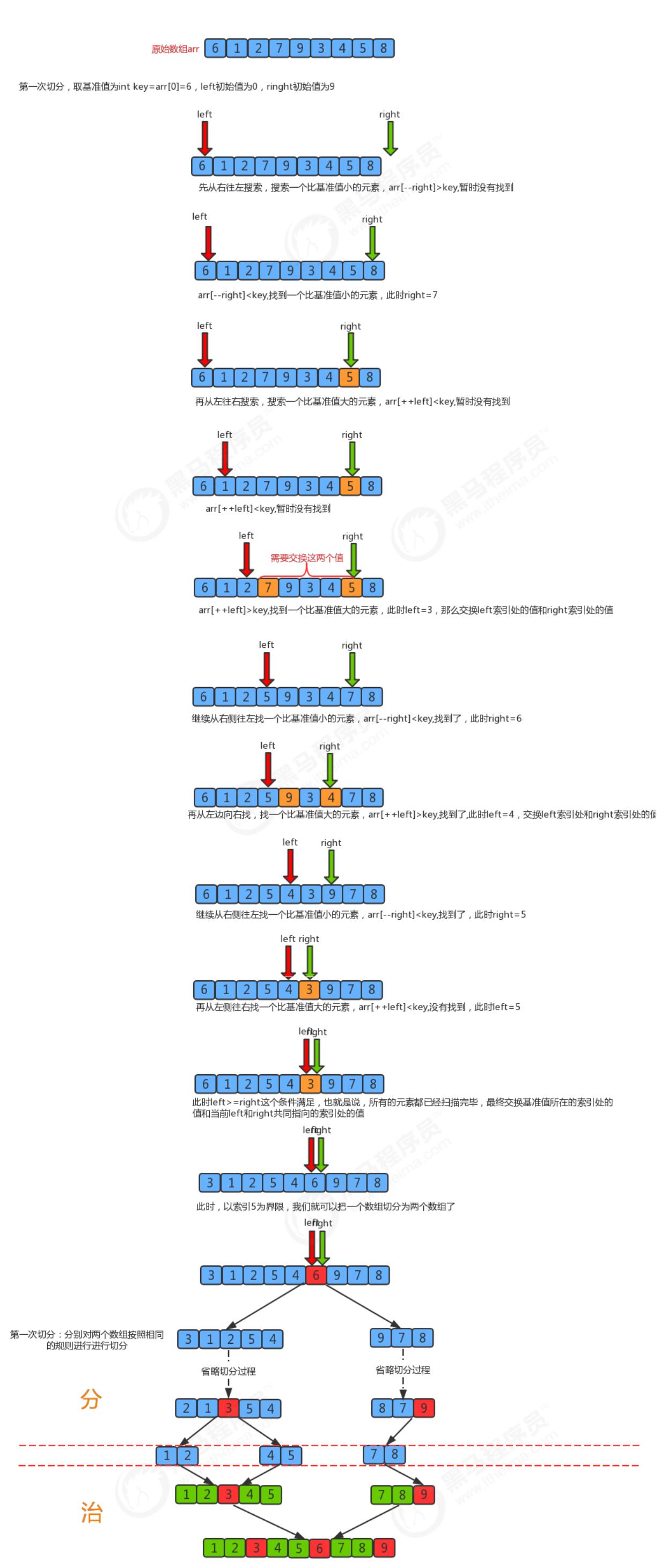
    public static int partition(Comparable[] a, int lo, int hi) {
        Comparable key = a[lo]; // Take the leftmost element as the reference value
        int left = lo; // Defines a left pointer that initially points to the leftmost element
        int right = hi + 1; // Define a right pointer that initially points to the next position of the left and right elements
        //Perform segmentation
        while (true) {
            // Scan from right to left to find an element smaller than the reference value
            while (less(key, a[--right])) { // The loop stops, proving that an element smaller than the reference value is found
                if (right == lo) {
                    break; // It has been scanned to the far left. There is no need to continue scanning
                }
            }
            // Then scan from left to right to find an element larger than the reference value
            while (less(a[++left], key)) { // The loop stops, proving that an element larger than the reference value is found
                if (left == hi) { // It has been scanned to the far right. There is no need to continue scanning
                    break;
                }
            }
            // All elements are scanned and the loop ends
            if (left >= right) {
                break;
            } else {
                exchange(a, left, right);
            }
        }

        //Swap the values at the last right index and the index where the reference value is located
        exchange(a, lo, right);
        return right;
    }


    /* Array elements i and j swap positions */
    private static void exchange(Comparable[] a, int i, int j) {
        Comparable temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

    /* Compare whether the v element is smaller than the w element */
    private static boolean less(Comparable v, Comparable w) {
        return v.compareTo(w) < 0;
    }
}

Difference between quick sort and merge sort:

Quick sort is another divide and conquer sorting algorithm. It divides an array into two sub arrays and sorts the two parts independently. Quick sort and merge sort are complementary: merge sort divides the array into two sub arrays, sorts them respectively, and merges the ordered sub arrays to sort the whole array. The way of quick sort is that when the two arrays are ordered, the whole array is naturally ordered. In merge sort, an array is equally divided into two parts. The merge call occurs before processing the whole array. In quick sort, the position of the split array depends on the content of the array, and the recursive call occurs after processing the whole array.

Quick sort time complexity analysis:

The first segmentation of quick sort starts from both ends and searches alternately until left and right coincide. Therefore, the time complexity of the first segmentation algorithm is O(n), but the time complexity of the whole quick sort is related to the number of segmentation.

Optimal situation: the benchmark number selected for each segmentation just divides the current sequence equally.

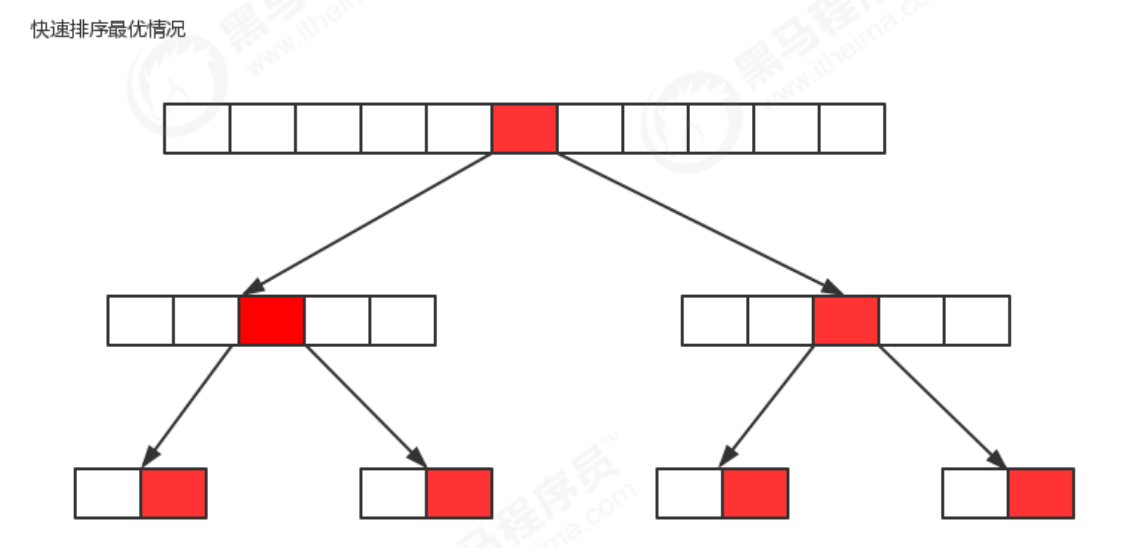
If we regard the segmentation of an array as a tree, the above figure is the diagram of its optimal situation, which has been segmented logn times. Therefore, the time complexity of quick sorting in the optimal situation is O(nlogn);

Worst case: the benchmark number selected for each segmentation is the maximum number or the minimum number in the current sequence, so that each segmentation will have a subgroup, so it will be segmented n times in total. Therefore, in the worst case, the time complexity of quick sorting is O(n^2);

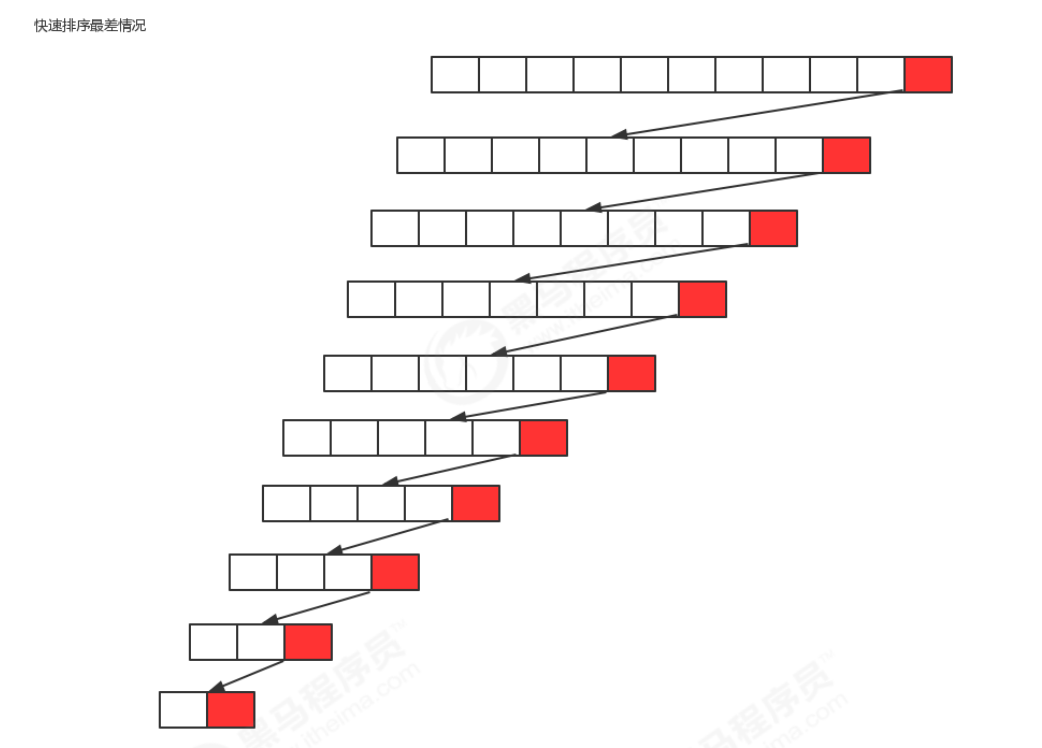
Average situation: the benchmark number selected for each segmentation is neither the maximum value, the minimum value nor the median value. In this case, we can also prove by mathematical induction that the time complexity of quick sorting is O(nlogn)