I Linear regression
1. lm() function returns the prediction model of input variables, and the returned results can be used with many functions.
> lm.model <- lm(wt ~ mpg, data = mtcars)
> coefficients(lm.model) # Extraction coefficient
(Intercept) mpg
6.047255 -0.140862
> confint(lm.model, level=0.95) # After the distribution of the correlation coefficient of the linear model is obtained, the interval is limited to obtain the value of the boundary point
2.5 % 97.5 %
(Intercept) 5.4168245 6.6776856
mpg -0.1709569 -0.1107671
> fitted(lm.model) # Use the established model to predict wt
Mazda RX4 Mazda RX4 Wag Datsun 710 Hornet 4 Drive Hornet Sportabout Valiant Duster 360
3.089154 3.089154 2.835602 3.032809 3.413136 3.497653 4.032929
Merc 240D Merc 230 Merc 280 Merc 280C Merc 450SE Merc 450SL Merc 450SLC
2.610223 2.835602 3.342705 3.539912 3.737119 3.610343 3.906153
Cadillac Fleetwood Lincoln Continental Chrysler Imperial Fiat 128 Honda Civic Toyota Corolla Toyota Corona
4.582291 4.582291 3.976584 1.483327 1.765051 1.272034 3.018723
Dodge Challenger AMC Javelin Camaro Z28 Pontiac Firebird Fiat X1-9 Porsche 914-2 Lotus Europa
3.863894 3.906153 4.173791 3.342705 2.201723 2.384844 1.765051
Ford Pantera L Ferrari Dino Maserati Bora Volvo 142E
3.821636 3.272274 3.934325 3.032809
> residuals(lm.model) # Residual between prediction and reality
Mazda RX4 Mazda RX4 Wag Datsun 710 Hornet 4 Drive Hornet Sportabout Valiant Duster 360
-0.46915365 -0.21415365 -0.51560210 0.18219114 0.02686382 -0.03765336 -0.46292884
Merc 240D Merc 230 Merc 280 Merc 280C Merc 450SE Merc 450SL Merc 450SLC
0.57977705 0.31439790 0.09729481 -0.09991195 0.33288129 0.11965707 -0.12615307
Cadillac Fleetwood Lincoln Continental Chrysler Imperial Fiat 128 Honda Civic Toyota Corolla Toyota Corona
0.66770947 0.84170947 1.36841594 0.71667281 -0.15005113 0.56296577 -0.55372266
Dodge Challenger AMC Javelin Camaro Z28 Pontiac Firebird Fiat X1-9 Porsche 914-2 Lotus Europa
-0.34389448 -0.47115307 -0.33379081 0.50229481 -0.26672324 -0.24484380 -0.25205113
Ford Pantera L Ferrari Dino Maserati Bora Volvo 142E
-0.65163589 -0.50227421 -0.36432547 -0.25280886
> anova(lm.model) # anova table
Analysis of Variance Table
Response: wt
Df Sum Sq Mean Sq F value Pr(>F)
mpg 1 22.3431 22.3431 91.375 1.294e-10 ***
Residuals 30 7.3356 0.2445
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
> vcov(lm.model) # covariance matrix
(Intercept) mpg
(Intercept) 0.095289963 -0.0043626666
mpg -0.004362667 0.0002171494
> influence(lm.model) # It is equivalent to a summary of the results of the analysis
$hat
Mazda RX4 Mazda RX4 Wag Datsun 710 Hornet 4 Drive Hornet Sportabout Valiant Duster 360
0.03198439 0.03198439 0.03776901 0.03277255 0.03296737 0.03476902 0.06102792
Merc 240D Merc 230 Merc 280 Merc 280C Merc 450SE Merc 450SL Merc 450SLC
0.04774195 0.03776901 0.03195442 0.03590963 0.04334604 0.03816586 0.05249086
Cadillac Fleetwood Lincoln Continental Chrysler Imperial Fiat 128 Honda Civic Toyota Corolla Toyota Corona
0.11464634 0.11464634 0.05705606 0.16580983 0.12563611 0.20060244 0.03301399
Dodge Challenger AMC Javelin Camaro Z28 Pontiac Firebird Fiat X1-9 Porsche 914-2 Lotus Europa
0.04996488 0.05249086 0.07220085 0.03195442 0.07740711 0.06226177 0.12563611
Ford Pantera L Ferrari Dino Maserati Bora Volvo 142E
0.04759875 0.03138551 0.05426366 0.03277255
$coefficients
(Intercept) mpg
Mazda RX4 -0.007282030 -3.913985e-04
Mazda RX4 Wag -0.003324014 -1.786609e-04
Datsun 710 0.009157470 -1.289282e-03
Hornet 4 Drive 0.001485910 2.190313e-04
Hornet Sportabout 0.001557359 -3.430679e-05
Valiant -0.002604528 6.896128e-05
Duster 360 -0.066342655 2.535306e-03
Merc 240D -0.027785644 2.330044e-03
Merc 230 -0.005583936 7.861634e-04
Merc 280 0.004737902 -7.949360e-05
Merc 280C -0.007473905 2.108129e-04
Merc 450SE 0.033786317 -1.140454e-03
Merc 450SL 0.010081735 -3.083068e-04
Merc 450SLC -0.015778260 5.782587e-04
Cadillac Fleetwood 0.153962430 -6.490318e-03
Lincoln Continental 0.194083866 -8.181645e-03
Chrysler Imperial 0.184925710 -6.947280e-03
Fiat 128 -0.161833613 9.391507e-03
Honda Civic 0.026202892 -1.571169e-03
Toyota Corolla -0.151504789 8.636477e-03
Toyota Corona -0.003495500 -7.167077e-04
Dodge Challenger -0.040959820 1.475709e-03
AMC Javelin -0.058928219 2.159665e-03
Camaro Z28 -0.054830702 2.169570e-03
Pontiac Firebird 0.024459924 -4.103942e-04
Fiat X1-9 0.028152063 -1.850938e-03
Porsche 914-2 0.019369325 -1.370227e-03
Lotus Europa 0.044014788 -2.639199e-03
Ford Pantera L -0.073758568 2.607048e-03
Ferrari Dino -0.019818649 1.798843e-04
Maserati Bora -0.047027088 1.741542e-03
Volvo 142E -0.002061852 -3.039283e-04
$sigma
Mazda RX4 Mazda RX4 Wag Datsun 710 Hornet 4 Drive Hornet Sportabout Valiant Duster 360
0.4950874 0.5013168 0.4933815 0.5017657 0.5029179 0.5028932 0.4950577
Merc 240D Merc 230 Merc 280 Merc 280C Merc 450SE Merc 450SL Merc 450SLC
0.4906934 0.4994096 0.5026082 0.5025884 0.4989569 0.5024330 0.5023674
Cadillac Fleetwood Lincoln Continental Chrysler Imperial Fiat 128 Honda Civic Toyota Corolla Toyota Corona
0.4853738 0.4747194 0.4295043 0.4813738 0.5020600 0.4891637 0.4919538
Dodge Challenger AMC Javelin Camaro Z28 Pontiac Firebird Fiat X1-9 Porsche 914-2 Lotus Europa
0.4986579 0.4948469 0.4988098 0.4939281 0.5002931 0.5007472 0.5004465
Ford Pantera L Ferrari Dino Maserati Bora Volvo 142E
0.4874197 0.4939342 0.4981090 0.5006732
$wt.res
Mazda RX4 Mazda RX4 Wag Datsun 710 Hornet 4 Drive Hornet Sportabout Valiant Duster 360
-0.46915365 -0.21415365 -0.51560210 0.18219114 0.02686382 -0.03765336 -0.46292884
Merc 240D Merc 230 Merc 280 Merc 280C Merc 450SE Merc 450SL Merc 450SLC
0.57977705 0.31439790 0.09729481 -0.09991195 0.33288129 0.11965707 -0.12615307
Cadillac Fleetwood Lincoln Continental Chrysler Imperial Fiat 128 Honda Civic Toyota Corolla Toyota Corona
0.66770947 0.84170947 1.36841594 0.71667281 -0.15005113 0.56296577 -0.55372266
Dodge Challenger AMC Javelin Camaro Z28 Pontiac Firebird Fiat X1-9 Porsche 914-2 Lotus Europa
-0.34389448 -0.47115307 -0.33379081 0.50229481 -0.26672324 -0.24484380 -0.25205113
Ford Pantera L Ferrari Dino Maserati Bora Volvo 142E
-0.65163589 -0.50227421 -0.36432547 -0.252808862. Evaluation of fitting quality
(1) The predicted value is obtained according to the model
predict(model, For training generation model Data set of)
(2) Use the R2 function in the caret package
R2(predict As a result, in the original dataset y value)
II multiple linear regression
1. Analysis of LM () and interaction
(1) Directly enter multiple variables into fomular and connect them with a plus sign:
mtcars.m <- lm(wt~mpg+disp+mpg:disp, data = mtcars) ##Analyze the model of independent variable disp and mpg to dependent variable wt, where mpg:disp means that the interaction between the two variables is considered when constructing the linear model ##That is, the two variables are not independent of each other summary(mtcars.m)
Model:
> summary(mtcars.m)
Call:
lm(formula = wt ~ mpg + disp + mpg:disp, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-0.8047 -0.2636 0.0539 0.2340 0.8817
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.3716803 0.7066020 4.772 5.18e-05 ***
mpg -0.0505361 0.0257971 -1.959 0.06014 .
disp 0.0065258 0.0020525 3.179 0.00359 **
mpg:disp -0.0001603 0.0001232 -1.301 0.20383
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4055 on 28 degrees of freedom
Multiple R-squared: 0.8449, Adjusted R-squared: 0.8283
F-statistic: 50.84 on 3 and 28 DF, p-value: 1.871e-11
(2) influence weight of independent variable
Count the "importance" of different variables to the model:
library(relaimpo); calc.relimp( wt~mpg+disp+mpg:disp, data = mtcars )
> calc.relimp( wt~mpg+disp+mpg:disp, data = mtcars )
Response variable: wt
Total response variance: 0.957379
Analysis based on 32 observations
3 Regressors:
mpg disp mpg:disp
Proportion of variance explained by model: 84.49%
Metrics are not normalized (rela=FALSE).
Relative importance metrics: ##Influence weight
lmg
mpg 0.399914296
disp 0.435589844
mpg:disp 0.009378141
Average coefficients for different model sizes:
1X 2Xs 3Xs
mpg -0.140861970 -0.066315339 -0.0505361268
disp 0.007010325 0.004277131 0.0065257929
mpg:disp NaN NaN -0.0001603097(3) Visualize how independent variables affect each other
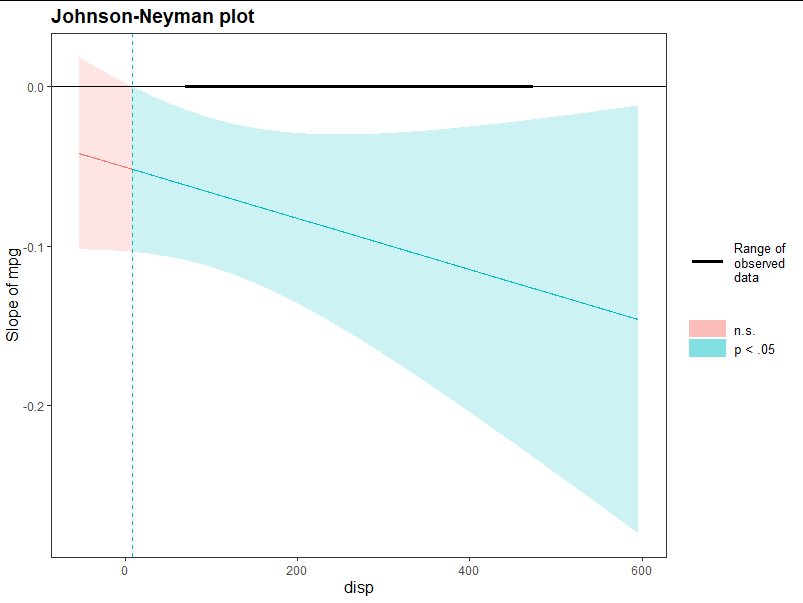
The interaction is mainly reflected in the change of slope:
library(interactions) sim_slopes(mtcars.m, pred = mpg, modx = disp, jnplot = TRUE) ##pred input affected amount modx input affected amount
Results:
JOHNSON-NEYMAN INTERVAL When disp is INSIDE the interval [8.39, 747.98], the slope of mpg is p < .05. Note: The range of observed values of disp is [71.10, 472.00] SIMPLE SLOPES ANALYSIS ##Random access to data, the results are somewhat outrageous
2. glm()
When the parameter famil y = "Gaussian" in glm function, your fitting effect is consistent with lm(), but glm can also be used in other regression models, such as linear regression in binary classification:
##glm is used to establish a linear model for the variables in swiss. When different independent variables are input, we can judge the corresponding specifications type through the numerical results
dat <- iris %>% filter( Species %in% c("setosa", "virginica") )
dat$Species <- as.factor(dat$Species)##The column corresponding to "dependent variable" needs to be processed, otherwise an error may be reported
bm <- glm( Species ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width,
data = dat, family = binomial ) ##Select the model of binomial distribution
mtcars.predict1 <- predict(bm, dat,type = "response")
mtcars.predict2 <- predict(bm, dat) ##Use the default typeResults: note that the response model is set, and the output value has the effect of binary classification
> mtcars.predict1
1 2 3 4 5 6 7 8 9 10 11 12
2.220446e-16 4.732528e-13 1.369834e-13 3.388726e-12 2.220446e-16 3.892826e-13 7.748530e-13 1.988060e-13 5.204109e-12 3.900993e-13 2.220446e-16 1.453927e-12
13 14 15 16 17 18 19 20 21 22 23 24
2.656364e-13 2.220446e-16 2.220446e-16 2.220446e-16 2.220446e-16 2.220446e-16 2.220446e-16 2.220446e-16 4.472442e-13 2.682276e-13 2.220446e-16 4.132652e-11
25 26 27 28 29 30 31 32 33 34 35 36
5.282004e-11 3.493413e-12 4.614812e-12 2.220446e-16 2.220446e-16 4.976501e-12 5.082694e-12 2.857677e-13 2.220446e-16 2.220446e-16 1.032749e-12 2.220446e-16
37 38 39 40 41 42 43 44 45 46 47 48
2.220446e-16 2.220446e-16 1.035326e-12 1.337875e-13 2.220446e-16 3.421128e-11 4.494793e-13 2.131127e-11 2.126479e-11 1.861773e-12 2.220446e-16 6.741667e-13
49 50 51 52 53 54 55 56 57 58 59 60
2.220446e-16 2.220446e-16 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
61 62 63 64 65 66 67 68 69 70 71 72
1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
73 74 75 76 77 78 79 80 81 82 83 84
1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
85 86 87 88 89 90 91 92 93 94 95 96
1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
97 98 99 100
1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
> mtcars.predict2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
-31.25726 -28.37915 -29.61892 -26.41057 -31.27837 -28.57447 -27.88610 -29.24645 -25.98157 -28.57237 -32.08233 -27.25675 -28.95665 -30.56889 -38.51083
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
-34.24374 -33.36463 -30.28368 -30.31909 -30.33771 -28.43567 -28.94694 -34.48423 -23.90952 -23.66413 -26.38014 -26.10175 -30.45579 -31.23614 -26.02629
31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
-26.00518 -28.88360 -33.93252 -35.76190 -27.59880 -32.00469 -34.03910 -31.85587 -27.59630 -29.64252 -31.08514 -24.09847 -28.43069 -24.57178 -24.57397
46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
-27.00949 -30.11375 -28.02530 -31.68625 -30.02680 42.30338 30.16757 35.29448 32.36693 37.44698 41.69689 25.43424 36.78895 34.84647 38.68465
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
26.28266 30.18619 31.69255 31.17407 34.61827 31.99455 29.96005 40.13440 48.50935 26.36952 34.80433 29.12103 42.35915 24.81853 33.23214
76 77 78 79 80 81 82 83 84 85 86 87 88 89 90
32.34083 23.59987 24.35911 35.30878 28.83298 35.38856 33.80247 36.28236 23.87569 30.51635 37.26026 36.12244 29.93893 23.55764 29.68174
91 92 93 94 95 96 97 98 99 100
35.78971 28.03628 30.16757 37.59549 37.12645 30.44316 27.82403 28.31458 33.14986 27.54634 III Multiple nonlinear regression
1. Machine learning -- regression analysis
(1) The data were analyzed using earth and caret toolkits
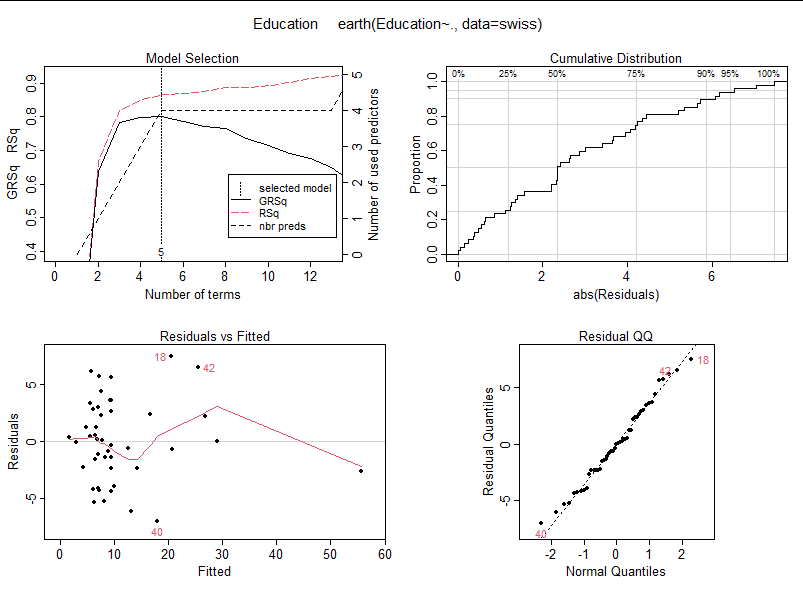
For example, regression analysis of Education for all other elements in swiss;
nls.model <- earth(Education~.,data = swiss) nls.model plot(nls.model)
(2) Adjust the parameters of the results (training)
Take n-Fold cross validation as an example, use the train function in the caret package:
train(x, y, method = "rf", preProcess = NULL, ...,
weights = NULL, metric = ifelse(is.factor(y), "Accuracy", "RMSE"),
maximize = ifelse(metric %in% c("RMSE", "logLoss", "MAE"), FALSE, TRUE),
trControl = trainControl(), tuneGrid = NULL,
tuneLength = ifelse(trControl$method == "none", 1, 3))Of which:
x: Input independent variable during fitting
y: Dependent variable input during fitting
Weights: the weights set according to the model are unnecessary
trControl: you need to call the result returned from trainControl() to design an appropriate inspection method
tuneGrid: the method applied in parameter adjustment. Different methods have different parameter adjustment methods, so the column names of the input grid are also different (the function controls parameter adjustment by identifying the column names of the input columns)
For example, a fitting function is established for the Fertility of swiss, and the dependent variable is all other columns:
grid <- expand.grid( degree = 1:3, nprune = seq(2, 100, length.out = 8) ) ##For a parameter adjustment grid specially constructed by method, degree represents the iteration depth and nprune represents the feature selection quantity ##expand. The grid function will adaptively generate the grid according to rows and columns to meet the matching relationship between data set.seed(12222)##Generating random seeds ensures the repeatability of the model swiss.model1 <- train( x = subset(swiss, select = -Fertility), y = swiss$Fertility, method = "earth", metric = "RMSE", trControl = trainControl(method = "cv", number = 10), ## 10% off cross validation tuneGrid = grid )
result:
> grid degree nprune 1 1 2 2 2 2 3 3 2 4 1 16 5 2 16 6 3 16 7 1 30 8 2 30 9 3 30 10 1 44 11 2 44 12 3 44 13 1 58 14 2 58 15 3 58 16 1 72 17 2 72 18 3 72 19 1 86 20 2 86 21 3 86 22 1 100 23 2 100 24 3 100
> swiss.model1 Multivariate Adaptive Regression Spline 47 samples 5 predictor No pre-processing Resampling: Cross-Validated (10 fold) Summary of sample sizes: 42, 42, 42, 42, 42, 44, ... Resampling results across tuning parameters: degree nprune RMSE Rsquared MAE 1 2 11.278358 0.3284905 9.209832 1 16 9.541177 0.5068536 7.839405 1 30 9.541177 0.5068536 7.839405 1 44 9.541177 0.5068536 7.839405 1 58 9.541177 0.5068536 7.839405 1 72 9.541177 0.5068536 7.839405 1 86 9.541177 0.5068536 7.839405 1 100 9.541177 0.5068536 7.839405 2 2 11.294113 0.3270052 9.216748 2 16 10.717470 0.4382987 8.802805 2 30 10.717470 0.4382987 8.802805 2 44 10.717470 0.4382987 8.802805 2 58 10.717470 0.4382987 8.802805 2 72 10.717470 0.4382987 8.802805 2 86 10.717470 0.4382987 8.802805 2 100 10.717470 0.4382987 8.802805 3 2 11.294113 0.3270052 9.216748 3 16 10.798077 0.4366048 8.891187 3 30 10.798077 0.4366048 8.891187 3 44 10.798077 0.4366048 8.891187 3 58 10.798077 0.4366048 8.891187 3 72 10.798077 0.4366048 8.891187 3 86 10.798077 0.4366048 8.891187 3 100 10.798077 0.4366048 8.891187 RMSE was used to select the optimal model using the smallest value. The final values used for the model were nprune = 16 and degree = 1.
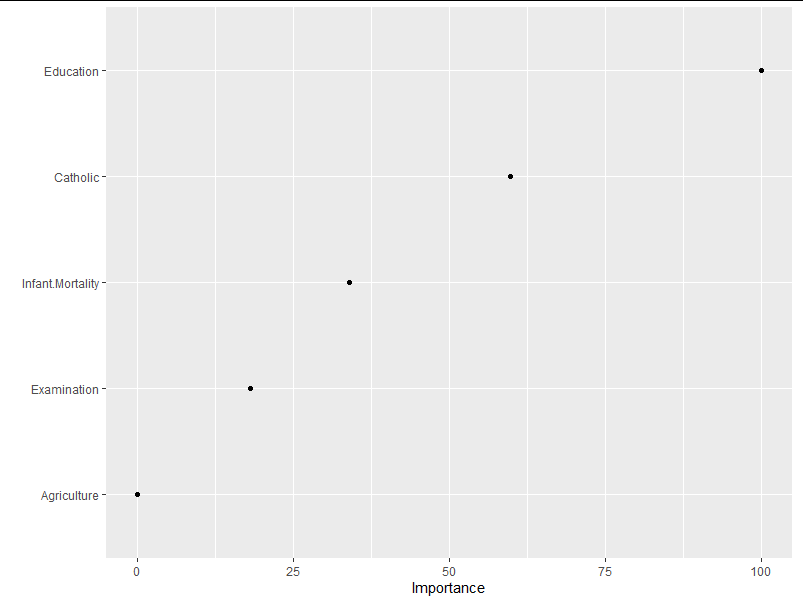
(3) vip is used to show the importance of different independent variables in the result model
library(vip); p1 <- vip(swiss.model1, num_features = 4, geom = "point", value = "gcv")
Where num_features controls the number of variables to be displayed (priority is given to those with significant influence). value is an indicator of quantitative importance, "gcv" means "Generalized cross − validation". You can also enter "rss" to measure importance by Residual Sums of Squares.
2. Logistic regression
> m <- drm(cyl ~ wt, fct = L.3(), data = mtcars) > plot(m, log="", main = "Logistic function") ##For example, natural data do not fit the logistic regression curve
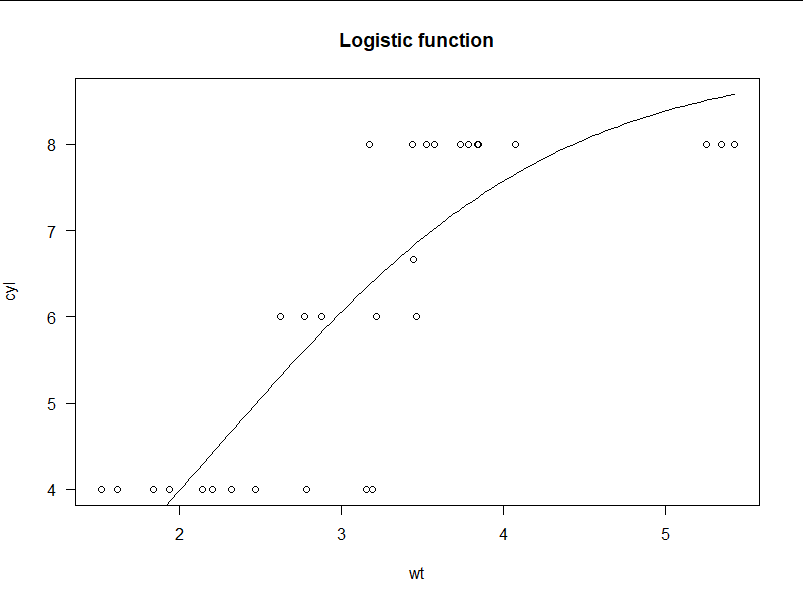
3. Nonlinear least square method
(1) Use nls function
nls(formula, data, start, control, algorithm,
trace, subset, weights, na.action, model,
lower, upper, ...)Formula: the formula needs to know the regression model in advance, and the function is only to fit the appropriate parameters
start: it can be a list that records the initial values of various parameters in a model function that cannot be started by itself
Control: a control of fitting conditions
set.seed(43247)
x<-seq(0, 100, 1)
y<-(rnorm(1,0,1)*x^2+runif(1,0,1)*x^3 +rnorm(101,0,1))
m<-nls(y~(a*x^2+b*x^3),
control = nls.control(maxiter = 100000), ##Control the maximum number of iterations
start = list(a=1, b=1));
result:
> m
Nonlinear regression model
model: y ~ (a * x^2 + b * x^3)
data: parent.frame()
a b
-0.7908 0.3721
residual sum-of-squares: 87.8
Number of iterations to convergence: 1
Achieved convergence tolerance: 5.332e-09(2) Automatic fitting using drm function
There is no need to know the function form in advance, only select the model with input, and adaptively start the fitting
library(drc)
m <- drm( y ~ x, fct = LL.3() ); ## Built in model
dat = data.frame(x=x,y=y,nls=predict(m)) ##When predict only inputs the model, it is equivalent to getting a function file
ggplot( dat,aes(x=x,y=y) ) +
geom_point() + geom_line( aes(x = x, y = nls), colour = "red");
'''
##fct: a list with three or more elements specifying the non-linear function, the accompanying self starter function, the names of the parameter in the non-linear function and, optionally, the first and second derivatives as well as information used for calculation of ED values. Currently available functions include, among others, the four- and five-parameter log-logistic models LL.4, LL.5 and the Weibull model W1.4. Use getMeanFunctions for a full list.
LL.3:
LL.3(fixed = c(NA, NA, NA), names = c("b", "d", "e"), ...)
f(x) = 0 + \frac{d-0}{1+\exp(b(\log(x)-\log(e)))}
'''