Record of sword finger offer (1) (February 18, 2022)
Write in the front: I haven't learned c + +. Refer to the problem-solving comments and learn while brushing the questions.
data structure
- Print linked list from end to end
describe
Enter the head node of a linked list and return the value of each node in the order from the end to the head of the linked list (returned with an array).
For example, enter the linked list of {1,2,3}
Returns an array of [3,2,1]
0 < = linked list length < = 10000
Solution: direct traversal
The topic is very simple and simple. We directly start from the head node of the linked list. Then we record the information of each node of the array. Finally, reverse the entire array and return.
The code is as follows
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) :
* val(x), next(NULL) {
* }
* };
*/
class Solution {
public:
vector<int> printListFromTailToHead(ListNode* head) {
vector<int> ans;
while(head){
ans.push_back(head->val);
head=head->next;
}
reverse(ans.begin(), ans.end());
return ans;
}
};
The length of direct traversal is n The time complexity of all nodes of the linked list is O(n)
The required storage length is n The spatial complexity of the linked list is all nodes O(n)
- Reverse linked list
describe
Given the head node phead of a single linked list (the head node has a value, for example, in the figure below, its val is 1) and the length is n, after reversing the linked list, return to the header of the new linked list.
Data range: 0 ≤ n ≤ 1000
Requirements: space complexity O(1)O(1), time complexity O(n)O(n).
For example, when the linked list {1,2,3} is entered,
After inversion, the original linked list becomes {3,2,1}, so the corresponding output is {3,2,1}.
What this question wants to investigate is: how to adjust the pointer of the linked list to achieve the purpose of reversing the linked list.
Initialization: 3 pointers
1)pre The pointer points to the last node of the inverted linked list. There is no inversion at the beginning, so it points to nullptr
2)cur The pointer points to the first node of the linked list to be reversed. At the beginning, the first node to be reversed, so it points to head
3)nex The pointer points to the second node of the linked list to be reversed. The purpose is to save the linked list because cur After changing the direction, the following linked list is invalid, so it needs to be saved
Next, the loop performs the following three operations
1)nex = cur->next, Preservation function
2)cur->next = pre The next pointer of the first node of the non inverted linked list points to the last node of the inverted linked list
3)pre = cur, cur = nex; Move the pointer backward to operate the first node of the next non inverted linked list
Cyclic conditions, of course cur != nullptr
At the end of the cycle, cur Of course nullptr,So return pre,That is, the inverted head node
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};*/
class Solution {
public:
ListNode* ReverseList(ListNode* pHead) {
ListNode* cur=pHead;
ListNode* next=nullptr;
ListNode* pre=nullptr;
while(cur){
next=cur->next;
cur->next=pre;
pre=cur;
cur=next;
}
return pre;
}
};
- Merge two sorted linked lists
describe
Enter two incremental linked lists. The length of a single linked list is n. merge the two linked lists and make the nodes in the new linked list still be sorted incrementally.
Data range: 0 ≤ n ≤ 1000, - 1000 ≤ node value ≤ 1000
Requirements: space complexity O(1), time complexity O(n)
If you enter {1,3,5}, {2,4,6}, the combined linked list is {1,2,3,4,5,6}, so the corresponding output is {1,2,3,4,5,6}
Iterative method:
Initialization: definition cur Point to the head node of the new linked list
Operation:
If l1 The node value pointed to is less than or equal to l2 Point the value of the node to l1 The node value pointed to is linked to cur of next Pointer, then l1 Point to the next node value
Otherwise, let l2 Point to the next node value
Cycle step 1,2,until l1 perhaps l2 by nullptr
take l1 perhaps l2 The rest is linked to cur Behind
skill
Generally, when creating a single linked list, you will set up a virtual head node, also known as sentry, because each node has a precursor node.
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};*/
class Solution {
public:
ListNode* Merge(ListNode* pHead1, ListNode* pHead2) {
ListNode* vhead = new ListNode(-1);
ListNode* cur = vhead;
while(pHead1 && pHead2){
if(pHead1->val<=pHead2->val){
cur->next=pHead1;
pHead1=pHead1->next;
}
else{
cur->next=pHead2;
pHead2=pHead2->next;
}
cur=cur->next;
}
cur->next=pHead1?pHead1:pHead2;
return vhead->next;
}
};
- The first common node of two linked lists
describe
Enter two acyclic one-way linked lists and find their first public node. If there is no public node, it returns null. (note that because the incoming data is a linked list, the prompt of error test data is displayed in other ways to ensure that the incoming data is correct)
Data range: 0 ≤ 1000
Requirements: space complexity O(1), time complexity O(n)
Enter Description:
The input is divided into three segments. The first segment is the non-public part of the first linked list, the second segment is the non-public part of the second linked list, and the third segment is the public part of the first linked list and the second linked list. The background will assemble the three parameters into two linked lists, and pass the corresponding header nodes of the two linked lists into the function FindFirstCommonNode. The user will get only pHead1 and pHead2 inputs.
Return value Description:
Return the first public node of the incoming pHead1 and pHead2, and the linked list with this node as the head node will be printed in the background.
Input: {1,2,3}, {4,5}, {6,7}
Output: {6,7}
Note: the first parameter {1,2,3} represents the non-public part of the first linked list, the second parameter {4,5} represents the non-public part of the second linked list, and the last {6,7} represents the public part of the two linked lists
These three parameters will finally be assembled into two acyclic single linked lists with public nodes in the background
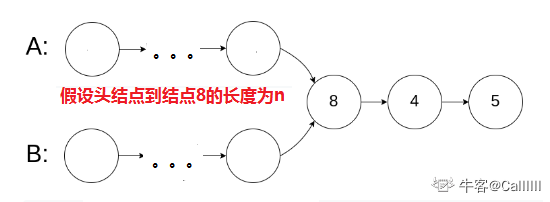
Double finger needling
Let's assume a linked list A Length and linked list of head node and node 8 B If the length of the head node is equal to that of node 8, double pointers can be used.
Initializing: pointers ta Point to linked list A Head node, pointer tb Point to linked list B Head node
If ta == tb, It indicates that the first public header node is found and can be returned directly.
Otherwise, ta != tb,be++ta,++tb
So now the question becomes, how to make the original length unequal become equal?
Hypothetical linked list A Count Reg a, Linked list B The length of the is b,here a != b
But, a+b == b+a
Therefore, you can make a+b As a linked list A New length, b+a As a linked list B New length of.
In this way, the length is consistent, and the above double pointer solution can be used.
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};*/
class Solution {
public:
ListNode* FindFirstCommonNode( ListNode* pHead1, ListNode* pHead2) {
ListNode* a=pHead1;
ListNode* b=pHead2;
while(a!=b){
a= a ? a->next:pHead2;
b= b ? b->next:pHead1;
}
return a;
}
};
- The entry node of a link in a linked list
describe
Give a linked list with a length of n. if it contains a ring, please find the entry node of the ring of the linked list. Otherwise, null will be returned.
Data range: 0 ≤ 10000, 1 < = node value < = 10000
Requirements: space complexity O(1), time complexity O(n)
For example, when you enter {1,2}, {3,4,5}
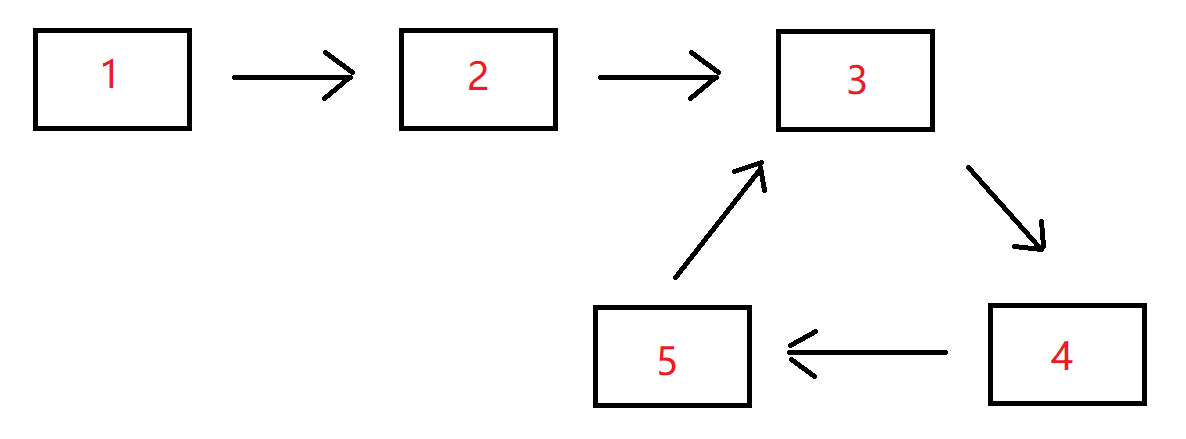
You can see that the node value of the entry node of the ring is 3, so the node with the node value of 3 is returned.
Abstract: given a single linked list, if there is a ring, return the entry node of the ring; otherwise, return nullptr
Method 1: Hashi method
Traverse each node of the single linked list
If the current node address does not appear in set If in, deposit set in
Otherwise, appear in set The current node is the entry node of the ring
After traversing the whole single linked list, if it does not appear in set In, there is no ring
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};
*/
class Solution {
public:
ListNode* EntryNodeOfLoop(ListNode* pHead) {
unordered_set<ListNode*> st;
while(pHead){
if(st.count(pHead)==0){
st.insert(pHead);
pHead=pHead->next;
}
else
return pHead;
}
return nullptr;
}
};
Knowledge points:
(1)unordered_ The set:: find() function is a built-in function in C++ STL, which is used to search for elements in the container. Call unordered_ Find () of set returns an iterator. This iterator points to the element that matches the parameter hash value. If there is no matching element, it will return the end iterator of this container
(2)unordered_ There can only be one matching element in the set container. If not, both iterators are the end iterators of the container. Calling the member function count() returns the number of occurrences of the parameter in the container. For unordered_set can only be 0 or 1. When you want to know the total number of elements in the container, you can call the member function size(). If there is no element in the container, the member function empty() returns true.
Method 2: speed pointer
By definition slow and fast Pointer, slow Every step, fast Take two steps. If there is a ring, you will meet at a node of the ring( slow == fast),According to the analysis and calculation, the distance from the meeting place to the entry node is the same as that between the head node and the entry node.
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};
*/
class Solution {
public:
ListNode* EntryNodeOfLoop(ListNode* pHead) {
if(!pHead)
return nullptr;
ListNode* fast=pHead;
ListNode* slow=pHead;
while(fast && fast->next){
fast=fast->next->next;
slow=slow->next;
if(fast==slow)
break;
}
if(!fast || !fast->next)
return nullptr;
fast=pHead;
while(fast!=slow){
fast=fast->next;
slow=slow->next;
}
return fast;
}
};
Detailed explanation:
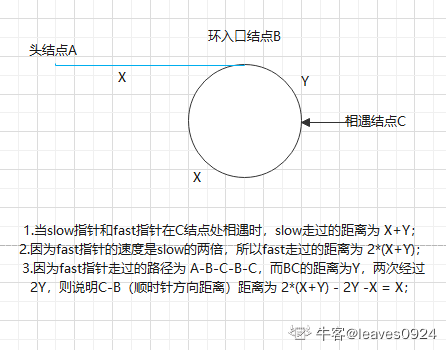
Then, when the fast and slow pointers arrive at the meeting node C at the same time, put the fast pointer fast back to the head node A, the position of the slow pointer slow remains unchanged, and the speed of the fast pointer is changed to be the same as that of the slow pointer slow. Then the fast pointer fast passes through the X distance from the head node A to the entrance node B of the ring, and the slow pointer slow also passes through the X distance from the fast and slow pointer meeting node C to the entrance node B of the ring, That is, the node when they meet again is the entry node of the ring.