recursion
Basic concepts
Recursion means that the method calls itself, and different variables are passed in each call. Recursion helps solve more complex problems than that, while making the code simpler
Call mechanism
Analysis of printing problems:

Recursive call rule:
- When the program executes a method, it will open up an independent space (stack)
- The data (local variables) of each space are independent; Reference data type variables are shared
package com.atguigu.recursion;
/**
* @ClassName RecursionDemo
* @Author Jeri
* @Date 2022-02-17 19:34
* @Description Recursive call mechanism
*/
public class RecursionDemo {
//Print problem
public static void test(int n){
if(n > 2){
test(n - 1);
}
System.out.println("n = " + n);
}
//Factorial problem
public static int factorial(int n){
if(n == 1){
return 1;
}else{
return n * factorial(n-1);
}
}
public static void main(String[] args) {
//Review the recursive call mechanism through printing problems
test(4);
int res = factorial(4);
System.out.println("res = " + res);
}
}
n = 2 n = 3 n = 4 res = 24
Usage scenario
- Various mathematical problems, such as: 8 queen problem, Hanoi Tower, factorial problem, maze problem, ball and basket problem (google programming competition)
- Recursion will also be used in various algorithms, such as fast sorting, merge sorting, binary search, divide and conquer algorithm, etc
- Problems to be solved with stack – > recursive code is relatively concise
Important rules
- When a method is executed, a new protected independent space (stack space) is created
- The local variables of the method are independent and will not affect each other
- If a reference type variable (such as an array) is used in a method, the data of that reference type will be shared
- Recursion must approach the condition of exiting recursion, otherwise it is infinite recursion. StackOverflowError appears and the turtle is dead:)
- When a method finishes executing or encounters a return, it will return. The result will be returned to the person who follows the call. At the same time, when the method finishes executing or returns, the method will be removed from the stack
Maze problem
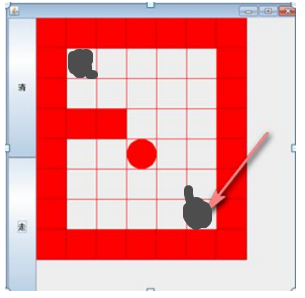
Problem Description: the red part is an obstacle. The small ball needs to move from the upper left corner to the lower right corner. Please give a path that can be moved
**Train of thought analysis: * * I can't write it myself. I don't know how to describe recursive backtracking
- The next location routing adopts the same strategy as the current location routing, so recursion is used
Code implementation:
package com.atguigu.recursion;
/**
* @ClassName Maze
* @Author Jeri
* @Date 2022-02-17 20:00
* @Description maze
*/
public class Maze {
public static int[][] maze;
public static int rows;
public static int lines;
/*
* @Description Set maze information
* @Date 2022/2/17 20:59
* @param rows Maze rows
* @param lines Number of labyrinth columns
**/
public static void setMaze(int rows,int lines){
//Create a two-dimensional array simulation maze
maze = new int[rows][lines];
//Maze digital state 1: obstacle 0: initial state 2: this road is open 3: this road is closed
//Maze set obstacles up and down two lines
for(int i = 0;i < 7;i++){
maze[0][i] = 1;
maze[7][i] = 1;
}
//Left and right columns
for(int i = 0;i < 8;i++){
maze[i][0] = 1;
maze[i][6] = 1;
}
//Special point
maze[3][1] = 1;
maze[3][2] = 1;
}
/*
* @Description Return maze information
* @Date 2022/2/17 20:59
**/
public static void getMaze(){
//Output map
System.out.println("Maze situation:");
for(int i = 0;i < rows;i++){
for(int j = 0;j < lines;j++){
System.out.printf(maze[i][j] + " ");
}
System.out.println();
}
}
/*
* @Description Pathfinding strategy
* @Date 2022/2/17 21:01
* @param i Abscissa
* @param j Ordinate
* maze[i][j] Represents the starting point of the maze
* If you can reach maze[6][5], it means that the path is found
* Agreement: Maze digital state 1: obstacle 0: initial state 2: this road is open 3: this road is closed
* When routing, you need to customize the routing strategy. Different routing strategies may get different paths
* @return maze[i][j]Is it accessible
**/
public static boolean setWay(int i,int j){
if(maze[6][5] == 2){
//The last node is through
return true;
}else{
//The ball starts to find its way from the node maze[i][j]
if(maze[i][j] == 0){
//0: initial state: the current node has not passed
//Set pathfinding strategy bottom right top left
//It is assumed that this point can go through
maze[i][j] = 2;
if(setWay(i + 1,j)){//lower
return true;
}else if(setWay(i,j + 1)){//right
return true;
}else if(setWay(i - 1 ,j)){//upper
return true;
}else if(setWay(i,j - 1)){//Left
return true;
}else{
//This point is a dead end
maze[i][j] = 3;
return false;
}
}else{
// maze[i][j] != 0, 1, 2, 3 can't pass this point
return false;
}
}
}
public static void main(String[] args) {
//View the map
rows = 8;
lines = 7;
setMaze(rows,lines);
getMaze();
//Using recursive pathfinding
setWay(1,1);
//Get maze information
//Connecting all points with the number 2 is the path
System.out.println();
System.out.println("Connecting all points with the number 2 is the path");
getMaze();
}
}
Maze situation: 1 1 1 1 1 1 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 1 1 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 Connecting all points with the number 2 is the path Maze situation: 1 1 1 1 1 1 1 1 2 0 0 0 0 1 1 2 2 2 0 0 1 1 1 1 2 0 0 1 1 0 0 2 0 0 1 1 0 0 2 0 0 1 1 0 0 2 2 2 1 1 1 1 1 1 1 1
Eight queens
**Problem Description: * * eight queens problem is an ancient and famous problem and a typical case of backtracking algorithm. The question was put forward by international chess player Max Bethel in 1848: in August × Eight queens are placed on the 8-grid chess so that they can't attack each other, that is, any two Queens can't be in the same row, column or slash. Ask how many kinds of pendulum methods there are (92).

Train of thought analysis:
- The first queen puts the first row and the first column first
- The second queen is placed in the first column of the second row, and then judge whether it is OK. If it is not OK, continue to put it in the second column and the third column, and replace all columns in turn
Finish it and find a suitable one - Continue the third queen, or the first and second columns... Until the eighth queen can also be placed in a non conflict position, it can be regarded as finding the right one
solution - When a correct solution is obtained, when the stack goes back to the previous stack, it will start backtracking, that is, the first queen will put all the correct solutions in the first column,
All get - Then go back and continue to put the first queen in the second column, and then continue to cycle through steps 1, 2, 3 and 4
**Note: * * theoretically, a two-dimensional array should be created to represent the chessboard, but in fact, the problem can be solved by using a one-dimensional array through algorithm arr[8] =
{0 , 4, 7, 5, 2, 6, 1, 3}
- arr[i] subscript i indicates the i-th row, i.e. the i-th queen, (Note: queen number is from 0-7)
- arr[i] = value, value means that the ith queen is placed in the value column (Note: the column where the queen is placed is from 0 to 7)
Note: in fact, violent solution is adopted, which is similar to 8-fold for loop. Using recursive algorithm makes the code concise and abstract. Recursive backtracking is equivalent to recording the checkpoint of the current layer of for loop. debug more
package com.atguigu.recursion;
/**
* @ClassName Queen8
* @Author Jeri
* @Date 2022-02-17 22:15
* @Description Eight queens problem
*/
public class Queen8 {
//max indicates the number of queens
public static int max;
//arr indicates where the queen is stored
public static int[] arr;
//count indicates the total number of solutions
public static int count = 0;
private void check(int n){
if(n == max){
print();
return;
}
//Judge whether the queen puts the conflict in turn
for(int i = 0;i < max;i++){
//Put the current queen in the first column first
arr[n] = i;
//Judge whether there is conflict between the nth queen and column i
if(!isConflict(n)){
//Place the next queen without conflict
check(n+1);
}
//Conflict for loop continues to execute arr[n] = i
//Move current position back
}
}
/*
* @Description Detect whether the nth queen conflicts with the first n-1 queen
* @Date 2022/2/17 22:46
* @param n The n th queen
* @return [n] false No conflict
*/
private boolean isConflict(int n){
for(int i = 0;i < n;i++){
//Queen conflict principle: any two queens cannot be in the same row, column or slash
//1. Any two queens after one-dimensional array representation in the same row cannot be in the same row
//2. The same column arr[i] == arr[n]
//3. Same slash ABS (ordinate / abscissa) = 1
// Math.abs(n-i) == Math.abs(arr[n] - arr[i])
if(arr[i] == arr[n] || Math.abs(n-i) == Math.abs(arr[n] - arr[i])){
return true;
}
}
return false;
}
/*
* @Description Output Queen's placement position
* @Date 2022/2/17 22:16
**/
private void print(){
count++;
for(int i = 0; i < arr.length;i++){
System.out.printf(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
//max indicates the number of queens
max = 8;
//arr indicates where the queen is stored
arr = new int[max];
Queen8 queen8 = new Queen8();
queen8.check(0);
System.out.printf("Total%d A solution\n",count);
}
}
0 4 7 5 2 6 1 3 0 5 7 2 6 3 1 4 0 6 3 5 7 1 4 2 0 6 4 7 1 3 5 2 1 3 5 7 2 0 6 4 1 4 6 0 2 7 5 3 1 4 6 3 0 7 5 2 1 5 0 6 3 7 2 4 1 5 7 2 0 3 6 4 1 6 2 5 7 4 0 3 1 6 4 7 0 3 5 2 1 7 5 0 2 4 6 3 2 0 6 4 7 1 3 5 2 4 1 7 0 6 3 5 2 4 1 7 5 3 6 0 2 4 6 0 3 1 7 5 2 4 7 3 0 6 1 5 2 5 1 4 7 0 6 3 2 5 1 6 0 3 7 4 2 5 1 6 4 0 7 3 2 5 3 0 7 4 6 1 2 5 3 1 7 4 6 0 2 5 7 0 3 6 4 1 2 5 7 0 4 6 1 3 2 5 7 1 3 0 6 4 2 6 1 7 4 0 3 5 2 6 1 7 5 3 0 4 2 7 3 6 0 5 1 4 3 0 4 7 1 6 2 5 3 0 4 7 5 2 6 1 3 1 4 7 5 0 2 6 3 1 6 2 5 7 0 4 3 1 6 2 5 7 4 0 3 1 6 4 0 7 5 2 3 1 7 4 6 0 2 5 3 1 7 5 0 2 4 6 3 5 0 4 1 7 2 6 3 5 7 1 6 0 2 4 3 5 7 2 0 6 4 1 3 6 0 7 4 1 5 2 3 6 2 7 1 4 0 5 3 6 4 1 5 0 2 7 3 6 4 2 0 5 7 1 3 7 0 2 5 1 6 4 3 7 0 4 6 1 5 2 3 7 4 2 0 6 1 5 4 0 3 5 7 1 6 2 4 0 7 3 1 6 2 5 4 0 7 5 2 6 1 3 4 1 3 5 7 2 0 6 4 1 3 6 2 7 5 0 4 1 5 0 6 3 7 2 4 1 7 0 3 6 2 5 4 2 0 5 7 1 3 6 4 2 0 6 1 7 5 3 4 2 7 3 6 0 5 1 4 6 0 2 7 5 3 1 4 6 0 3 1 7 5 2 4 6 1 3 7 0 2 5 4 6 1 5 2 0 3 7 4 6 1 5 2 0 7 3 4 6 3 0 2 7 5 1 4 7 3 0 2 5 1 6 4 7 3 0 6 1 5 2 5 0 4 1 7 2 6 3 5 1 6 0 2 4 7 3 5 1 6 0 3 7 4 2 5 2 0 6 4 7 1 3 5 2 0 7 3 1 6 4 5 2 0 7 4 1 3 6 5 2 4 6 0 3 1 7 5 2 4 7 0 3 1 6 5 2 6 1 3 7 0 4 5 2 6 1 7 4 0 3 5 2 6 3 0 7 1 4 5 3 0 4 7 1 6 2 5 3 1 7 4 6 0 2 5 3 6 0 2 4 1 7 5 3 6 0 7 1 4 2 5 7 1 3 0 6 4 2 6 0 2 7 5 3 1 4 6 1 3 0 7 4 2 5 6 1 5 2 0 3 7 4 6 2 0 5 7 4 1 3 6 2 7 1 4 0 5 3 6 3 1 4 7 0 2 5 6 3 1 7 5 0 2 4 6 4 2 0 5 7 1 3 7 1 3 0 6 4 2 5 7 1 4 2 0 6 3 5 7 2 0 5 1 4 6 3 7 3 0 2 5 1 6 4 There are 92 solutions in total