Reference Textbook: Proficiency in C++ (9th Edition)

Recursive function: a self-calling function
Functions can also call themselves

Example:

#include<iostream>
void message(int times)
{
if (times > 0)
std::cout << "You are pretty beautiful!!!\n" <<std:: endl;
message(times - 1);//control power
}
int main()
{
 
message(3);
return 0;
}

Functions are called four times, so the depth of recursion is: 4;

Direct Recursion and Indirect Recursion: One calls its own function directly, the other calls indirectly. A calls B,B calls C,C calls A.

Example: Recursive factorial calculation: Receiving an integer parameter and calculating its factorial
Factorial (n)=n*factorial(n-1); if n > 1;
=1;n=1

#include<iostream>
//#include<string>
int factorial(int arg)
{
	if (arg == 1)
		return 1;
	else
		return arg * factorial(arg - 1);

}
int main()
{
	int number;
	std::cout << "Enter an number and I will dispaly it's factorial:\n";
	std::cin >> number;
	std::cout << "It is equal to " << factorial(number) << std::endl;
	return 0;
}

Recursive calculation of maximum common divisions: greastest common divisior,GCD
Rolling phase division
Rotary phase division: Rotary phase division is a method of finding the greatest common divisor of two natural numbers, also known as Euclidean algorithm.
Come from https://baike.baidu.com/item/maximum common divisor

gcd(x,y)=y; if y is divided by x, there is no remainder
= gcd(y,x/y remainder)

#include<iostream>
//#include<string>
int gcd(int x, int y)
{
	if ( x% y== 0)
		return y;
	else
		return gcd(y, x % y);
}
int main()
{
	int x, y;
	std::cout << "Enter two integers:\n";
	std::cin >> x >> y;
	std::cout << "The two integers' greatest common divisor is " << gcd(x, y) << std::endl;

	return 0;
}

#include<iostream>
//#include<string>

int fib(int n)
{
	if (n <= 0)
		return 0;
	else if (n == 1)
		return 1;
	else
		return fib(n - 1) + fib(n - 2);
}
int main()
{
	std::cout << "The first Fibonacci numbers are: \n";
	for (int i = 0; i < 10; i++)
	{
		std::cout << fib(i) << std::endl;
	}
	return 0;
}

Example: Recursive Binary Search Function: Binary Search can be defined as a Recursive Function

int binarySearch(const int array[], int first ,int last ,int value)
Main parts:

int middle;
    if(first>last)
  return -1;
     if(array[middle]<value)
 return binarySearch( const int array[], int middle+1 ,int last ,int value)
    if(array[middle]>value)
 return binarySearch( const int array[], int first ,int middle-1 ,int value)

Array is an array to search for. The first and last parameters retain the search scope. value finds the target.

#include<iostream>
int binarySearch(const int list[], int first, int last, int value)
{
	int middle=(first+last)/2;
	bool found = false;
	if (first > last)
		return -1;
	if (list[middle] == value)
		return middle;
	if (list[middle] > value)
		return binarySearch(list, first, middle - 1, value);
	else
		return binarySearch(list, middle + 1, last, value);
}
const int SIZE = 20;
int main()
{
	int array[SIZE] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,89,99,100 };
	int number, results;
	std::cout << "Enter an integer to search in the list\n";
	std::cin >> number;
	results = binarySearch(array, 0,SIZE-1, number);
	if (results == -1)
		std::cout << "That's number isn't exist in the array\n";
	else
	std::cout << "the number " << number << " you had search, is on the position" << results + 1 << std::endl;
	return 0;
}

Example: Programming and Programming: Quick Sorting Algorithms
Use recursion to sort lists effectively:
A recursive function, usually with three parameters, that defines a part of the array to be sorted.
An array arr containing a list of items
Two subscripts start and end
Pseudo-code:

void Quick Sorting( int arr[],int start, int end)
{
If(start<end)
{
Int p=partition(arr,start,end);//Partitioning the array and obtaining the pivot
//Sort less than base elements
//Quick sort (arr,start,p-1);
//Sort larger than base elements
//Quick sort (arr,p+1,end)
}
}

Difficulty: Understand the split array arr[start... end] process,
The partitioning algorithm chooses arr[start] as the base element, and constructs two sub-elements on the left side and right side of the base element in stages.

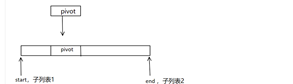
Repeat partitioning, sorting: row x just at the end of sublist 2, assuming x < pivot, to be added to sublist 1 of the start group
Method: Add it to the end of sublist 1 and place it on the left of pivot.
Strategy: Store x in a temporary location, move the elements of sublist 2 to the right, and then put x in the position vacated by pivot, which is inefficient.
The first exchange places y (>= pivot) at the end of sublist 2, while the second exchange places x adjacent to pivot, and the second exchange places x on the left of pivot.
Repeat until the entire list partition
partition function code for executing partitions (incomplete)

int partition(int arr[],int start, int end)
{
 int pivotValue=arr[start];
 int  pivotposition=start;
 
//The elements from start to end in the rearrangement region, except the reference elements
 for(int pos=start+1;pos<=end;pos++)
{
If(arr[pos]<pivotValue)
{
Swap(arr[pivotPosition+1],arr[pos];//Change of position
Swap(arr[pivotPosition],arr[pivotPosition+1];
pivotPosition++;
}
}
 return pivotPosition;
} 

Code:

#include<iostream>
#Include < algorithm >//swap function
using namespace std;
int quicksort(int[], int, int);//Quick sort
int  partition(int[], int, int);//partition

int main()
{
	const int SIZE = 10;
	int array[SIZE] = { 17,45,6,89,65,33,83,24,45,76 };
	for (int k = 0; k < SIZE; k++)
	{
		cout << array[k] << " " ;
	}
	cout << endl;
	quicksort(array, 0, SIZE);
	for (int k = 0; k < SIZE; k++)
	{
		cout << array[k] << " " ;
	}
	cout << endl;
	return 0;
}
int partition(int arry[], int start, int end)
{
	int pivotValue = arry[start];
	int pivotPosition = start;

	//The elements from start to end in the rearrangement region, except the reference elements
	for (int pos = start + 1; pos <= end; pos++)
	{
		if(arry[pos] < pivotValue)
		{
			swap(arry[pivotPosition + 1], arry[pos]);//Change of position
			swap(arry[pivotPosition], arry[pivotPosition + 1]);
			pivotPosition++;
		}
	}
	return pivotPosition;


}
int quicksort(int arry[], int start, int end)
{
	if (start < end)
	{
		int p = partition(arry, start, end);//Give the array partition and get the reference point

		quicksort(arry, start, p - 1);//Obtain intervals smaller than base elements

		quicksort(arry, p + 1, end);//Obtain intervals larger than base elements

	}
	return 0;
}

ps: It seems that I have a little bug running out with vs, but dev has no problem running out.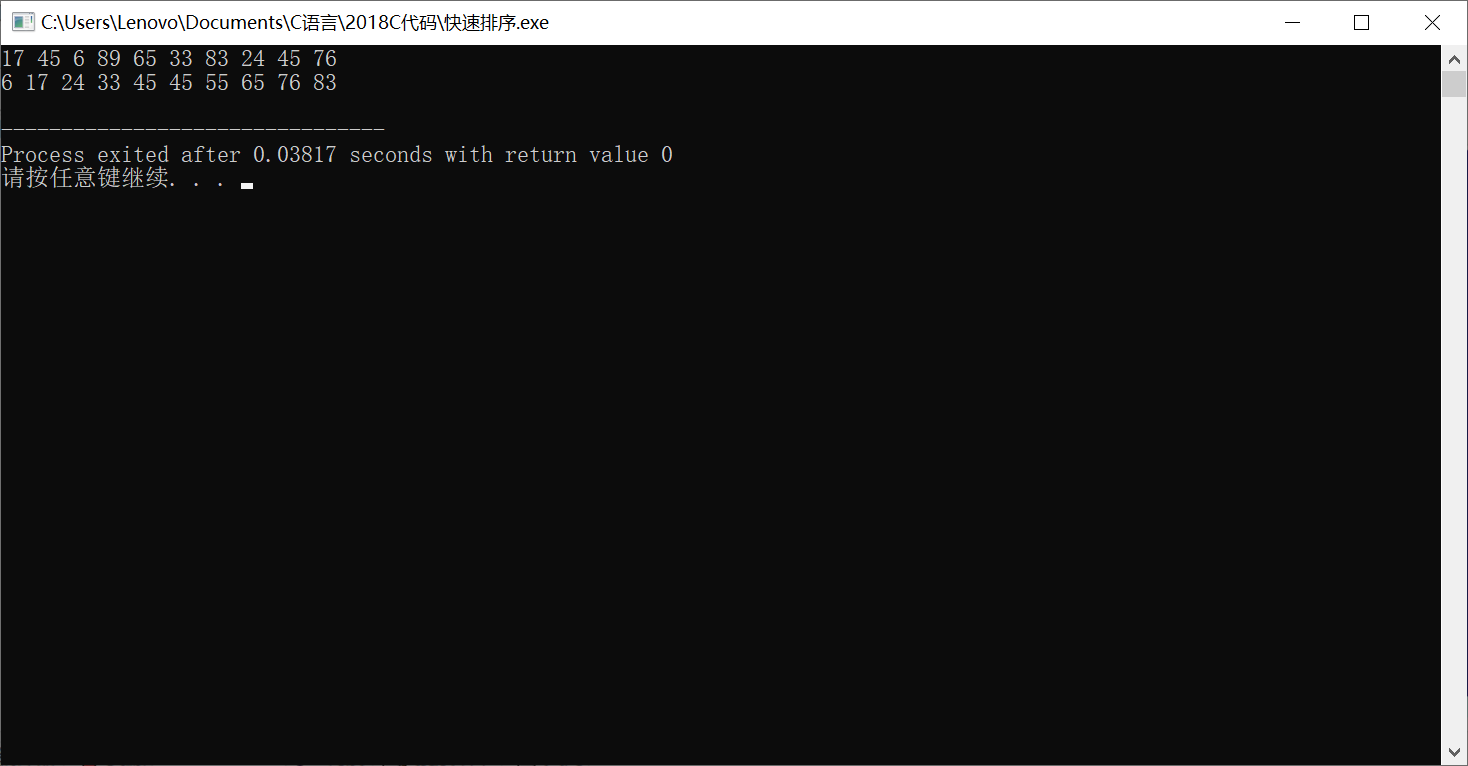

Example: Tower of Hanoi
cheer up!