Binary tree

The so-called traversal refers to one and only one visit to each node in the tree along a search route. The operation of the access node depends on the specific application problem (for example, print the node content and add 1 to the node content). Traversal is one of the most important operations on a binary tree. It is a binary tree forward
The basis of other operations.

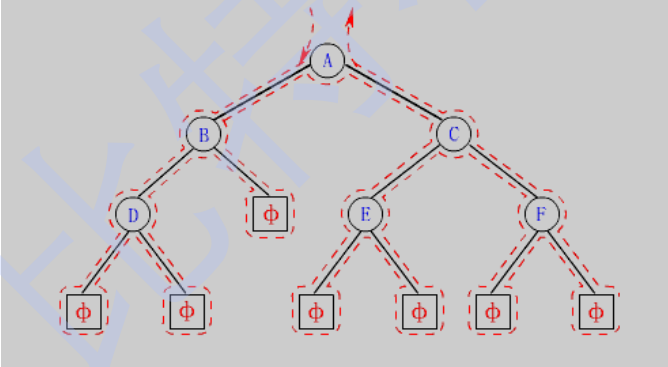
When traversing a binary tree, if there is no agreement, everyone traverses it in their own way, and the results are chaotic. If there is an agreement according to some rules, everyone must have the same traversal result for the same tree. If N represents the root node, L represents the left subtree of the root node, and R represents the right subtree of the root node, there are the following traversal methods according to the order of traversing the root node:

1. NLR: Preorder traversal(Preorder Traversal Also known as preorder traversal)-Access root node--->Left subtree of root--->Right subtree of root.
2. LNR: Middle order traversal(Inorder Traversal)-Left subtree of root--->Root node--->Right subtree of root.
3. LRN: Postorder traversal(Postorder Traversal)-Left subtree of root--->Right subtree of root--->Root node.

Since the accessed node must be the root of a subtree, N(Node), L(Left subtree) and R(Right subtree) can be interpreted as the root, the left subtree of the root and the right subtree of the root. NLR, LNR and LRN are also called first root traversal, middle root traversal and second root traversal respectively.

Recursive traversal

Recursive traversal code is relatively simple

Preorder traversal, inorder traversal, postorder traversal

/**
     *Recursive traversal
     */
    // Preorder traversal
    void preOrderTraversal(Node root){
        if (root == null) return;
        System.out.print(root.val+" ");
        preOrderTraversal(root.left);
        preOrderTraversal(root.right);

    }
    // Middle order traversal
    void inOrderTraversal(Node root){
        if (root == null) return;
        inOrderTraversal(root.left);
        System.out.print(root.val+" ");
        inOrderTraversal(root.right);
    }
    // Postorder traversal
    void postOrderTraversal(Node root){
        if (root == null) return;
        postOrderTraversal(root.left);
        postOrderTraversal(root.right);
        System.out.print(root.val+" ");
    }

Iterative traversal

Iterative traversal uses the stack to simulate the traversal process, and makes one and only one access to each node in the tree in turn. The operation of the access node depends on the specific application problem (for example, printing the node content)

Preorder traversal, inorder traversal, postorder traversal

/**
     * Non recursive traversal
     */
    // Preorder traversal
    void preOrderTraversalNor(Node root) {
        if (root == null) {
            return;
        }
        Stack<Node> stack = new Stack<>();
        Node cur = root;
        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                stack.push(cur);
                System.out.print(cur.val+" ");
                cur = cur.left;
            }
            Node top = stack.pop();
            cur = top.right;
        }
    }
    // Middle order traversal
    void inOrderTraversalNor(Node root) {
        if (root == null) {
            return;
        }
        Stack<Node> stack = new Stack<>();
        Node cur = root;
        while (cur !=null || !stack.isEmpty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            Node top = stack.pop();//Take stack top
            System.out.print(top.val+" ");
            cur = top.right;
        }
    }

    // Postorder traversal
    void postOrderTraversalNor(Node root) {
        if (root == null) return;
        Stack<Node> stack = new Stack<>();
        Node cur = root;
        Node prev = null;
        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            cur = stack.peek();//
            if (cur.right == null || cur.right == prev) {//If cur Right is equal to the printed value. Go in and out of the loop pop() and print the top element of the stack
                stack.pop();
                System.out.print(cur.val+" ");
                prev = cur;//Record the value printed by cur
                cur = null;//cur is set to null to avoid entering the internal while loop and prevent the printed elements from being put on the stack again

            } else {
                cur = cur.right;
            }
        }
    }

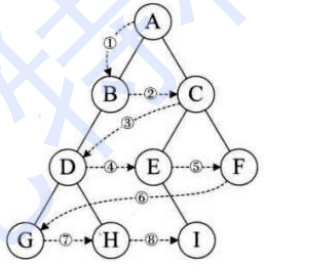
Sequence traversal (using queues)

Set the number of layers where the root node of the binary tree is located as 1. Sequence traversal starts from the root node of the binary tree, first visit the root node of the first layer, and then
The process of accessing the nodes of the tree layer by layer from left to right, followed by the nodes of the third layer, and so on
Sequence traversal.

// level traversal 
    void levelOrderTraversal(Node root){
        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            Node cur = queue.poll();
            //Access element
            System.out.print(cur.val+" ");
            //Queue left and right subtrees
            if (cur.left != null) {
                queue.offer(cur.left);
            }
            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }
    }

balanced binary tree

Judge whether a binary tree is a balanced binary tree

The absolute value of the height difference between the left and right subtrees of each node shall not exceed 1

 public boolean isBalanced(Node root) {
        if (root == null) return true;
        if (root.left == null && root.right == null) return true;
        //Check whether the subtree corresponding to the current node is balanced
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);
        if (leftHeight-rightHeight > 1 || leftHeight-rightHeight < -1) {
            return false;
        }
        return isBalanced(root.left) && isBalanced(root.right);
    }

Complete binary tree

Judge whether a binary tree is a complete binary tree

There is no gap in the middle

 boolean isCompleteTree(Node root){
        if (root == null) return true;
        //1. Queue
        Queue<Node> queue = new LinkedList<>();
        //2. Throw elements into the queue and get out of the queue (= = null)
        queue.offer(root);
        while (!queue.isEmpty()) {
             Node cur = queue.poll();
             if (cur != null) {
                 queue.offer(cur.left);
                 queue.offer(cur.right);
             } else {
                 break;
             }
        }
        //When the code comes here, it shows that the while loop above is a break, and the cur node of poll must be empty
        //3. Continue to judge the queue. If it is all null, it is true, otherwise it is false (because if it is a complete binary tree, the pop-up element of a single order is null, and the following must be empty)
        while (!queue.isEmpty()) {
            Node cur = queue.poll();
            if (cur != null) {
                return false;
            }
        }
        return  true;
    }