Red black tree

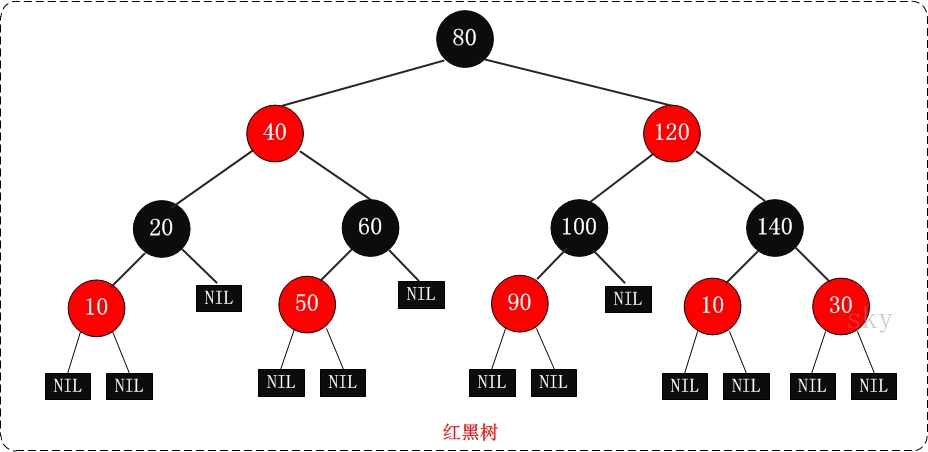
Red black tree is a binary lookup tree with color attribute for each node, either red or black. In addition to the mandatory General requirements for binary search trees, we have added the following additional requirements for any effective red black tree:

Nature 1 Nodes are red or black.

Nature 2 The root node is black.

Nature 3 Each leaf node (NIL node, empty node) is black.

Nature 4 The two children of each red node are black. (there cannot be two consecutive red nodes on all paths from each leaf to the root)

Nature 5 All paths from any node to each of its leaves contain the same number of black nodes.

These constraints enforce the key property of red black trees: the longest possible path from root to leaf is no more than twice the length of the shortest possible path. The result is that the tree is roughly balanced. Because the worst-case time of operations such as inserting, deleting and finding a value is required to be proportional to the height of the tree, this theoretical upper limit on the height allows the red black tree to be efficient in the worst-case, which is different from the ordinary binary search tree.

To know why these features ensure this result, it is sufficient to note that property 4 causes the path not to have two adjacent red nodes. The shortest possible paths are black nodes, and the longest possible paths have alternating red and black nodes. Because according to property 5, all the longest paths have the same number of black nodes, this indicates that no path can be twice as long as any other path.

In the representation of many tree data structures, a node may have only one child node, while the leaf node does not contain data. It is possible to represent the red black tree with this example, but it will change some properties and complicate the algorithm. For this purpose, we use "nil leaf" or "null leaf" in this article. As shown in the above figure, it does not contain data, but only serves as an indication that the tree ends here. These nodes are often omitted in the drawing, which makes these trees seem to contradict the above principles, but in fact they are not. The related conclusion is that all nodes have two child nodes, although one or two of them may be empty leaves.

code implementation

#include "rbtree.h"

#define ISBLACK(node) (node==NULL || node->color==BLACK)


/*
typedef int ETYPE;

enum COL{RED=0,BLACK=1};

typedef struct RBNode
{
	ETYPE elem;
	char color;
	struct RBNode *lchild;
	struct RBNode *rchild;
	struct RBNode *parent;
}RBNode;
typedef struct RBNode * RBTree;
*/ 
static void left(RBTree *proot,RBTree node)
{
	RBTree right=node->rchild;
	right->parent=node->parent;
	if(node->parent!=NULL)
	{
		if(node==node->parent->lchild)
		{
			node->parent->lchild=right;
		}
		else
		{
			node->parent->rchild=right;
		}
	}
	else
	{
		*proot=right; 
	}
	node->rchild=right->lchild;
	if(right->lchild!=NULL)
	{
		right->lchild->parent=node;
	}
	right->lchild=node;
	node->parent=right;
}

static void right(RBTree *proot,RBTree node)
{
	RBTree left=node->lchild;
	left->parent=node->parent;
	if(node->parent!=NULL)
	{
		if(node==node->parent->lchild)
		{
			node->parent->lchild=left;
		}
		else
		{
			node->parent->rchild=left;
		}
	}
	else
	{
		*proot=left; 
	}
	node->lchild=left->rchild;
	if(left->rchild!=NULL)
	{
		left->rchild->parent=node;
	}
	left->rchild=node;
	node->parent=left;
}

static void rb_insert_repair(RBTree *proot,RBTree node)
{
	RBTree parent=node->parent;
	while(node->color==RED && node->parent!=NULL && parent->color==RED)
	{
		RBTree gp=parent->parent;
		RBTree uncle=gp->lchild==parent?gp->rchild:gp->lchild;
		if(uncle!=NULL && uncle->color==RED)
		{
			parent->color=BLACK;
			uncle->color=BLACK;
			gp->color=RED;
			node=gp;
			parent=node->parent;
		}
		else
		{
			if(gp->lchild==parent)
			{
				if(parent->rchild==node)//lr becomes ll 
				{
					left(proot,parent);
					node=parent;
					parent=node->parent;
				}
				right(proot,gp);//ll
				gp->color=RED;
				parent->color=BLACK;
			} 
			else
			{
				if(parent->rchild==node)
				{
					right(proot,parent);//rl becomes rr 
					node=parent;
					parent=node->parent;
				}
				left(proot,gp);//rr
				gp->color=RED;
				parent->color=BLACK;
			}
			break;
		}
	}
	
	(*proot)->color=BLACK;		
}

static RBTree rb_create_node(int elem,RBTree parent)
{
	RBTree node=malloc(sizeof(RBNode));
	if(node==NULL)
	{
		return NULL;
	}
	node->color=RED;
	node->elem=elem;
	node->lchild=NULL;
	node->rchild=NULL;
	node->parent=parent;
	return node;
}

int rb_insert(RBTree *proot,ETYPE elem)
{	
	RBTree parent=NULL;
	RBTree *ptree=proot;
	while((*ptree)!=NULL)
	{
		parent=*ptree;
		if((*ptree)->elem>elem)
		{
			ptree=&(*ptree)->lchild;	
		}
		else if((*ptree)->elem<elem)
		{
			ptree=&(*ptree)->rchild;
		}
		else
		{
			return -1;	
		}	
	}
	(*ptree)->elem=elem;
	(*ptree)->lchild=NULL;
	(*ptree)->rchild=NULL;
	(*ptree)->parent=parent;
	rb_insert_repair(proot,*ptree);
	return 0;	
}
static void rb_delete_repair(RBTree *proot,RBTree parent,RBTree node)
{
	while(node==NULL && (node==NULL || node->color==BLACK))
	{
		RBTree brother=parent->lchild==node?parent->rchild:parent->lchild;
		if(node==parent->lchild)
		{
			if(brother->color==RED)
			{
				brother->color=BLACK;
				parent->color=RED;
				left(proot,parent);
				brother=parent->rchild; 
			}
			if(ISBLACK(brother) && ISBLACK(brother->lchild) && ISBLACK(brother->rchild))
			{
				if(parent->color==RED)
				{
					parent->color=BLACK;
					brother->color=RED;
					break;
				}
				else
				{
					brother->color=RED;
					node=parent;
					parent=node->parent;
					continue; 
				}
			}
			if(ISBLACK(brother->rchild))
			{
				brother->color=RED;
				brother->lchild->color=BLACK;
				right(proot,brother);
				brother=brother->parent; 
			}
			brother->color=parent->color;
			parent->color=BLACK;
			brother->rchild->color=BLACK;
			left(proot,parent);
			break; 
		}
		else
		{
			if(brother->color==RED)
			{
				parent->color=RED;
				brother->color=BLACK;
				right(proot,parent); 
				brother=parent->lchild;
			}	
			if(ISBLACK(brother) && ISBLACK(brother->lchild) && ISBLACK(brother->rchild))
			{
				if(parent->color==RED)
				{
					parent->color=BLACK;
					brother->color=RED;
					break;
				}
				else
				{
					brother->color=RED;
					node=parent;
					parent=node->parent;
					continue; 
				}
			}
			if(ISBLACK(brother->lchild))
			{
				brother->color=RED;
				brother->rchild->color=BLACK;
				left(proot,brother);
				brother=brother->parent; 
			}
			brother->color=parent->color;
			parent->color=BLACK;
			brother->lchild->color=BLACK;
			right(proot,parent);
			break; 
		} 
	}
}

static void rb_delete_node(RBTree *proot,RBTree *pnode)
{
	RBTree node=*pnode;
	if(node->lchild==NULL && node->rchild==NULL)
	{
		if(node->color==RED)
		{
			*pnode=NULL;
			free(node);
		}
		else
		{
			RBTree parent=node->parent;
			*pnode=NULL;
			free(node);
			rb_delete_repair(proot,parent,NULL);
		}
	} 
	else if(node->lchild!=NULL && node->rchild!=NULL)
	{
		for(pnode=&(*pnode)->lchild;(*pnode)->rchild!=NULL;pnode=&(*pnode)->rchild);
		node->elem=(*pnode)->elem;
		rb_delete_node(proot,pnode);
	}
	else
	{
		*pnode=node->lchild!=NULL?node->lchild:node->rchild;
		(*pnode)->color=BLACK;
		(*pnode)->parent=node->parent; 
		free(node);
	}
}

int rb_delete(RBTree *proot,ETYPE elem)
{
	RBTree *ptree=proot;
	while(*ptree!=NULL)
	{
		if(elem==(*ptree)->elem)
		{
			rb_delete_node(proot,ptree);
			return 0;
		}
		else if(elem<(*ptree)->elem)
		{
			ptree=&(*ptree)->lchild;
		}
		else
		{
			ptree=&(*ptree)->rchild;
		}
	}
	return -1;	
}