Continued Red black tree, insertion and deletion, better understanding , in this article, I won't introduce the understanding part too much, because what I said in the last article is almost the same. Next, I will implement the red black tree based on C + +. Similarly, you are welcome to ask questions and point out errors in the comment area!
First, we need to build the node class of the red black tree. In this class, there should be key value, value value, node color, node class pointers to the left and right child nodes, and finally add node class pointers to the parent node. Here, I set the key value as int type and the value value as string type. The color of the node is represented by bool type, that is, true indicates red and false indicates black.
class Node_RB {
public:
int m_key;
string m_value;
bool m_color;
Node_RB* m_left;
Node_RB* m_right;
Node_RB* m_parent;
Node_RB(int k, string v,bool c,Node_RB* l,Node_RB* r,Node_RB* p) {
m_key = k;
m_value = v;
m_color = c;
m_left = l;
m_right = r;
m_parent = p;
}
};Next, we will start to write our red black tree class. The member variables of this class are similar to binary trees. There are also root nodes and M representing the number of nodes_ n. At the same time, we know that we often use left-handed and right-handed functions in insertion and deletion, so we also write these two functions in advance. I also refer to the notes Complete tutorial of Ali P7 big man tearing red and black trees by hand , it has been written in great detail, so I won't repeat it too much.
class RB_tree {
public:
Node_RB* root;
int m_n;
RB_tree() {
m_n = 0;
root = NULL;
}
/* Left rotation, with p as the fulcrum, note that remember to consider the parent node of p and how to connect the parent node of p
p pr
/\ /\
pl pr => p rr
/\ /\
rl rr pl rl
*/
void left_rotate(Node_RB* p) {
// temp = pr; Right node of P = rl; The parent node of rl is set to p; Parent node of PR = parent node of p; The parent node of P is connected to PR; Parent node of P = PR; Left node of PR = p;
Node_RB* temp = p->m_right; //It's pr
p->m_right = temp->m_left;
if (p->m_right != NULL) {
//If rl is not empty, set the parent node of rl to p
p->m_right->m_parent = p;
}
temp->m_parent = p->m_parent; //Is p the left or right node of its parent node, or is it root
if (p->m_parent == NULL) {
//p is the root node
root = temp;
}
else if (p->m_parent->m_left == p) {
//p is the left node
p->m_parent->m_left = temp;
}
else if (p->m_parent->m_right == p) {
//p is the right node
p->m_parent->m_right = temp;
}
p->m_parent = temp;
temp->m_left = p;
}
/* Dextral with p as fulcrum
p pl
/\ /\
pl pr => rl p
/\ /\
rl rr rr pr
*/
void right_rotate(Node_RB* p) {
Node_RB* temp = p->m_left; //pl
p->m_left = temp->m_right;
if (p->m_left != NULL) {
p->m_left->m_parent = p;
}
temp->m_parent = p->m_parent;
if (p->m_parent == NULL) {
root = temp;
}
else if (p->m_parent->m_left == p) {
p->m_parent->m_left = temp;
}
else if (p->m_parent->m_right == p) {
p->m_parent->m_right = temp;
}
temp->m_right = p;
p->m_parent = temp;
}
}Let's start with one of our two most important parts: insertion
Review what I summarized in the previous article:
1. Empty tree: as the root node, it becomes black false
2. There is an existing key, just change the value
3. The parent node is a black node: you can add it directly without changing it
The first three cases have been handled, and the adjust function handles the following cases
4. The parent node is red: (then the grandpa node must be black, and the uncle node is either not or red. If the uncle node is black, it will be unbalanced and the depth of the uncle will be large)
1. The node does not exist
The inserted node is on the same side as the parent node
On the left, rotate right with Grandpa node as the fulcrum, then change the parent node to black and grandpa node to red
They are all on the right, with Grandpa's node as the fulcrum, and the color change is the same as above
The inserted node and the parent node are not on the same side
The parent node is on the left, and the parent node is used as the fulcrum to rotate left, which is converted to the case on the same side above. Here, the color changes are self and self Grandpa, please note that after the rotation, who is the parent node and who is the grandpa node
The parent node is on the right side and rotates right with the parent node as the fulcrum, which is converted to the case on the same side above
2. The uncle node is red. In this case, it may be necessary to iterate from bottom to top, because this makes the grandpa node red, and the grandpa's parent node may also be red
Just change color, Grandpa node turns red, and parent node and uncle node turn black
void put(int k, string v) {
Node_RB* n = root;
Node_RB* np = root;
if (n == NULL) {
//Insert the first node into the empty tree
root = new Node_RB(k, v, false, NULL, NULL, NULL);
m_n = 1;
return;
}
//Find out where this node is first
while (n != NULL) {
np = n;//Record parent node
if (n->m_key == k) {
//If there is an existing key, just change the value directly
n->m_value = v;
return;
}
else if (k < n->m_key) {
n = n->m_left;
}
else {
n = n->m_right;
}
}
//First, let the parent node of the insertion node point to np
Node_RB* n_new = new Node_RB(k, v, true, NULL, NULL, np);
//Judge whether this node is on the left or right of np
if (k < np->m_key) {
np->m_left = n_new;
}
else {
np->m_right = n_new;
}
//Judge whether the parent node is black
if (np->m_color == false) {
m_n++;
return;
}
else {
adjust(n_new);
m_n++;
return;
}
}
void adjust(Node_RB* n) {
//Loop. The parent node of n is not a black node. This is mainly because the uncle node is red, and you can exit the loop when n itself is the root node
while (n != root && n->m_parent->m_color != false) {
if (n->m_parent->m_parent->m_left == n->m_parent) {
//If the parent node is the left node of the grandfather node, consider whether the uncle node exists or not. If not, consider that the insertion node and the parent node are not on the same side
if (n->m_parent->m_parent->m_right == NULL) {
//No uncle node
if (n->m_parent->m_left == n) {
//Both the inserted node and the parent node are left nodes. It's best to change color first and then rotate, otherwise it's not easy to distinguish who is the parent node and who is the inserted node after the rotation
n->m_parent->m_color = false;
n->m_parent->m_parent->m_color = true;
right_rotate(n->m_parent->m_parent);
//If the N - > parent color is black, the loop will exit
}
else {
//The inserted node and the parent node are not on the same side
n->m_color = false;
n->m_parent->m_parent->m_color = true;
left_rotate(n->m_parent);
//Here, the original parent node has become the left child node of the insertion node, so the next step is to rotate right, taking the original grandfather node as the fulcrum
//That is, the parent node of n
right_rotate(n->m_parent);
n = n->m_left;//This step is to exit the loop, so that the parent node of n (actually the original n) is black
}
}
else {
//The node is red
n->m_parent->m_parent->m_color = true;
n->m_parent->m_parent->m_right->m_color = false;
n->m_parent->m_color = false;
//Take grandpa as the insertion node for a new round of loop, or recursion. If Grandpa's parent node is red, it will continue the loop, otherwise it will exit the loop
n = n->m_parent->m_parent;
}
}
else {
//The parent node is the right node
if (n->m_parent->m_parent->m_left == NULL) {
//No uncle node
if (n->m_parent->m_right == n) {
//On the right as the parent node
n->m_parent->m_color = false;
n->m_parent->m_parent->m_color = true;
left_rotate(n->m_parent->m_parent);
}
else {
//Not on the same side
n->m_color = false;
n->m_parent->m_parent->m_color = true;
right_rotate(n->m_parent);
left_rotate(n->m_parent);
n = n->m_right;
}
}
else {
//The node is red
n->m_parent->m_parent->m_color = true;
n->m_parent->m_parent->m_left->m_color = false;
n->m_parent->m_color = false;
n = n->m_parent->m_parent;
}
}
}
//After the loop, remember to set the root to black
root->m_color = false;
}Finally, the more troublesome deletion
Similarly, review the ideas of the previous summary
There are three cases to delete a node
1. The deleted node has two child nodes
In this case, it will change. Find its successor (or predecessor) node, replace the key and value of the successor node, delete the node, and finally change the problem to delete the successor node
Moreover, the successor node is either a leaf node or has only one child node
2. The deleted node has only one child node
This situation is also very simple. There is only one situation, that is, the node is black and has a red child node. If it is a subsequent node, it can only be a right child node
Because other situations do not exist in balance, red and red do not work, black and black, red and black will lead to left-right imbalance
Let the child node replace the node to be deleted, and change the color to black
3. The deleted node is a leaf node
There are two kinds of situations, red or black
1. Red, delete directly
2. Black, very troublesome. Write another function to deal with this situation
//This function is used to find the node of the key
Node_RB* find(int k) {
Node_RB* n = root;
if (n == NULL) {
cout << "no key" << endl;
return n;
}
while (n != NULL) {
if (k < n->m_key) {
n = n->m_left;
}
else if (k > n->m_key) {
n = n->m_right;
}
else {
return n;
}
}
cout << " no key!"<<endl;
return NULL;
}
//This function is used to find the successor node, which is the leftmost point in the right subtree of the current node, that is, the point in the tree that is only larger than the current node
Node_RB* back_node(Node_RB* n) {
if (n == NULL) {
return NULL;
}
else if (n->m_right != NULL) {
//Let's see if there is a right subtree. The current situation must be
n = n->m_right;
//Then cycle to find the leftmost point
while (n->m_left != NULL) {
n = n->m_left;
}
return n; //Find the leftmost point and return
}
else {
//If there is no right subtree, you don't have to look for the root node, otherwise you have to look up
//When n is the left node of the parent node, it means that the parent node is the required successor node
while (n != NULL && n == n->m_parent->m_right) {
n = n->m_parent;
}
return n->m_parent;
}
}
//Delete the node and return the value of this node
string delete_node(int k) {
Node_RB* n = find(k);
if (n != NULL) {
//The node to be deleted was found
if (n->m_left != NULL && n->m_right != NULL) {
//This node has two child nodes, so first find its successor node and let the key and value of the successor node overwrite the original n
//The problem is transformed into deleting subsequent nodes, with only one child node or no child node
Node_RB* n_back = back_node(n);
n->m_key = n_back->m_key;
string temp = n->m_value;
n->m_value = n_back->m_value;
n_back->m_value = temp;
n = n_back;
}
//Judge whether this node has only one child node, and the above if has removed the case of two child nodes
if (n->m_left != NULL || n->m_right != NULL) {
Node_RB* ns = NULL;
if (n->m_left != NULL) {
//There is a left red child node. Let the child node replace the deleted node n
ns = n->m_left;
}
else {
//Right red child node
ns = n->m_right;
}
ns->m_parent = n->m_parent;
if (n->m_parent == NULL) {
//n is root
root = ns;
}
else if (n == n->m_parent->m_left) {
//n is the left node
n->m_parent->m_left = ns;
}
else {
//n is the right node
n->m_parent->m_right = ns;
}
ns->m_color = false;
string old_value = n->m_value;
delete n;
m_n--;
return old_value;
}
else if (n->m_parent == NULL) {
//n is root and has no child nodes
string old_value = n->m_value;
delete n;
m_n--;
return old_value;
}
else {
//n is the leaf node
if (n->m_color == true) {
//If it is a red node, you can delete it directly
if (n->m_parent->m_left == n) {
n->m_parent->m_left = NULL;
}
else {
n->m_parent->m_right = NULL;
}
string old_value = n->m_value;
delete n;
m_n--;
return old_value;
}
else {
//The most troublesome case is the black leaf node, and then write a function to balance it
//In this case, the balance is adjusted first and then deleted
balance_bnode(n);
//After adjustment, delete it again
if (n->m_parent->m_left == n) {
n->m_parent->m_left = NULL;
}
else {
n->m_parent->m_right = NULL;
}
string old_value = n->m_value;
delete n;
m_n--;
return old_value;
}
}
}
else {
return "no key!";
}
}Next, we will handle the function of deleting nodes and black leaf nodes separately
Based on this idea:
In general, because the black node is deleted, it will be unbalanced. Here, it is balanced by borrowing from the brother node, and because it is a black leaf node, there will be brother nodes.
That is, assuming that this node is a left black leaf node to be deleted, it needs to rotate left to let the parent node down to replace it (no matter what color the parent node is originally, it will become its color - Black). At the same time, the brother node (black) will come up to replace the father (become the father's original color), and the right child red node of the brother node will become black to maintain balance.
Other situations will turn into this situation
But if the brother node is also a black leaf node, that is, the brother node has no red sub node, that is, it has no borrowing
It should be noted that the brothers here refer to the brothers in the 2-3-4 tree, so the red brother node in the red black tree is wrong. The sunspot node of the red brother should be turned into the brother node of the deleted node by rotation. See the previous article for details
0. The sibling node is red. By rotating and changing color, the sibling node is black
1. Brother nodes can borrow, that is, they have red child nodes
1. Brother black, son two red
2. Brother black, son Zuo Hong
3. Brother black, son right red
2. Brother nodes can't be borrowed, that is, brother nodes are black leaf nodes
1. If the parent node is red, change the direct parent node to black and the brother node to red
2. If the parent node is black, it is troublesome. If the black depth of the inevitable subtree is to be reduced by 1, it needs to cycle or recursion, going up layer by layer until the root node changes color
void balance_bnode(Node_RB* n) {
//There should be no need to worry that parameter changes will affect the arguments. This is value passing, although there are changes in the while loop n
while (n != root) {
//First, it is divided into left node or right node
if (n->m_parent->m_left == n) {
//n is the left node
//Find the brother node first
Node_RB* nb = n->m_parent->m_right;
//To judge whether it is red or not, it is necessary to operate its child black node to become a new brother node
if (nb->m_color == true) {
nb->m_color = false;
nb->m_parent->m_color = true;
left_rotate(nb->m_parent);
//Set a new sibling node
nb = n->m_parent->m_right;
}
//After finding the sibling node, it is time to judge whether it has child nodes, that is, whether it can be borrowed
if (nb->m_left == NULL && nb->m_right == NULL) {
//Brother node is also a black leaf node. You can't borrow it
//In either case, the sibling node turns red
nb->m_color = true;
if (n->m_parent->m_color == true) {
//1. The parent node is red
n->m_parent->m_color = false;
n = root; //This is to exit the loop
}
else {
//2. The parent node is black
//Then you need to recycle once when the parent node becomes n. of course, if the parent node is the root node, you don't need to cycle
n = n->m_parent;
}
}
else {
//If a sibling node has child nodes that can be borrowed, it will change the situation into a situation with right child red (two child red belong to a situation with right child red)
if (nb->m_right == NULL) {
//A sibling node has no right child node but only a left child node, so it needs to have a right child node through right rotation
nb->m_color = true;
nb->m_left->m_color = false;
right_rotate(nb);
//Now nb becomes the right red child node, and its parent node becomes a new brother node
nb = nb->m_parent;
}
//Now that there are right child red, you need to change the brother node that will replace the parent node to the color of the parent node,
//Replace the parent node of deleted node n with the color of N, black
//The right child of the brother node will go up and turn black to maintain balance
nb->m_color = nb->m_parent->m_color;
nb->m_parent->m_color = false;
nb->m_right->m_color = false;
//Then rotate left with the parent node
left_rotate(n->m_parent);
n = root;//To exit the loop
}
}
else {
//n is the right node
//Find the brother node first
Node_RB* nb = n->m_parent->m_left;
//To judge whether it is red or not, it is necessary to operate its child black node to become a new brother node
if (nb->m_color == true) {
nb->m_color = false;
nb->m_parent->m_color = true;
right_rotate(nb->m_parent);
//Set a new sibling node
nb = n->m_parent->m_left;
}
//After finding the sibling node, it is time to judge whether it has child nodes, that is, whether it can be borrowed
if (nb->m_left == NULL && nb->m_right == NULL) {
//Brother node is also a black leaf node. You can't borrow it
//In either case, the sibling node turns red
nb->m_color = true;
if (n->m_parent->m_color == true) {
//1. The parent node is red
n->m_parent->m_color = false;
n = root; //This is to exit the loop
}
else {
//2. The parent node is black
//Then you need to recycle once when the parent node becomes n. of course, if the parent node is the root node, you don't need to cycle
n = n->m_parent;
}
}
else {
//If a sibling node has child nodes that can be borrowed, the situation will be changed to the situation with left child red (the two child red belong to the situation with left child red)
if (nb->m_left == NULL) {
//The sibling node has no left child node but only right child node, so it needs to have left child node through left rotation
nb->m_color = true;
nb->m_right->m_color = false;
left_rotate(nb);
//Now nb becomes the left red child node, and its parent node becomes a new brother node
nb = nb->m_parent;
}
//Now that the left child is red, you need to change the brother node that will replace the parent node to the color of the parent node,
//Replace the parent node of deleted node n with the color of N, black
//The left child of the brother node will go up and turn black to maintain balance
nb->m_color = nb->m_parent->m_color;
nb->m_parent->m_color = false;
nb->m_left->m_color = false;
//Then rotate with the parent node
right_rotate(n->m_parent);
n = root;//To exit the loop
}
}
}
}Now that the red black tree insertion and deletion code has been written, let's test it.
I use the preamble to traverse and output this tree, including the color of each node
void pre_print() {
queue<int> q1;
queue<bool> q2;
pre_print(root,q1,q2);
int cnt = q1.size();
for (int i = 0; i < cnt; i++) {
cout << q1.front()<<"+"<<q2.front()<<" ";
q1.pop();
q2.pop();
}
cout << endl;
}
void pre_print(Node_RB* n, queue<int> &q1, queue<bool> &q2) {
if (n == NULL) {
return;
}
q1.push(n->m_key);
q2.push(n->m_color);
if (n->m_left!= NULL) {
pre_print(n->m_left,q1,q2);
}
if (n->m_right != NULL) {
pre_print(n->m_right, q1,q2);
}
return;
}Test it. I input 5, 1, 8, 18, 6, 13, 5, 9 and 2 in turn, output it once, then delete 6 and output it again
void test01() {
RB_tree rb;
rb.put(5, "5");
rb.put(1, "1");
rb.put(8, "8");
rb.put(18, "18");
rb.put(6, "6");
rb.put(13, "13");
rb.put(5, "100");
rb.put(9, "9");
rb.put(2, "2");
cout << rb.get_size()<<endl;
cout << "-------------" << endl;
rb.pre_print();
cout << "-------------" << endl;
rb.delete_node(6);
cout << rb.get_size() << endl;
rb.pre_print();
}Output result (preorder traversal):
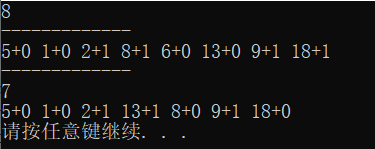
Results generated in the red black tree generation website: Red black tree
Insert:
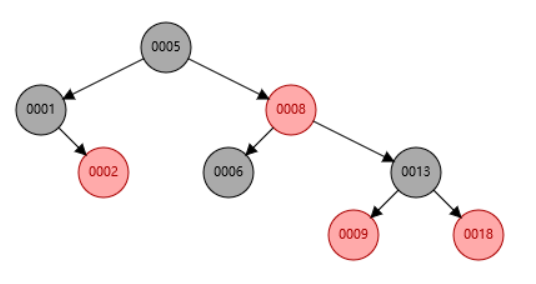
Delete the node with key 6:
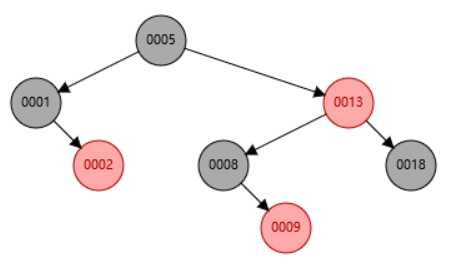
The results are in line with expectations.
Finally, if you have any questions or find errors, welcome to interact in the comment area. I hope this article will be helpful to you!
The complete code is as follows:
#include<iostream>
#include<string>
using namespace std;
#include<queue>
class Node_RB {
public:
int m_key;
string m_value;
bool m_color;
Node_RB* m_left;
Node_RB* m_right;
Node_RB* m_parent;
Node_RB(int k, string v,bool c,Node_RB* l,Node_RB* r,Node_RB* p) {
m_key = k;
m_value = v;
m_color = c;
m_left = l;
m_right = r;
m_parent = p;
}
};
class RB_tree {
public:
Node_RB* root;
int m_n;
RB_tree() {
m_n = 0;
root = NULL;
}
void left_rotate(Node_RB* p) {
// temp = pr; Right node of P = rl; The parent node of rl is set to p; Parent node of PR = parent node of p; The parent node of P is connected to PR; Parent node of P = PR; Left node of PR = p;
Node_RB* temp = p->m_right; //It's pr
p->m_right = temp->m_left;
if (p->m_right != NULL) {
//If rl is not empty, set the parent node of rl to p
p->m_right->m_parent = p;
}
temp->m_parent = p->m_parent; //Is p the left or right node of its parent node, or is it root
if (p->m_parent == NULL) {
//p is the root node
root = temp;
}
else if (p->m_parent->m_left == p) {
//p is the left node
p->m_parent->m_left = temp;
}
else if (p->m_parent->m_right == p) {
//p is the right node
p->m_parent->m_right = temp;
}
p->m_parent = temp;
temp->m_left = p;
}
void right_rotate(Node_RB* p) {
Node_RB* temp = p->m_left; //pl
p->m_left = temp->m_right;
if (p->m_left != NULL) {
p->m_left->m_parent = p;
}
temp->m_parent = p->m_parent;
if (p->m_parent == NULL) {
root = temp;
}
else if (p->m_parent->m_left == p) {
p->m_parent->m_left = temp;
}
else if (p->m_parent->m_right == p) {
p->m_parent->m_right = temp;
}
temp->m_right = p;
p->m_parent = temp;
}
bool get_color(Node_RB* n) {
return n == NULL ? false : n->m_color;
}
int get_size() {
return m_n;
}
void put(int k, string v) {
Node_RB* n = root;
Node_RB* np = root;
if (n == NULL) {
//Insert the first node into the empty tree
root = new Node_RB(k, v, false, NULL, NULL, NULL);
m_n = 1;
return;
}
//Find out where this node is first
while (n != NULL) {
np = n;//Record parent node
if (n->m_key == k) {
//If there is an existing key, just change the value directly
n->m_value = v;
return;
}
else if (k < n->m_key) {
n = n->m_left;
}
else {
n = n->m_right;
}
}
//First, let the parent node of the insertion node point to np
Node_RB* n_new = new Node_RB(k, v, true, NULL, NULL, np);
//Judge whether this node is on the left or right of np
if (k < np->m_key) {
np->m_left = n_new;
}
else {
np->m_right = n_new;
}
//Judge whether the parent node is black
if (np->m_color == false) {
m_n++;
return;
}
else {
adjust(n_new);
m_n++;
return;
}
}
void adjust(Node_RB* n) {
//Loop. The parent node of n is not a black node. This is mainly because the uncle node is red, and you can exit the loop when n itself is the root node
while (n != root && n->m_parent->m_color != false) {
if (n->m_parent->m_parent->m_left == n->m_parent) {
//If the parent node is the left node of the grandfather node, consider whether the uncle node exists or not. If not, consider that the insertion node and the parent node are not on the same side
if (n->m_parent->m_parent->m_right == NULL) {
//No uncle node
if (n->m_parent->m_left == n) {
//Both the inserted node and the parent node are left nodes. It's best to change color first and then rotate, otherwise it's not easy to distinguish who is the parent node and who is the inserted node after the rotation
n->m_parent->m_color = false;
n->m_parent->m_parent->m_color = true;
right_rotate(n->m_parent->m_parent);
//If the N - > parent color is black, the loop will exit
}
else {
//The inserted node and the parent node are not on the same side
n->m_color = false;
n->m_parent->m_parent->m_color = true;
left_rotate(n->m_parent);
//Here, the original parent node has become the left child node of the insertion node, so the next step is to rotate right, taking the original grandfather node as the fulcrum
//That is, the parent node of n
right_rotate(n->m_parent);
n = n->m_left;//This step is to exit the loop, so that the parent node of n (actually the original n) is black
}
}
else {
//The node is red
n->m_parent->m_parent->m_color = true;
n->m_parent->m_parent->m_right->m_color = false;
n->m_parent->m_color = false;
//Take grandpa as the insertion node for a new round of loop, or recursion. If Grandpa's parent node is red, it will continue the loop, otherwise it will exit the loop
n = n->m_parent->m_parent;
}
}
else {
//The parent node is the right node
if (n->m_parent->m_parent->m_left == NULL) {
//No uncle node
if (n->m_parent->m_right == n) {
//On the right as the parent node
n->m_parent->m_color = false;
n->m_parent->m_parent->m_color = true;
left_rotate(n->m_parent->m_parent);
}
else {
//Not on the same side
n->m_color = false;
n->m_parent->m_parent->m_color = true;
right_rotate(n->m_parent);
left_rotate(n->m_parent);
n = n->m_right;
}
}
else {
//The node is red
n->m_parent->m_parent->m_color = true;
n->m_parent->m_parent->m_left->m_color = false;
n->m_parent->m_color = false;
n = n->m_parent->m_parent;
}
}
}
//After the loop, remember to set the root to black
root->m_color = false;
}
void pre_print() {
queue<int> q1;
queue<bool> q2;
pre_print(root,q1,q2);
int cnt = q1.size();
for (int i = 0; i < cnt; i++) {
cout << q1.front()<<"+"<<q2.front()<<" ";
q1.pop();
q2.pop();
}
cout << endl;
}
void pre_print(Node_RB* n, queue<int> &q1, queue<bool> &q2) {
if (n == NULL) {
return;
}
q1.push(n->m_key);
q2.push(n->m_color);
if (n->m_left!= NULL) {
pre_print(n->m_left,q1,q2);
}
if (n->m_right != NULL) {
pre_print(n->m_right, q1,q2);
}
return;
}
/*void find(int k) {
find(root,k);
}*/
Node_RB* find(int k) {
Node_RB* n = root;
if (n == NULL) {
cout << "no key" << endl;
return n;
}
while (n != NULL) {
if (k < n->m_key) {
n = n->m_left;
}
else if (k > n->m_key) {
n = n->m_right;
}
else {
return n;
}
}
cout << " no key!"<<endl;
return NULL;
}
string delete_node(int k) {
Node_RB* n = find(k);
if (n != NULL) {
//The node to be deleted was found
if (n->m_left != NULL && n->m_right != NULL) {
//This node has two child nodes, so first find its successor node and let the key and value of the successor node overwrite the original n
//The problem is transformed into deleting subsequent nodes, with only one child node or no child node
Node_RB* n_back = back_node(n);
n->m_key = n_back->m_key;
string temp = n->m_value;
n->m_value = n_back->m_value;
n_back->m_value = temp;
n = n_back;
}
//Judge whether this node has only one child node, and the above if has removed the case of two child nodes
if (n->m_left != NULL || n->m_right != NULL) {
Node_RB* ns = NULL;
if (n->m_left != NULL) {
//There is a left red child node. Let the child node replace the deleted node n
ns = n->m_left;
}
else {
//Right red child node
ns = n->m_right;
}
ns->m_parent = n->m_parent;
if (n->m_parent == NULL) {
//n is root
root = ns;
}
else if (n == n->m_parent->m_left) {
//n is the left node
n->m_parent->m_left = ns;
}
else {
//n is the right node
n->m_parent->m_right = ns;
}
ns->m_color = false;
string old_value = n->m_value;
delete n;
m_n--;
return old_value;
}
else if (n->m_parent == NULL) {
//n is root and has no child nodes
string old_value = n->m_value;
delete n;
m_n--;
return old_value;
}
else {
//n is the leaf node
if (n->m_color == true) {
//If it is a red node, you can delete it directly
if (n->m_parent->m_left == n) {
n->m_parent->m_left = NULL;
}
else {
n->m_parent->m_right = NULL;
}
string old_value = n->m_value;
delete n;
m_n--;
return old_value;
}
else {
//The most troublesome case is the black leaf node, and then write a function to balance it
//In this case, the balance is adjusted first and then deleted
balance_bnode(n);
//After adjustment, delete it again
if (n->m_parent->m_left == n) {
n->m_parent->m_left = NULL;
}
else {
n->m_parent->m_right = NULL;
}
string old_value = n->m_value;
delete n;
m_n--;
return old_value;
}
}
}
else {
return "no key!";
}
}
void balance_bnode(Node_RB* n) {
//There should be no need to worry that parameter changes will affect the arguments. This is value passing, although there are changes in the while loop n
while (n != root) {
//First, it is divided into left node or right node
if (n->m_parent->m_left == n) {
//n is the left node
//Find the brother node first
Node_RB* nb = n->m_parent->m_right;
//To judge whether it is red or not, it is necessary to operate its child black node to become a new brother node
if (nb->m_color == true) {
nb->m_color = false;
nb->m_parent->m_color = true;
left_rotate(nb->m_parent);
//Set a new sibling node
nb = n->m_parent->m_right;
}
//After finding the sibling node, it is time to judge whether it has child nodes, that is, whether it can be borrowed
if (nb->m_left == NULL && nb->m_right == NULL) {
//Brother node is also a black leaf node. You can't borrow it
//In either case, the sibling node turns red
nb->m_color = true;
if (n->m_parent->m_color == true) {
//1. The parent node is red
n->m_parent->m_color = false;
n = root; //This is to exit the loop
}
else {
//2. The parent node is black
//Then you need to recycle once when the parent node becomes n. of course, if the parent node is the root node, you don't need to cycle
n = n->m_parent;
}
}
else {
//If a sibling node has child nodes that can be borrowed, it will change the situation into a situation with right child red (two child red belong to a situation with right child red)
if (nb->m_right == NULL) {
//A sibling node has no right child node but only a left child node, so it needs to have a right child node through right rotation
nb->m_color = true;
nb->m_left->m_color = false;
right_rotate(nb);
//Now nb becomes the right red child node, and its parent node becomes a new brother node
nb = nb->m_parent;
}
//Now that there are right child red, you need to change the brother node that will replace the parent node to the color of the parent node,
//Replace the parent node of deleted node n with the color of N, black
//The right child of the brother node will go up and turn black to maintain balance
nb->m_color = nb->m_parent->m_color;
nb->m_parent->m_color = false;
nb->m_right->m_color = false;
//Then rotate left with the parent node
left_rotate(n->m_parent);
n = root;//To exit the loop
}
}
else {
//n is the right node
//Find the brother node first
Node_RB* nb = n->m_parent->m_left;
//To judge whether it is red or not, it is necessary to operate its child black node to become a new brother node
if (nb->m_color == true) {
nb->m_color = false;
nb->m_parent->m_color = true;
right_rotate(nb->m_parent);
//Set a new sibling node
nb = n->m_parent->m_left;
}
//After finding the sibling node, it is time to judge whether it has child nodes, that is, whether it can be borrowed
if (nb->m_left == NULL && nb->m_right == NULL) {
//Brother node is also a black leaf node. You can't borrow it
//In either case, the sibling node turns red
nb->m_color = true;
if (n->m_parent->m_color == true) {
//1. The parent node is red
n->m_parent->m_color = false;
n = root; //This is to exit the loop
}
else {
//2. The parent node is black
//Then you need to recycle once when the parent node becomes n. of course, if the parent node is the root node, you don't need to cycle
n = n->m_parent;
}
}
else {
//If a sibling node has child nodes that can be borrowed, the situation will be changed to the situation with left child red (the two child red belong to the situation with left child red)
if (nb->m_left == NULL) {
//The sibling node has no left child node but only right child node, so it needs to have left child node through left rotation
nb->m_color = true;
nb->m_right->m_color = false;
left_rotate(nb);
//Now nb becomes the left red child node, and its parent node becomes a new brother node
nb = nb->m_parent;
}
//Now that the left child is red, you need to change the brother node that will replace the parent node to the color of the parent node,
//Replace the parent node of deleted node n with the color of N, black
//The left child of the brother node will go up and turn black to maintain balance
nb->m_color = nb->m_parent->m_color;
nb->m_parent->m_color = false;
nb->m_left->m_color = false;
//Then rotate with the parent node
right_rotate(n->m_parent);
n = root;//To exit the loop
}
}
}
}
Node_RB* back_node(Node_RB* n) {
if (n == NULL) {
return NULL;
}
else if (n->m_right != NULL) {
//Let's see if there is a right subtree. The current situation must be
n = n->m_right;
//Then cycle to find the leftmost point
while (n->m_left != NULL) {
n = n->m_left;
}
return n; //Find the leftmost point and return
}
else {
//If there is no right subtree, you don't have to look for the root node, otherwise you have to look up
//When n is the left node of the parent node, it means that the parent node is the required successor node
while (n != NULL && n == n->m_parent->m_right) {
n = n->m_parent;
}
return n->m_parent;
}
}
};
void test01() {
RB_tree rb;
rb.put(5, "5");
rb.put(1, "1");
rb.put(8, "8");
rb.put(18, "18");
rb.put(6, "6");
rb.put(13, "13");
rb.put(5, "100");
rb.put(9, "9");
rb.put(2, "2");
cout << rb.get_size()<<endl;
cout << "-------------" << endl;
rb.pre_print();
cout << "-------------" << endl;
rb.delete_node(6);
cout << rb.get_size() << endl;
rb.pre_print();
}
int main() {
test01();
system("pause");
return 0;
}