Original Address

https://www.cnblogs.com/CarpenterLee/p/5503882.html

Previous to this article

• Reviewing data structures: common binary tree methods and three traversal methods Java implementation https://blog.csdn.net/u011240877/article/details/53193918
• Reviewing data structure: finding, inserting, deleting binary sort trees https://blog.csdn.net/u011240877/article/details/53242179
• Re-examining data structures: A deeper understanding of red and black trees https://blog.csdn.net/u011240877/article/details/53329023

Overall introduction

• Java TreeMap implements the SortedMap interface, which means elements in the Map are sorted by the size order of the key, which can be judged either by its own natural ordering or by the Comparator passed in when it was constructed.

• The underlying TreeMap is implemented through a Red-Black tree, which means that containsKey(), get(), put(), remove() all have log(n) time complexity.The algorithm implementation refers to the Introduction to Algorithms.

• For performance reasons, TreeMap is not synchronized, and programmers need to synchronize it manually if they need to be used in a multithreaded environment, or wrapped it to be synchronized as follows:

SortedMap m = Collections.synchronizedSortedMap(new TreeMap(…));

• A red-black tree is an approximately balanced binary lookup tree that ensures that the height difference between the left and right subtrees of any node does not exceed that of the lower one.Specifically, a red-black tree is a binary search tree that meets the following criteria:

  • Each node is either red or black
  • Root node must be black
  • Red nodes cannot be continuous (that is, neither children nor fathers of red nodes can be red)
  • For each node, any path from that point to null (the end of the tree) contains the same number of black nodes

• When the structure of the tree changes (insert or delete operations), the above conditions 3 or 4 are often destroyed, and the search tree needs to be adjusted to meet the conditions of the red-black tree again.

• When the structure of the search tree changes, the conditions of the red-black tree may be destroyed, and the search tree needs to be adjusted to meet the conditions of the red-black tree again.Adjustments can be divided into two categories: one is color adjustment, which changes the color of a node; the other is structure adjustment, which changes the structure relationship of the retrieval tree.The structural adjustment process consists of two basic operations: Rotate Left and Rotate Right.

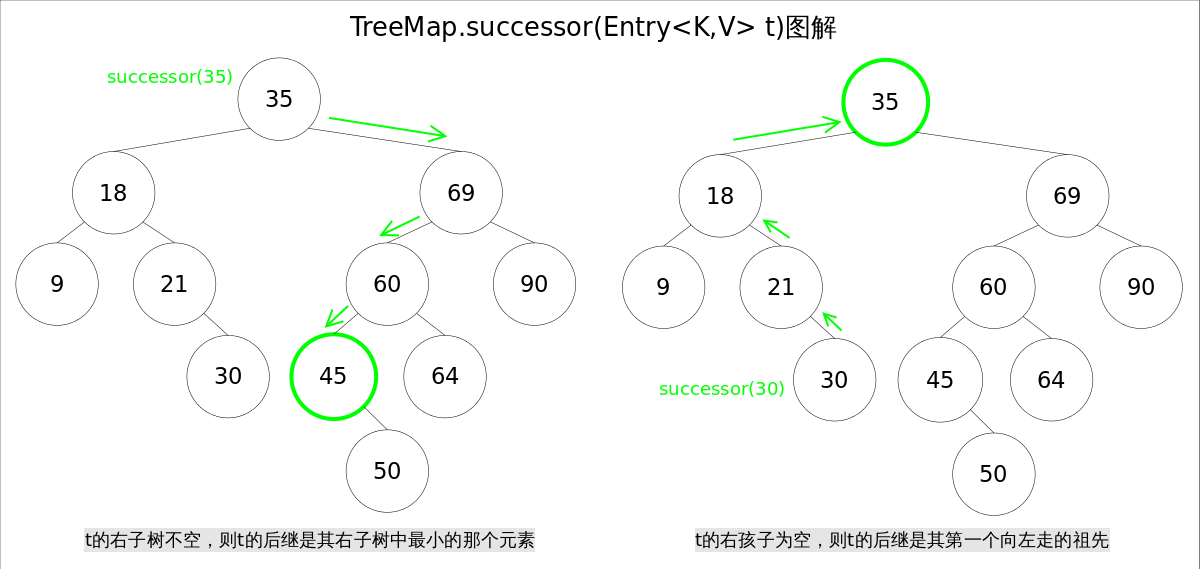
• Find Node Successors

For a binary lookup tree, given node t, its successors (the smallest element with a tree species greater than t) can be found as follows:

• Left-handed
  The left-handed process rotates the right subtree of X counterclockwise around x, making the right subtree of x the father of x, and modifying the reference of the related node.After rotation, the properties of the binary lookup tree are still satisfied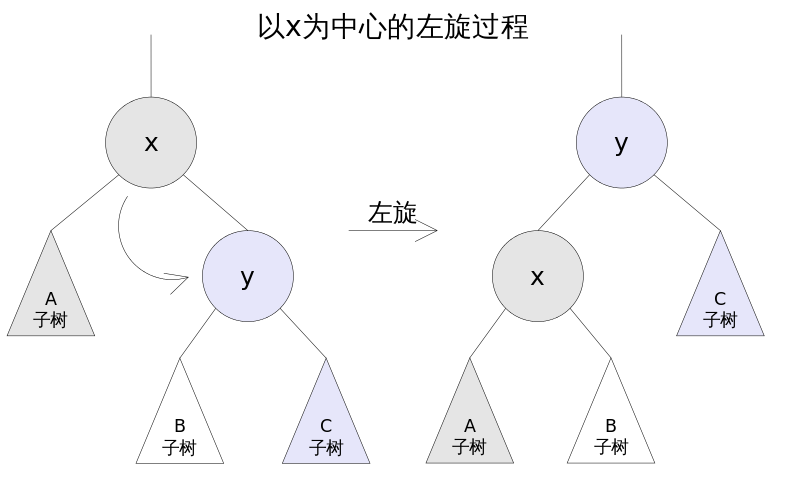
  
  The left-hand code in TreeMap is as follows:

//Rotate Left
private void rotateLeft(Entry<K,V> p) {
    if (p != null) {
        Entry<K,V> r = p.right;
        p.right = r.left;
        if (r.left != null)
            r.left.parent = p;
        r.parent = p.parent;
        if (p.parent == null)
            root = r;
        else if (p.parent.left == p)
            p.parent.left = r;
        else
            p.parent.right = r;
        r.left = p;
        p.parent = r;
    }
}

• Right Hand
  The right-hand process rotates the left subtree of X clockwise around x, making the left subtree of x the father of x, and modifying the reference of the related node.After rotation, the properties of the binary search tree are still satisfied.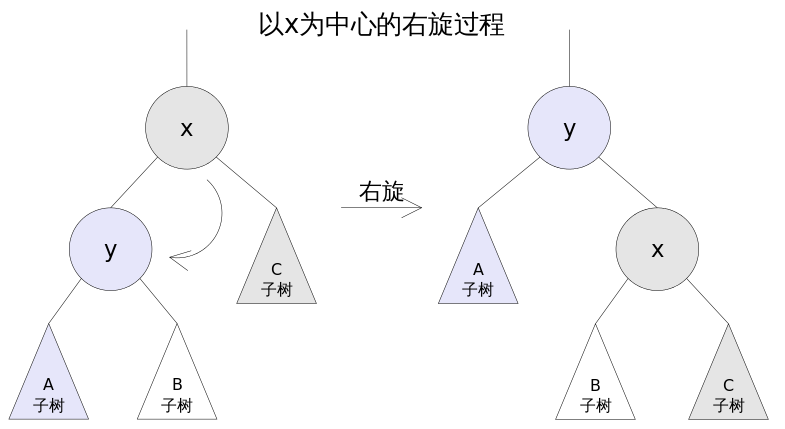
  
  The right-hand code in TreeMap is as follows:

//Rotate Right
private void rotateRight(Entry<K,V> p) {
    if (p != null) {
        Entry<K,V> l = p.left;
        p.left = l.right;
        if (l.right != null) l.right.parent = p;
        l.parent = p.parent;
        if (p.parent == null)
            root = l;
        else if (p.parent.right == p)
            p.parent.right = l;
        else p.parent.left = l;
        l.right = p;
        p.parent = l;
    }
}

get() parsing

The get(Object key) method returns the corresponding value based on the specified key value, which calls getEntry(Object key) to get the corresponding entry and then returns entry.value.getEntry() is therefore the core of the algorithm.The idea is to find binary lookup trees in the natural order of keys (or comparator order) until an entry satisfying k.compareTo(p.key) == 0 is found.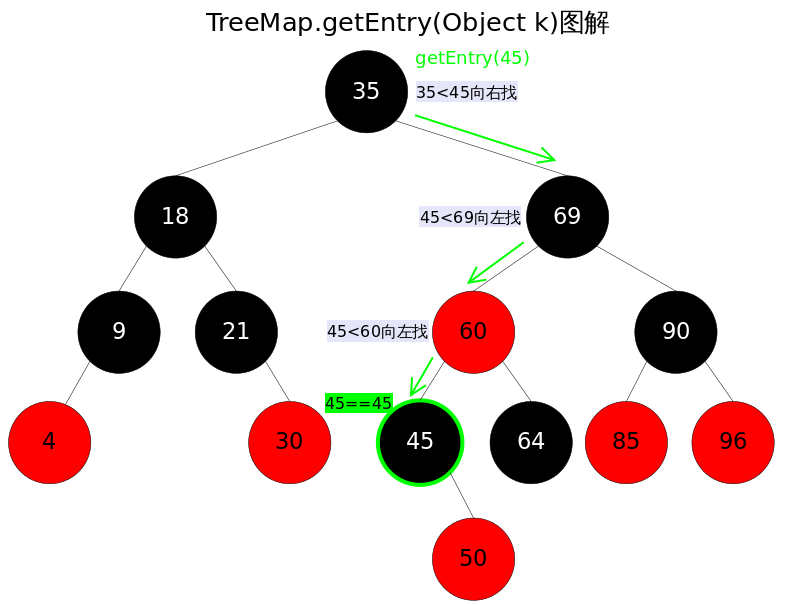

The code is as follows:

//getEntry() method
final Entry<K,V> getEntry(Object key) {
    ......
    if (key == null)//key value is not allowed to be null
        throw new NullPointerException();
    Comparable<? super K> k = (Comparable<? super K>) key;//Use the natural order of elements
    Entry<K,V> p = root;
    while (p != null) {
        int cmp = k.compareTo(p.key);
        if (cmp < 0)//Look Left
            p = p.left;
        else if (cmp > 0)//Look right
            p = p.right;
        else
            return p;
    }
    return null;
}

put() parsing

The put(K key, V value) method adds the specified key, value pair to the map.This method first looks for the map to see if it contains the tuple, and returns directly if it already contains it, similar to the getEntry() method; if it is not found, it inserts a new entry into the red-black tree, and if it breaks the constraints of the red-black tree after insertion, it also needs to adjust (rotate, change the color of some nodes)

public V put(K key, V value) {
    ......
    int cmp;
    Entry<K,V> parent;
    if (key == null)
        throw new NullPointerException();
    Comparable<? super K> k = (Comparable<? super K>) key;//Use the natural order of elements
    do {
        parent = t;
        cmp = k.compareTo(t.key);
        if (cmp < 0) t = t.left;//Look Left
        else if (cmp > 0) t = t.right;//Look right
        else return t.setValue(value);
    } while (t != null);
    Entry<K,V> e = new Entry<>(key, value, parent);//Create and insert a new entry
    if (cmp < 0) parent.left = e;
    else parent.right = e;
    fixAfterInsertion(e);//adjustment
    size++;
    return null;
}

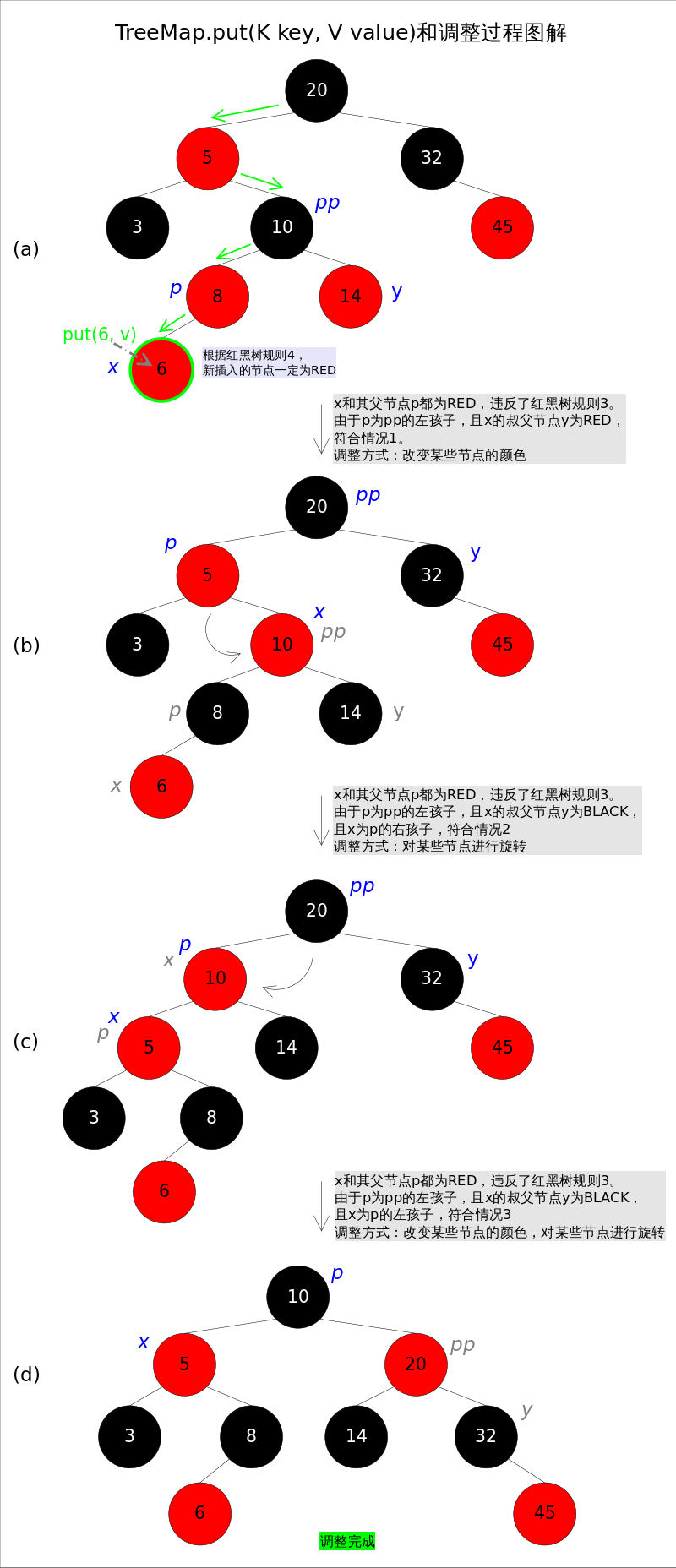
The code for the tuning function fixAfterInsertion() is as follows, using the rotateLeft() and rotateRight() functions mentioned above.As we can see from the code, scenario 2 actually falls within scenario 3.Scenarios 4-6 are symmetrical with the first three, so the last three are not drawn in the illustration. Readers can refer to the code for their own understanding.

//fixAfterInsertion()
private void fixAfterInsertion(Entry<K,V> x) {
    x.color = RED;
    while (x != null && x != root && x.parent.color == RED) {
        if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
            Entry<K,V> y = rightOf(parentOf(parentOf(x)));
            if (colorOf(y) == RED) {//If y is null, it is treated as BLACK
                setColor(parentOf(x), BLACK);              // Situation 1
                setColor(y, BLACK);                        // Situation 1
                setColor(parentOf(parentOf(x)), RED);      // Situation 1
                x = parentOf(parentOf(x));                 // Situation 1
            } else {
                if (x == rightOf(parentOf(x))) {
                    x = parentOf(x);                       // Situation 2
                    rotateLeft(x);                         // Situation 2
                }
                setColor(parentOf(x), BLACK);              // Situation 3
                setColor(parentOf(parentOf(x)), RED);      // Situation 3
                rotateRight(parentOf(parentOf(x)));        // Situation 3
            }
        } else {
            Entry<K,V> y = leftOf(parentOf(parentOf(x)));
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);              // Situation 4
                setColor(y, BLACK);                        // Situation 4
                setColor(parentOf(parentOf(x)), RED);      // Situation 4
                x = parentOf(parentOf(x));                 // Situation 4
            } else {
                if (x == leftOf(parentOf(x))) {
                    x = parentOf(x);                       // Situation 5
                    rotateRight(x);                        // Situation 5
                }
                setColor(parentOf(x), BLACK);              // Situation 6
                setColor(parentOf(parentOf(x)), RED);      // Situation 6
                rotateLeft(parentOf(parentOf(x)));         // Situation 6
            }
        }
    }
    root.color = BLACK;
}

remove() parsing

• The purpose of remove(Object key) is to delete the entry corresponding to the key value, which first finds the entry corresponding to the key value through the getEntry(Object key) method mentioned above, then calls deleteEntry (Entry<K, V> entry) to delete the corresponding entry.Since deletion alters the structure of the red-black tree, potentially breaking its constraints, adjustments may be made.
• Since the red-black tree is an enhanced version of the binary search tree, the deletion of the red-black tree is very similar to the deletion of the ordinary binary search tree. The only difference is that the red-black tree may need to be adjusted after the node is deleted.Now consider the deletion of an ordinary binary search tree, which can be divided into two simple cases:

Based on the above logic, the node deletion function deleteEntry() of the red-black tree is coded as follows:

// Red-black tree entry delete function deleteEntry()
private void deleteEntry(Entry<K,V> p) {
    modCount++;
    size--;
    if (p.left != null && p.right != null) {// 2. Neither left nor right subtree of delete point p is empty.
        Entry<K,V> s = successor(p);// Subsequent
        p.key = s.key;
        p.value = s.value;
        p = s;
    }
    Entry<K,V> replacement = (p.left != null ? p.left : p.right);
    if (replacement != null) {// 1.Delete point p has only one subtree that is not empty.
        replacement.parent = p.parent;
        if (p.parent == null)
            root = replacement;
        else if (p == p.parent.left)
            p.parent.left  = replacement;
        else
            p.parent.right = replacement;
        p.left = p.right = p.parent = null;
        if (p.color == BLACK)
            fixAfterDeletion(replacement);// adjustment
    } else if (p.parent == null) {
        root = null;
    } else { // 1. The left and right subtrees of deletion point p are empty
        if (p.color == BLACK)
            fixAfterDeletion(p);// adjustment
        if (p.parent != null) {
            if (p == p.parent.left)
                p.parent.left = null;
            else if (p == p.parent.right)
                p.parent.right = null;
            p.parent = null;
        }
    }
}

The logic of the code used to modify reference relationships between parent and child nodes is not difficult to understand.The following highlights the deleted adjustment function fixAfterDeletion().

First, think about what points have been deleted to make the adjustment?The adjustment function will only be triggered if the deletion point is a BLACK, because deleting the RED node will not break any constraints on the red-black tree, and deleting the BLACK node will break Rule 4.

Like the fixAfterInsertion() function described above, there are several cases here.Remember, no matter how many cases there are, there are only two specific adjustments:

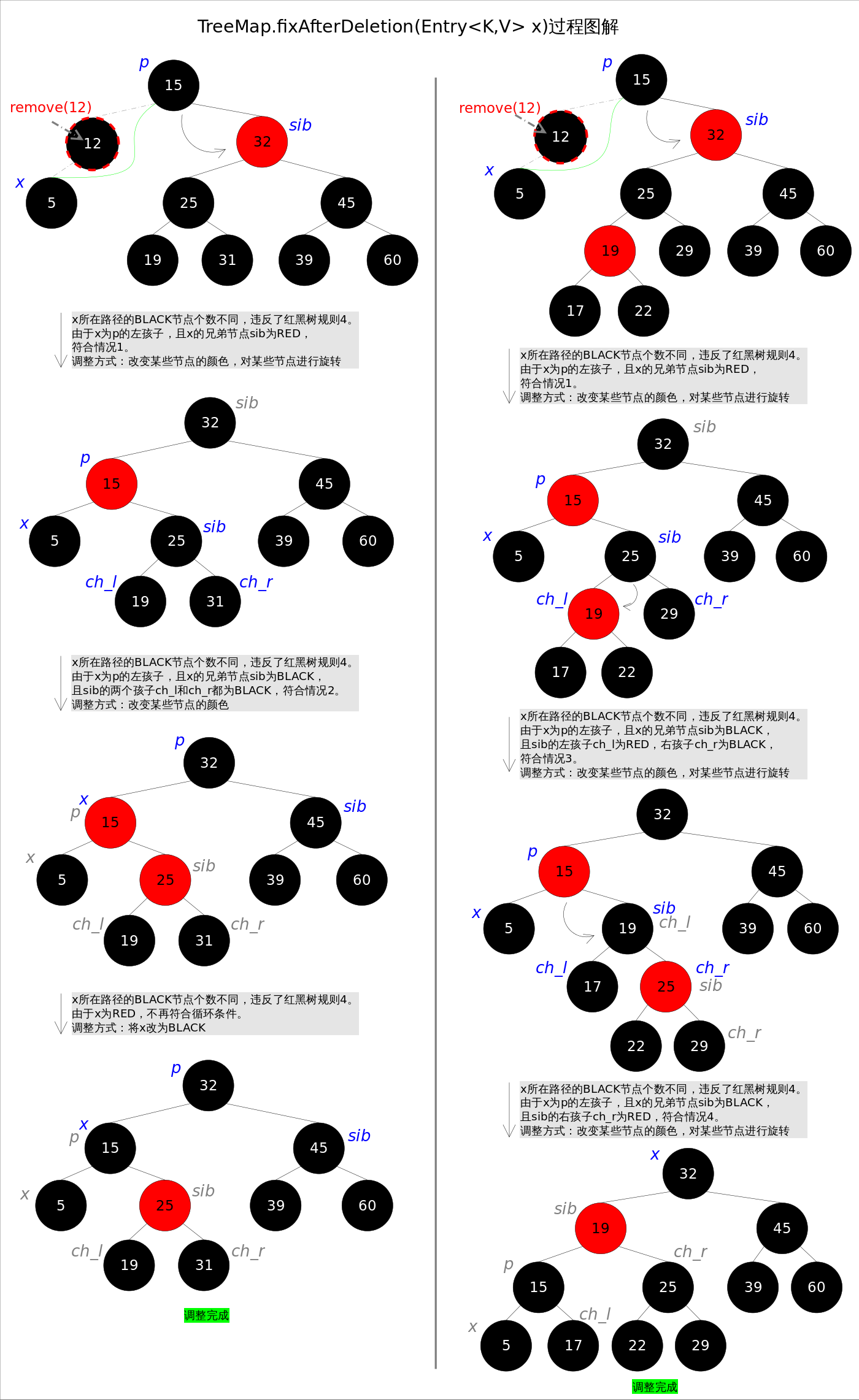
The general idea of the illustrations above is to convert scenario 1 to scenario 2 first, or to scenarios 3 and 4.Of course, this illustration does not mean that the adjustment process must start in case 1.We will also find several interesting rules in the following code: a) if case 1 followed by case 2, then case 2 must exit the loop (because x is red); and b) if case 3 and case 4 are entered, the loop must exit (because x is root).

The code for the deleted adjustment function fixAfterDeletion() is as follows, using the rotateLeft() and rotateRight() functions mentioned above.As we can see from the code, scenario 3 actually falls within scenario 4.The first four cases in scenarios 5-8 are symmetrical, so the last four cases are not drawn in the illustration. Readers can refer to the code to understand them.

private void fixAfterDeletion(Entry<K,V> x) {
    while (x != root && colorOf(x) == BLACK) {
        if (x == leftOf(parentOf(x))) {
            Entry<K,V> sib = rightOf(parentOf(x));
            if (colorOf(sib) == RED) {
                setColor(sib, BLACK);                   // Situation 1
                setColor(parentOf(x), RED);             // Situation 1
                rotateLeft(parentOf(x));                // Situation 1
                sib = rightOf(parentOf(x));             // Situation 1
            }
            if (colorOf(leftOf(sib))  == BLACK &&
                colorOf(rightOf(sib)) == BLACK) {
                setColor(sib, RED);                     // Situation 2
                x = parentOf(x);                        // Situation 2
            } else {
                if (colorOf(rightOf(sib)) == BLACK) {
                    setColor(leftOf(sib), BLACK);       // Situation 3
                    setColor(sib, RED);                 // Situation 3
                    rotateRight(sib);                   // Situation 3
                    sib = rightOf(parentOf(x));         // Situation 3
                }
                setColor(sib, colorOf(parentOf(x)));    // Situation 4
                setColor(parentOf(x), BLACK);           // Situation 4
                setColor(rightOf(sib), BLACK);          // Situation 4
                rotateLeft(parentOf(x));                // Situation 4
                x = root;                               // Situation 4
            }
        } else { // Symmetrical to the first four cases
            Entry<K,V> sib = leftOf(parentOf(x));
            if (colorOf(sib) == RED) {
                setColor(sib, BLACK);                   // Situation 5
                setColor(parentOf(x), RED);             // Situation 5
                rotateRight(parentOf(x));               // Situation 5
                sib = leftOf(parentOf(x));              // Situation 5
            }
            if (colorOf(rightOf(sib)) == BLACK &&
                colorOf(leftOf(sib)) == BLACK) {
                setColor(sib, RED);                     // Situation 6
                x = parentOf(x);                        // Situation 6
            } else {
                if (colorOf(leftOf(sib)) == BLACK) {
                    setColor(rightOf(sib), BLACK);      // Situation 7
                    setColor(sib, RED);                 // Situation 7
                    rotateLeft(sib);                    // Situation 7
                    sib = leftOf(parentOf(x));          // Situation 7
                }
                setColor(sib, colorOf(parentOf(x)));    // Situation 8
                setColor(parentOf(x), BLACK);           // Situation 8
                setColor(leftOf(sib), BLACK);           // Situation 8
                rotateRight(parentOf(x));               // Situation 8
                x = root;                               // Situation 8
            }
        }
    }
    setColor(x, BLACK);
}

TreeSet

TreeSet is a simple wrapper of TeeMap, and all function calls to TreeSet are converted to the appropriate TeeMap method

// TreeSet is a simple wrapper for TreeMap
public class TreeSet<E> extends AbstractSet<E>
    implements NavigableSet<E>, Cloneable, java.io.Serializable
{
    ......
    private transient NavigableMap<E,Object> m;
    // Dummy value to associate with an Object in the backing Map
    private static final Object PRESENT = new Object();
    public TreeSet() {
        this.m = new TreeMap<E,Object>();// There is a TreeMap inside the TreeSet
    }
    ......
    public boolean add(E e) {
        return m.put(e, PRESENT)==null;
    }
    ......
}

Thank you for reading this blog!!!