balanced binary tree
In order to avoid the phenomenon of "lameness", reduce the height of the tree and improve our search efficiency, there is another tree structure: "balanced binary tree" is called AVl tree on the right
Rule: the absolute value of the height difference between the left and right subtrees is no more than 1, and both the left and right subtrees are a balanced binary tree
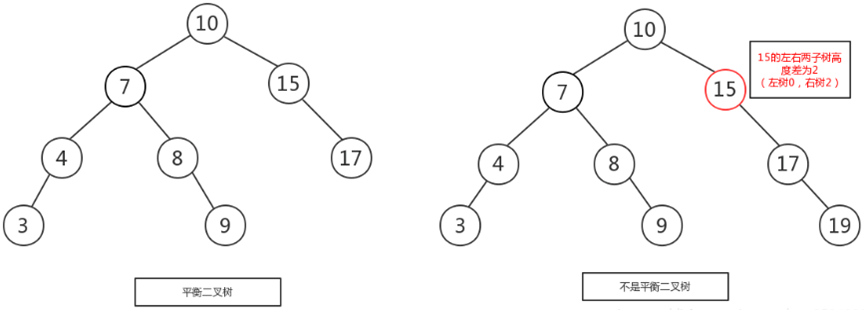
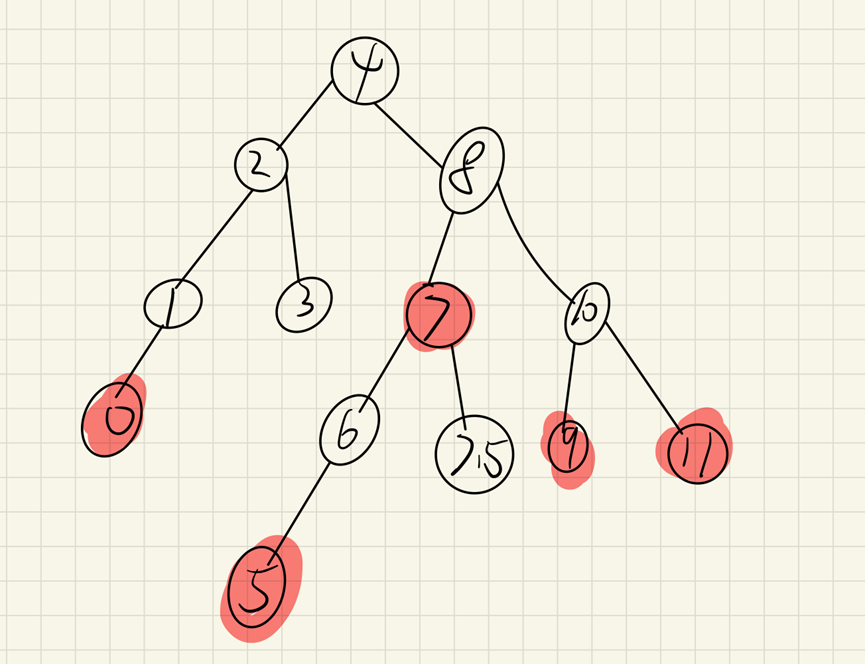
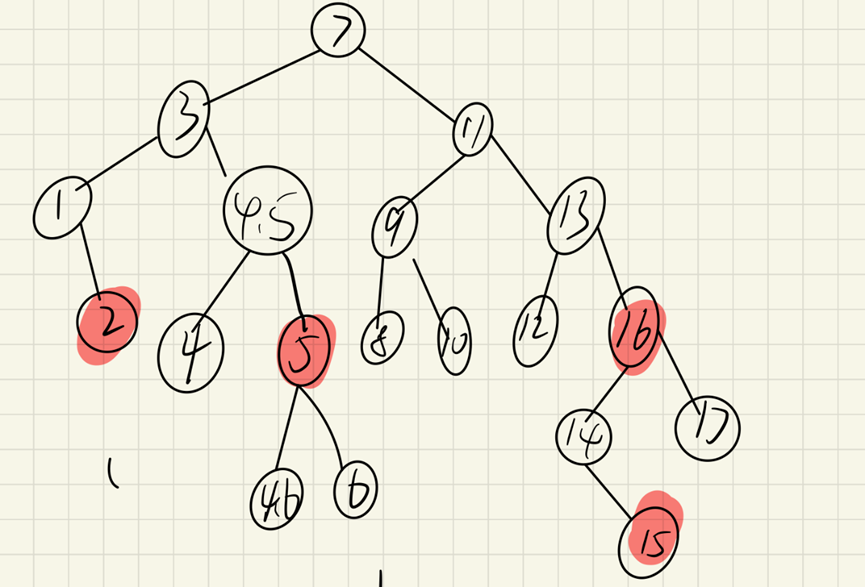
In the above figure, the left figure is a balanced binary tree, while in the right figure, although the height difference between the left and right subtrees of the root node is 0, the height difference between the left and right words of the right subtree 15 is 2, which does not conform to the nature of a balanced binary tree, so the right figure is not an AVL tree
How to convert the similar situation in the right figure into an AVL tree?
Rotation is introduced to solve this problem
rotate
In the process of building a balanced binary tree, when there are new nodes to be inserted, check whether the balance of the tree is damaged due to the insertion. If so, rotate to change the structure of the tree.
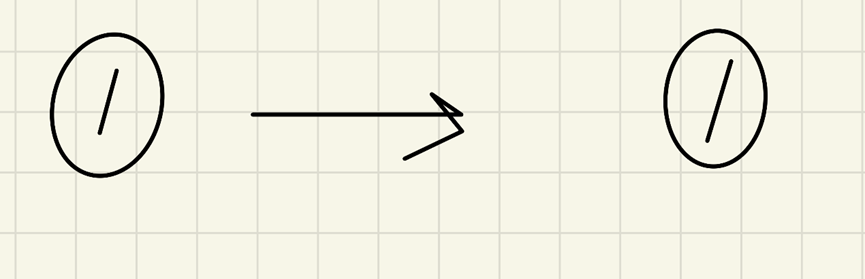
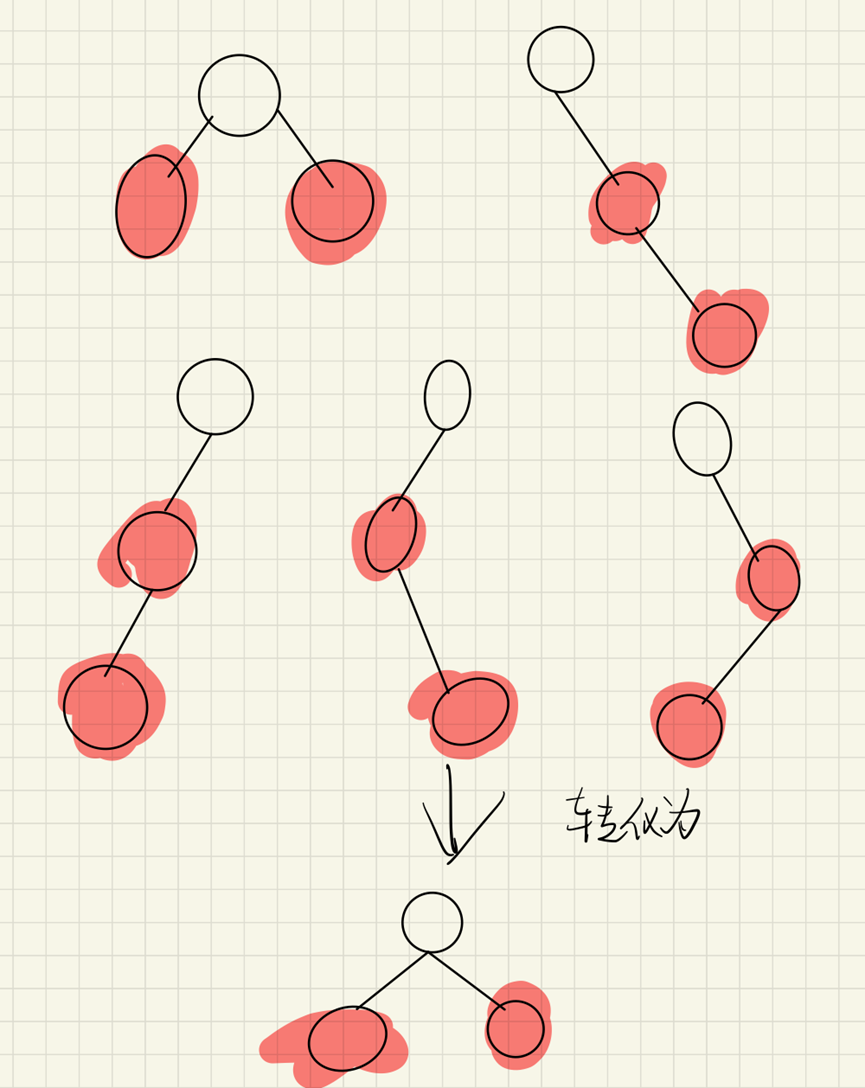
Left hand rotation:
Left rotation is to pull the right branch of the node to the left, turn the right child node into the parent node, and transfer the redundant left child node after promotion to the right child node of the degraded node;
/**
* left-handed
* p pr
* / \ / \
* pl pr p rr
* / \ / \
* rl rr pl rl
*/
Code implementation:
public void leftRotate(RBNode p){
if(p!=null){
RBNode r = p.right;
//PR RL becomes p-rl
p.right = r.left;
if (r.left!=null){
r.left.parent = p;
}
//Determine whether p has a parent node
r.parent = p.parent;
if (p.parent == null){
root = r;
}else if (p.parent.left ==p){
p.parent.left = r;
}else {
p.parent.right = r;
}
//Finally, set p as the left child node of r
r.left = p;
p.parent = r;
}
}Right hand rotation:
Pull the left branch of the node to the right, the left child node becomes the parent node, and transfer the redundant right child node after promotion to the left child node of the degraded node
/**
* right handed
* pf pf
* \ \
* p (l)pl
* / \ => / \
*(l)pl pr ll p
* / \ / \
* ll lr lr pr
*
code implementation
private void rightRotate(RBNode p) {
if (p != null) {
RBNode l = p.left;
p.left = l.right;
if (l.right != null) {
l.right.parent = p;
}
l.parent = p.parent;
if (p.parent == null) {
root = l;
} else if (p.parent.right == p) {
p.parent.right = l;
} else {
p.parent.left = l;
}
l.right = p;
p.parent = l;
}
}When building a balanced binary tree, when a new node is inserted, it will be judged that it is balanced after insertion, which shows that it is balanced before inserting a new node, that is, the absolute value of height difference will not exceed 1. When a new node is inserted,
There may be tree imbalance, which needs to be adjusted. There are four possible situations, namely left, left, right, left and right.
Left left
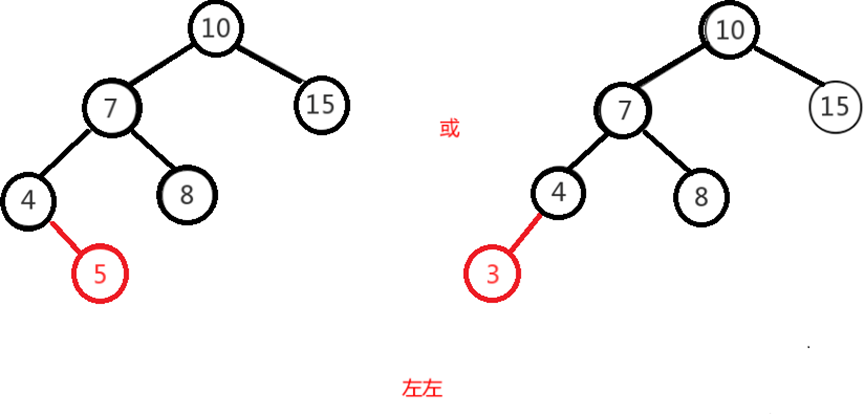
Left means that on the original balanced binary tree, a new node is inserted under the left subtree of the left subtree of the node, resulting in a height difference of 2 between the left and right subtrees of the node, as follows: the left subtree of "10" node is "7", the left subtree of "4", and the insertion of node "5" or "3" leads to imbalance
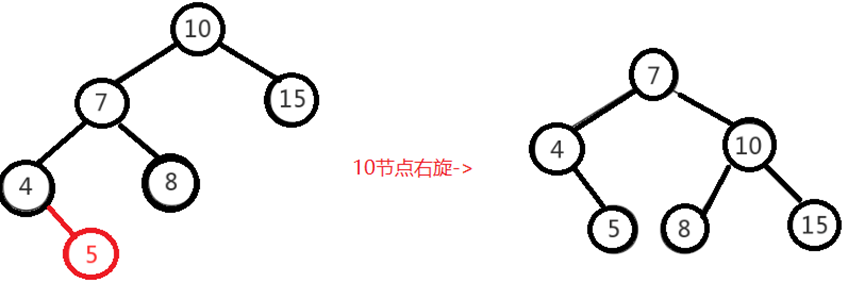
Left left adjustment is actually relatively simple. You only need to rotate the node right. As shown in the figure below, rotate the node "10" right,
about
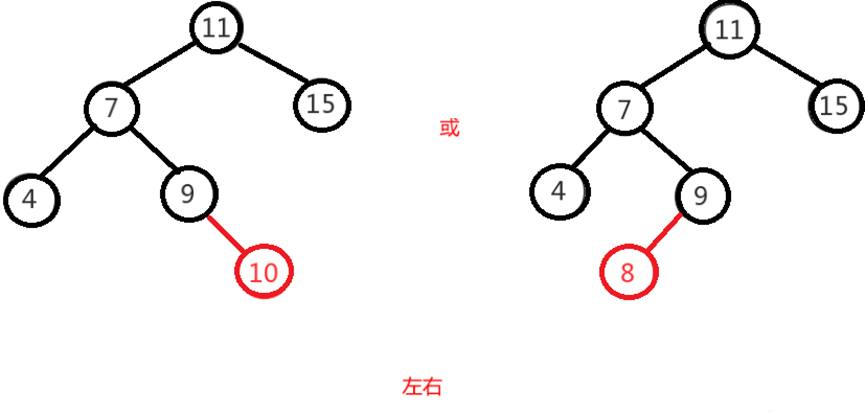
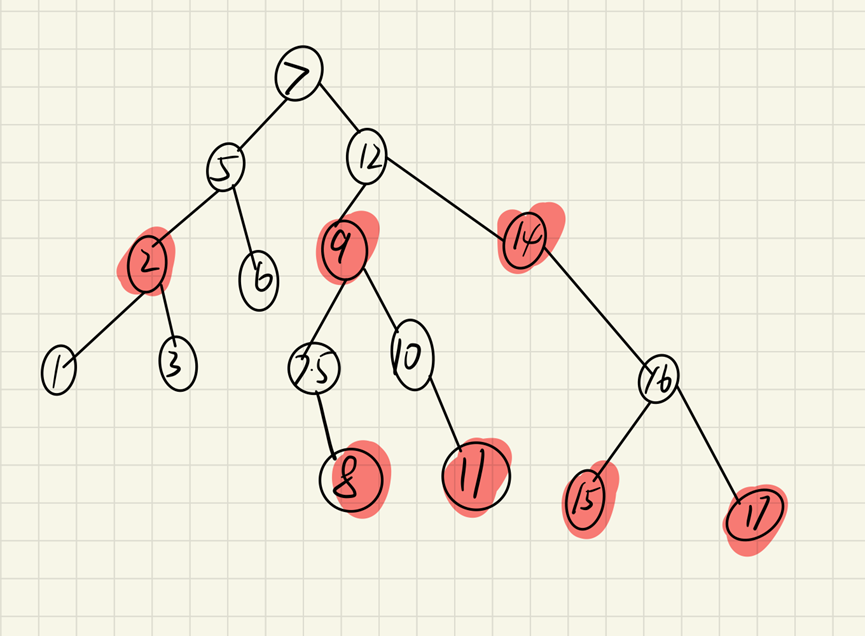
Left and right means that on the original balanced binary tree, a new node is inserted under the right subtree of the left subtree of the node, resulting in a height difference of 2 between the left and right subtrees of the node. As above, it is the left subtree "7" of the "11" node and the right subtree "9" of the "11" node,
Insertion of node "10" or "8" resulted in imbalance.
The left and right adjustment cannot be completed by one rotation like the left and left. We might as well try to rotate the "11" node from left to right like left to left. The result is as follows. The binary tree in the right figure is still unbalanced, and the right figure is the next step
Speaking of right and left, that is, left and right and left mirror each other, and left, left and right mirror each other.
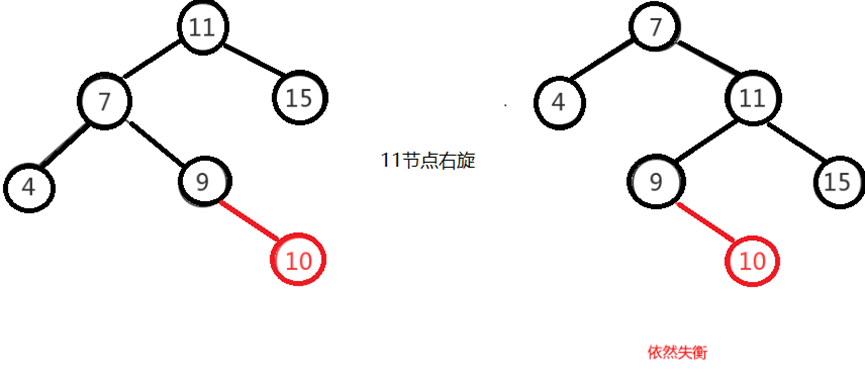
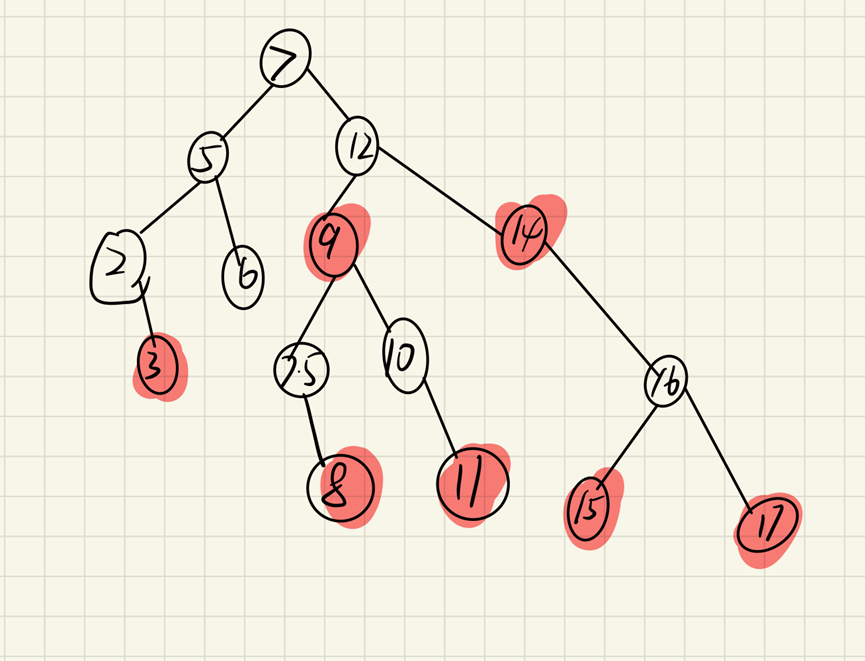
In this case, one rotation can not meet our conditions. The correct adjustment method is to rotate the left and right for the first time, adjust the left and right to left first, and then adjust the left and left, so as to balance the binary tree.
That is, first rotate the node "7" in the above figure to make the binary tree left, and then rotate the node "11" to the right. At this time, the binary tree adjustment is completed, as shown in the following figure:
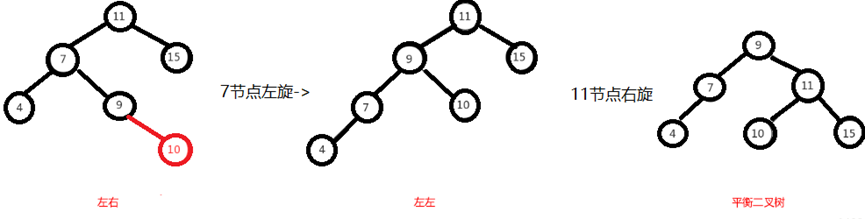
Right left
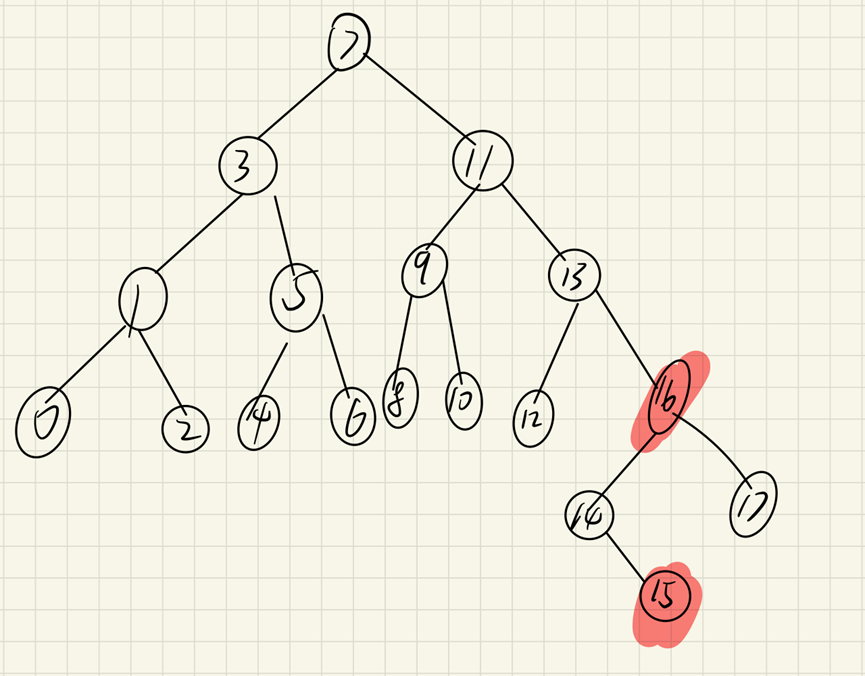
Right and left means that on the original balanced binary tree, a new node is inserted under the left subtree of the right subtree of the node, resulting in a height difference of 2 between the left and right subtrees of the node. As above, it is the right subtree "15" of the "11" node and the left subtree "13" of the "11" node,
Insertion of node "12" or "14" resulted in imbalance.
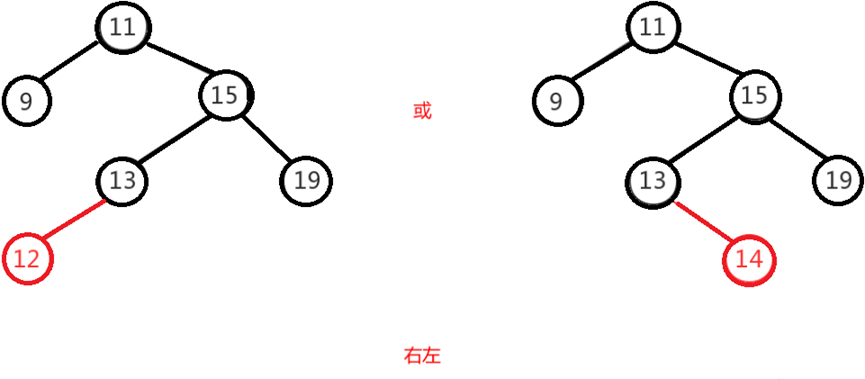
As mentioned earlier, the right, left, left and right are actually mirror images of each other, so the adjustment process is reversed. First rotate the node "15" to make the binary tree right, and then rotate the node "11" to the left. At this time, the binary tree adjustment is completed, as shown in the following figure:
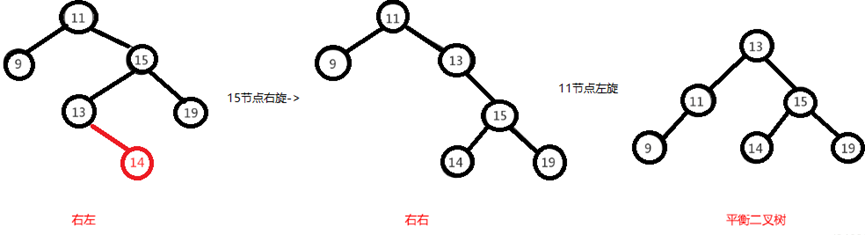
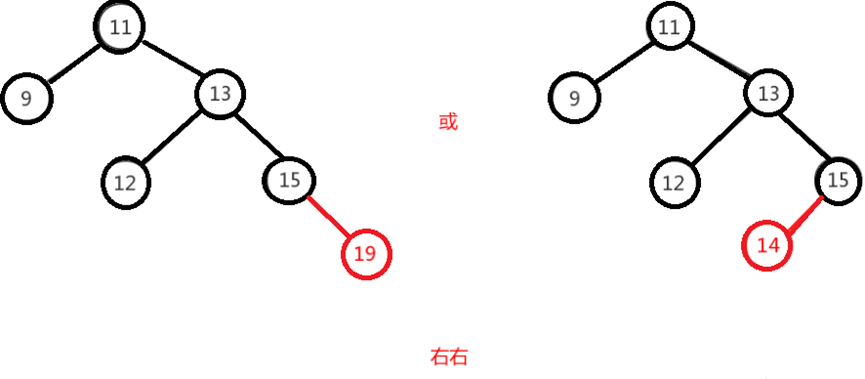
Right right
Right and right means that on the original balanced binary tree, a new node is inserted under the right subtree of the right subtree of the node, resulting in a height difference of 2 between the left and right subtrees of the node. As follows, the node is inserted into the right subtree "13" of node "11" and the left subtree "15"
"14" or "19" lead to imbalance.
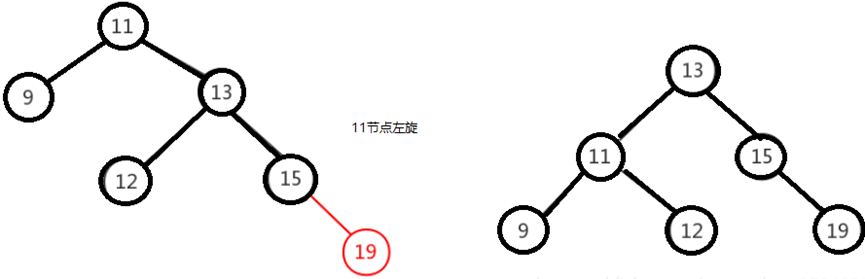
The balance can be adjusted only by turning the node left once. As shown in the figure below, turn the "11" node left.
234 tree
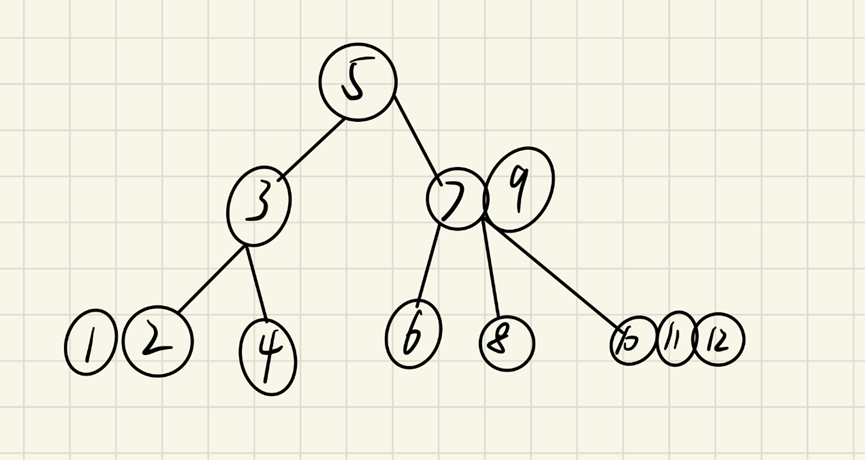
224 tree is a fourth-order B tree. It belongs to a multi-path lookup tree. Its structure has the following limitations
1. All leaf nodes have the same depth
2. The node can only be one of 2 nodes, 3 nodes and 4 nodes
3. The elements are always sorted, and the nature of binary search tree is maintained as a whole, that is, the parent node is greater than the left child node and less than the right child node; Moreover, when a node has multiple elements, each element must be greater than the element on its left and the element in its left subtree
The following figure shows a 234 tree
Due to the uncertainty of node elements, it is relatively difficult to implement 2-3-4# tree in most programming languages, because the operation on the tree involves a large number of special cases. The implementation of red black tree is simpler, so it can be used instead
Convert the above figure to a red black tree
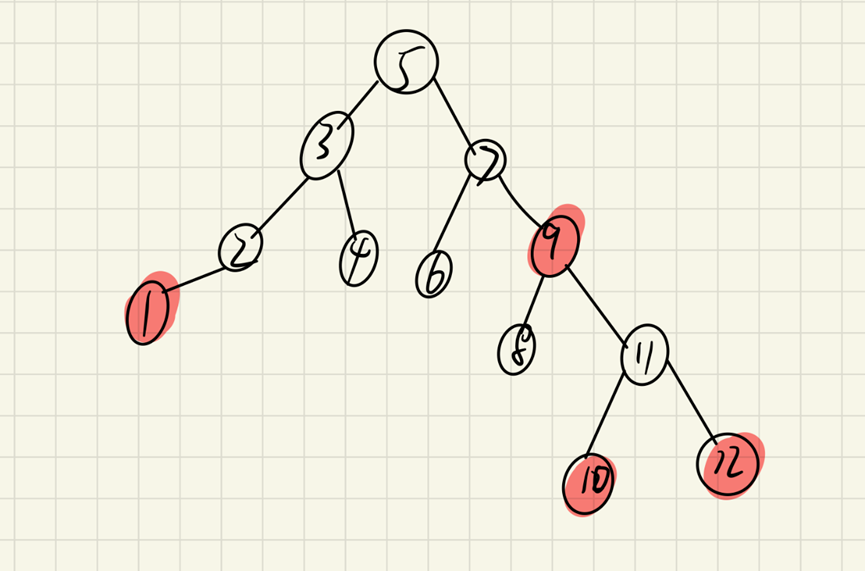
Converting 234 tree into red black tree is mainly the conversion of nodes
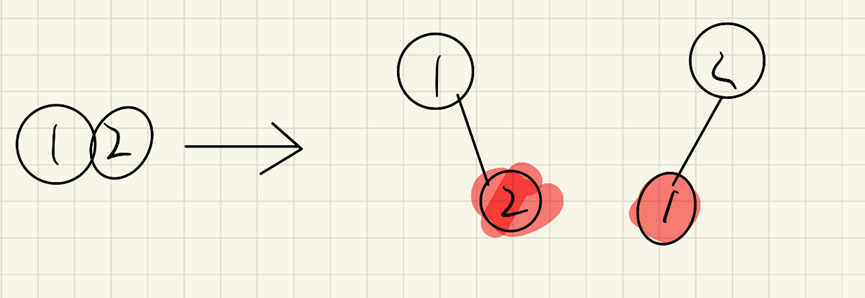
Second node:
Three nodes:
Four nodes:
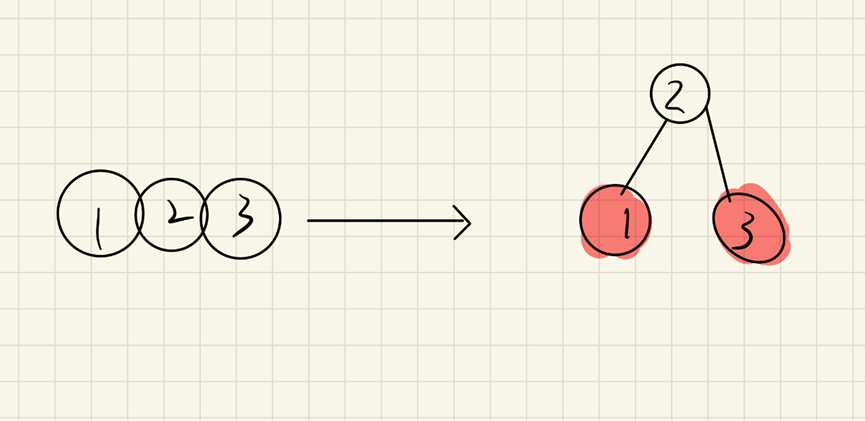
For this reason, I choose to add and delete the red black tree and 234 tree together.
Red black tree:
Red black tree is a specialized AVL tree (balanced binary tree), which maintains the balance of binary search tree through specific operations during insertion and deletion, so as to obtain high search performance.
Red black tree is a binary search tree with color attribute at each node, which is either red or black. [3] in addition to the mandatory General requirements for binary search trees, we have added the following additional requirements for any effective red black tree:
Nature 1 Nodes are red or black. [3]
Nature 2 The root node is black. [3]
Nature 3 All the leaves are black. (leaves are NIL nodes) [3]
Nature 4 The two child nodes of each red node are black. (there cannot be two consecutive red nodes on all paths from each leaf to the root)
Nature 5 All paths from any node to each leaf contain the same number of black nodes.
234 adding a tree
The first node does not need to be merged

2. Add a new node and merge directly with node 2
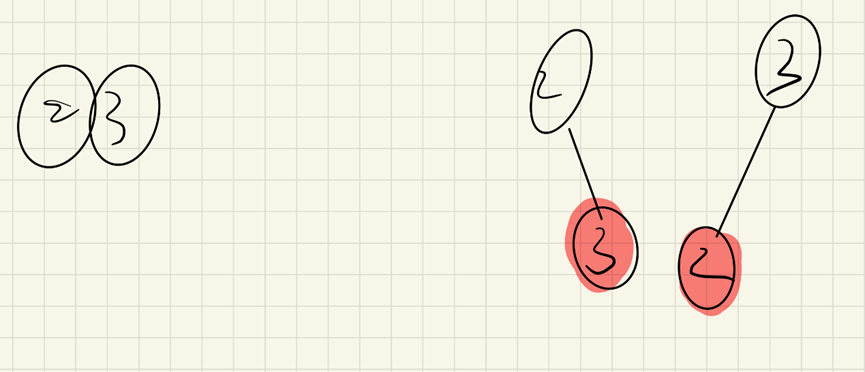
3 add a new node and merge with node 3
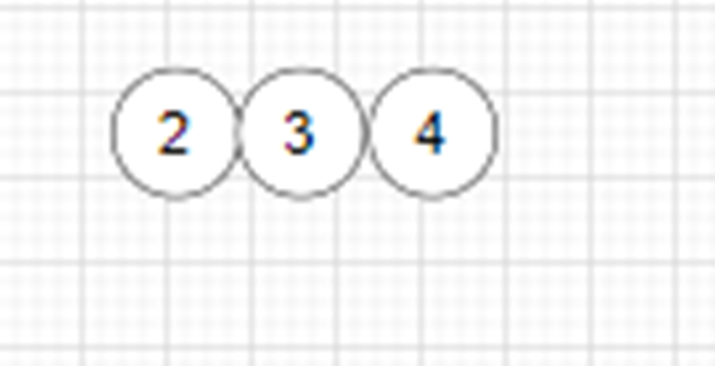
4. Add a new node and merge it with 4 nodes. At this time, it needs to be split
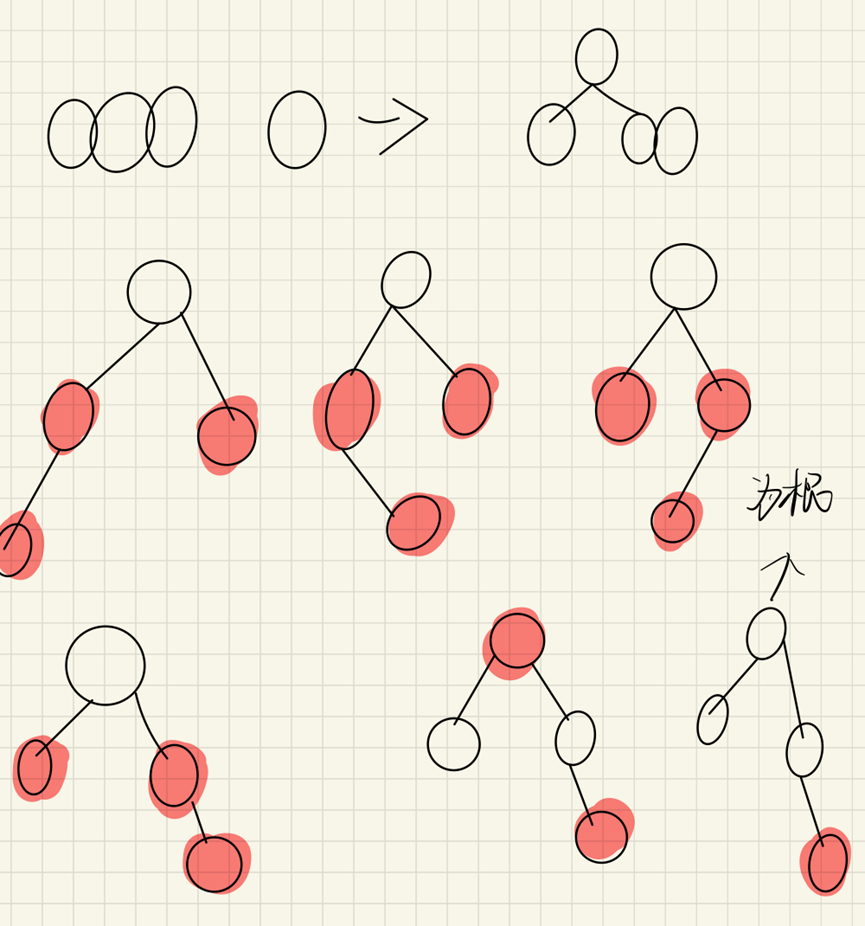
Code implementation:
Where 1 and 2 are added directly (addition of binary tree)
Color change after rotation in 3
4. You need to judge whether the parent node is root
The difference between 3 and 4 is to judge whether the inserted node has an uncle node.
Adding red black tree nodes
1. Query the insertion position first
2 encapsulate kv as a node object and insert it into the tree
3 balance of red and black trees (adjust rotation and color change)
Auxiliary methods:
private boolean colorOf(RBNode node){ return node == null ?BLACK :node.color; } private RBNode parentOf(RBNode node){ return node !=null ?node.parent:null; } private RBNode leftOf(RBNode node){ return node !=null?node.left:null; } private RBNode rightOf(RBNode node){ return node !=null ? node.right:null; } private void setColor(RBNode node,boolean color){ if(node!=null){ node.setColor(color); } }
New method:
public void put(K key,V value){ //Get root node RBNode t = this.root; if (t == null){ root = new RBNode(key,value==null?key:value,null); setColor(root,BLACK); return; } //Find where to insert int cmp; //Record the parent node of the lookup node RBNode parent; if (key == null){ throw new NullPointerException(); } do{ parent = t; cmp = key.compareTo((K)t.key); if(cmp<0){ t =t.left; }else if (cmp>0){ t=t .right; }else { t.setValue(value == null?key:value); return; } }while (t != null); //Indicates that the child node of the inserted parent is found RBNode e = new RBNode(key,value==null?key:value,parent); if (cmp<0){ parent.left = e; }else{ parent.right = e; } //Balance fixAfterPut(e); }
Treatment of red black tree balance
1. 2-3-4 tree: new element + 2 node consolidation (only 1 element in the node) = 3 nodes (2 elements in the node)
Red black tree: add a red node + black parent node = upper black and lower red (2 nodes) --------- do not adjust
2. 2-3-4 tree: new element + 3 node consolidation (2 elements in the node) = 4 nodes (3 elements in the node)
There are four small cases (left 3, right 3, and two left, middle and right do not need to be adjusted) --- left 3, right 3 need to be adjusted, and the other two do not need to be adjusted
Red black tree: new red node + upper black and lower red = after sorting, the middle node is black, and the nodes on both sides are red (3 nodes)
3. 2-3-4 tree: add an element + 4-node merge = the original 4-node split, the intermediate element is upgraded to the parent node, and the new element is merged with one of the remaining nodes
Red black tree: new red node + Black grandfather node. Both parent node and uncle node are red = grandpa node turns red, father and uncle turn black. If Grandpa is the root node, it turns black again
private void fixAfterPut(RBNode x) { setColor(x,RED); while (x!=null&&x!=root&&parentOf(x).color == RED){ //The parent node of x is the left child node of the grandfather node of x. there are four situations that need to be handled if (parentOf(x)==parentOf(parentOf(x)).left){ //The four conditions are divided into two according to whether there is an uncle node //Get the current node RBNode y = rightOf(parentOf(parentOf(x))); if (colorOf(y)==RED){ //Uncle node exists setColor(parentOf(x),BLACK); setColor(y,BLACK); setColor(parentOf(parentOf(x)),RED); //Recursive processing x = parentOf(parentOf(x)); }else { //2 if(x == rightOf(parentOf(x))){ //The inserted node is the right node of the parent node, and a left-hand operation needs to be performed according to the parent node x = parentOf(x); leftRotate(x); } setColor(parentOf(x),BLACK); setColor(parentOf(parentOf(x)),RED); rightRota(parentOf(parentOf(x))); } }else{ //Reverse the above operation //The four conditions are divided into two according to whether there is an uncle node //Get the current node RBNode y = leftOf(parentOf(parentOf(x))); if (colorOf(y)==RED){ //Uncle node exists setColor(parentOf(x),BLACK); setColor(y,BLACK); setColor(parentOf(parentOf(x)),RED); //Recursive processing x = parentOf(parentOf(x)); }else { //2 if (x == leftOf(parentOf(x))) { //The inserted node is the right node of the parent node, and a left-hand operation needs to be performed according to the parent node x = parentOf(x); rightRota(x); } setColor(parentOf(x), BLACK); setColor(parentOf(parentOf(x)), RED); leftRotate(parentOf(parentOf(x))); } } } //The root nodes are black setColor(root, BLACK); }
Red black tree deletion and 234 tree deletion
234 tree deletion can be converted into leaf node deletion. The deletion principle is to first see whether it can be merged with the following leaf nodes. If it can be merged, it can be merged and deleted directly
Delete operation:
Case 1 delete leaf node
(1) If it is red, delete it directly
(2) If it is black, the corresponding red black tree starts from the root node to all leaves. The number of black nodes on one path is 1 less than that on other paths, which does not meet the nature of the red black tree and requires color change and other adjustments
See the following (3) analysis of borrowing sibling node without child node
In case 2, the deleted node has a child node, and the child node must be red
In case 3, the node divided by has two child nodes. In this case, it is necessary to find a precursor node or a successor node to replace it. In addition, it is necessary to find an element to replace it. Finally, to maintain balance, that is, the operation of deleting a node is transformed into deleting a precursor or a successor node
There are only two cases of deleted predecessor nodes or successor nodes:
1. The deleted node is a leaf node
There are two cases
(1) The sibling node has child nodes (the node to be deleted in the figure is 4. In this paper, the replacement node is the successor node, and 8 is not the real sibling node of the successor node. First rotate 6 to the left)
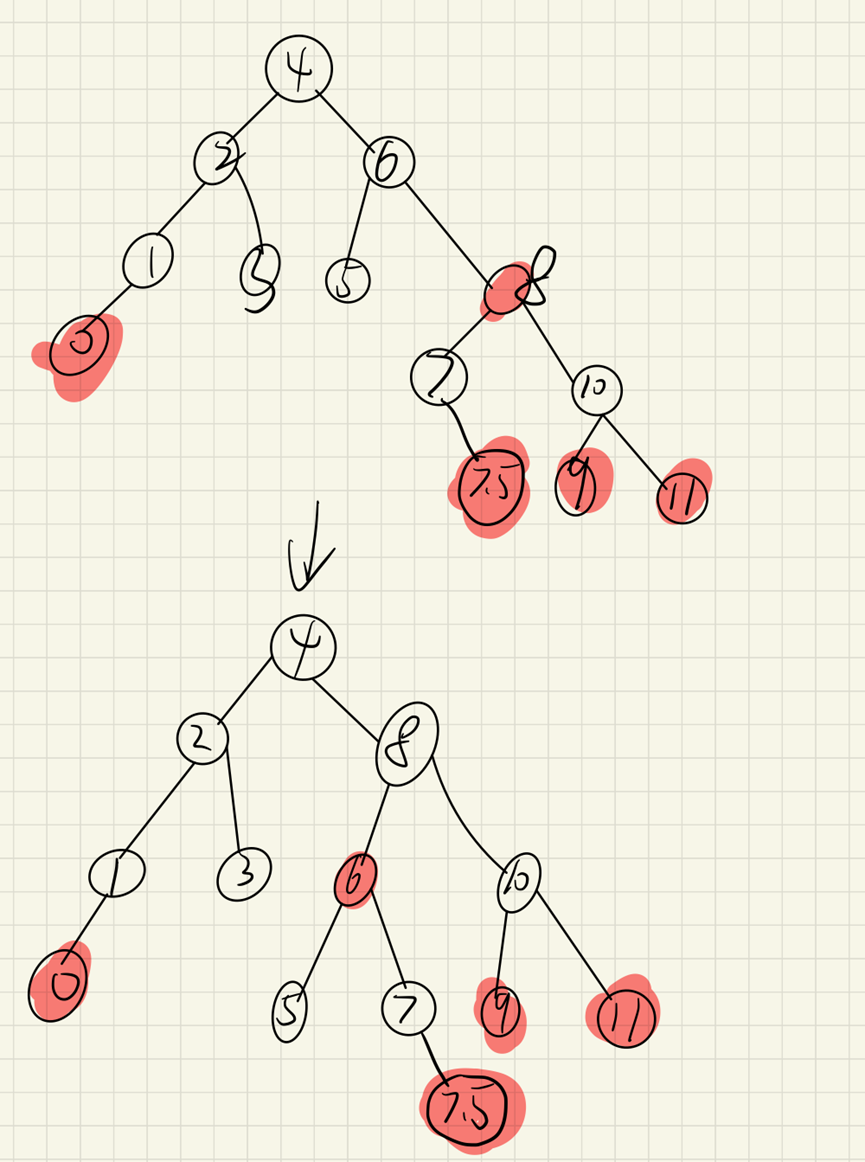
Turn the 6 nodes left and turn 5, 6, 7, 7.5 to change color
Finally, delete reference 1 from 5
(1) Borrowing sibling node has no child node
1. The parent node of the deleted node is red
At this time, the sibling node 3 of 1 has no child nodes. If you delete 1, the red black tree is not in the black balance, because there is less black node on the left side of the root node, so we can dye 3 red to make the local balance first and expand it to the overall balance
Because 2 and 3 cannot be red at the same time, and the black balance is not reached for node 5
Turn all 2 nodes black to achieve global balance
or
2. The parent node of the deleted node is black
0 is deleted
Since the sibling node has no child nodes, the sibling node will be dyed red. This method needs to have the idea of recursion. For the left local balance, the sibling node of the parent node of the deleted node will be dyed red. At this time, the left local balance of the root node
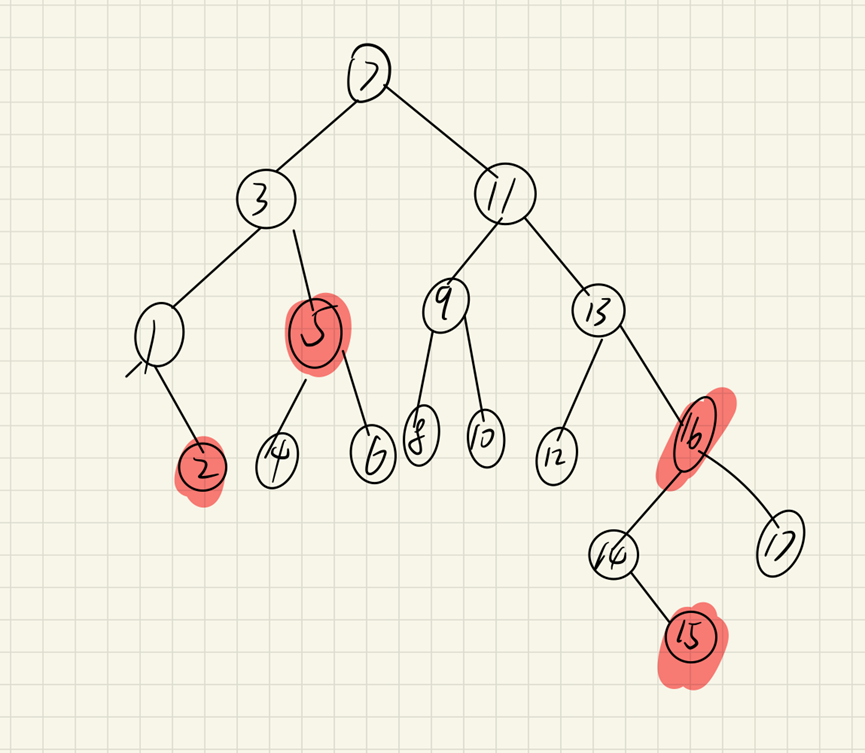
At this time, the left and right subtrees of 7 are unbalanced, and the brother node 11 of 3 cannot borrow, so dye the brother node of 3 red to achieve black balance. This method achieves the black red balance by recursively coloring the brother nodes
(I)
What if the sibling node is already red?
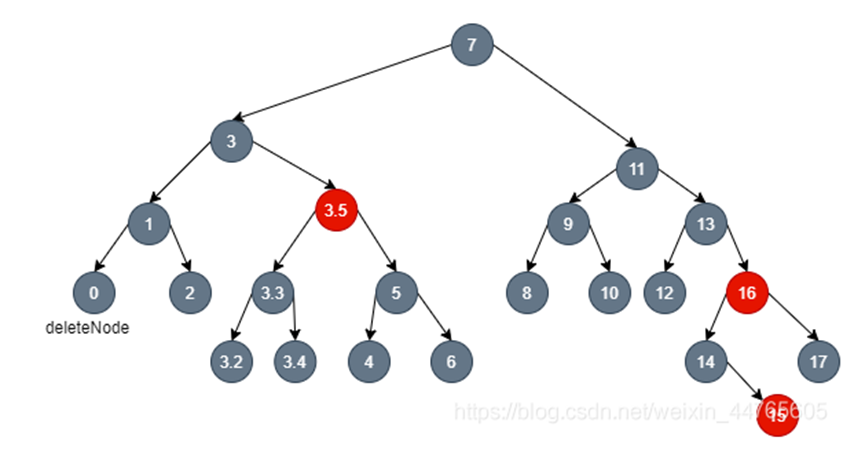
At this time, the sibling node is not a real sibling node
The true sibling node 3.3 is obtained by turning node 3 left and changing color
And change the color of brother nodes
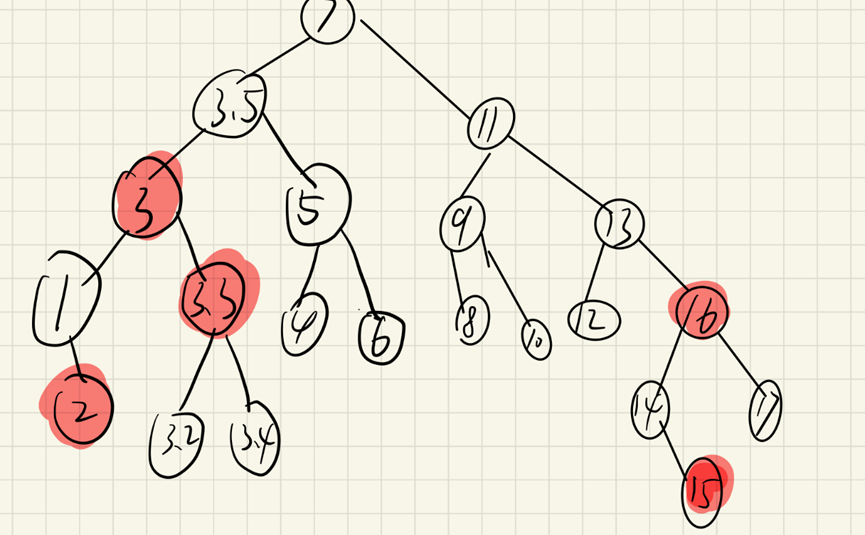
At this time, the black red balance is achieved by dyeing node 3 black.
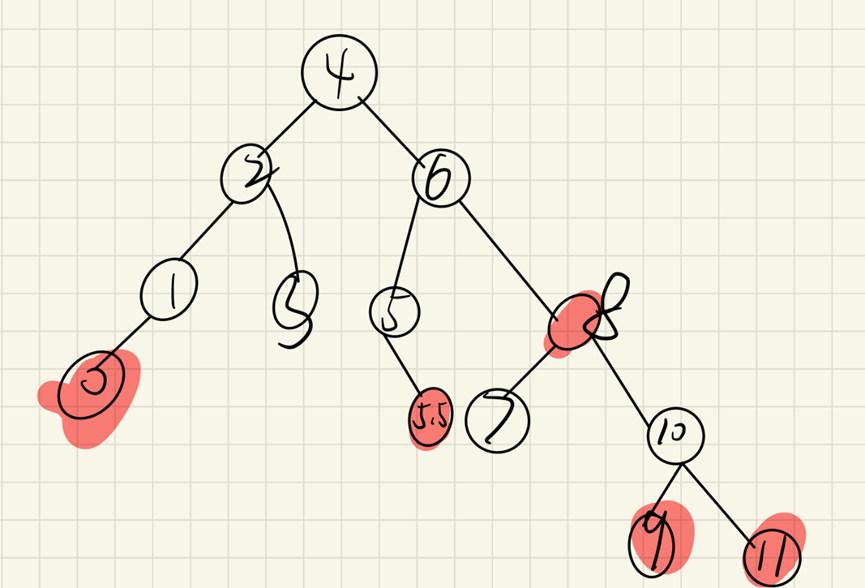
(2) If a sibling node that can be borrowed can be encountered when recursively maintaining local balance, as shown in the figure below
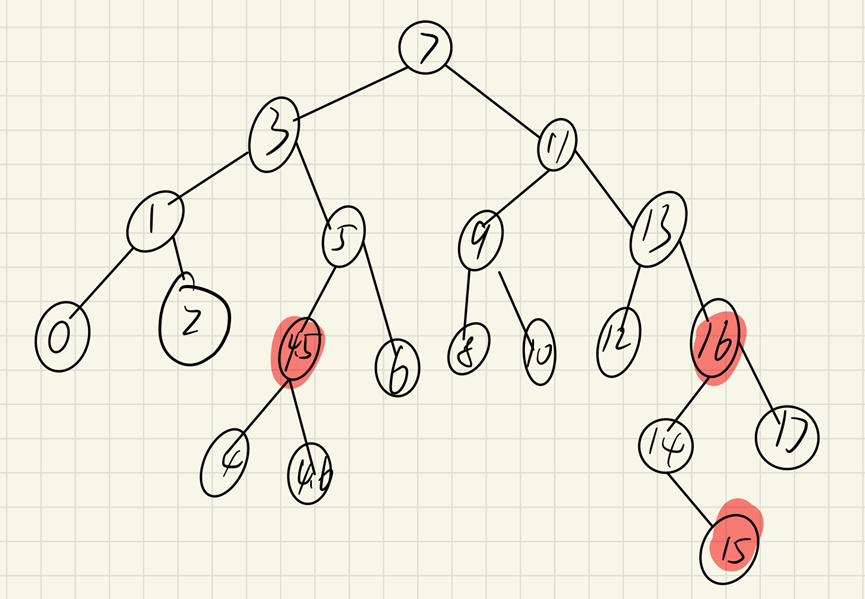
After deleting node 0 and changing the color of node 2, recursion. At this time, the brother node of 1 is 5. At this time, node 5 can be rotated to the right
At this time, the sibling node is 4.5. You can lend out 4, press down 3 nodes through the left rotation of 3 nodes and change the color of 5 nodes, so as to achieve global balance
2. The deleted node has only one child
This is case 2 deletion
Red black tree all codes:
package com.cn; public class RBTree<K extends Comparable<K>,V > { private static final boolean RED = false; private static final boolean BLACK= true; private RBNode root; public RBNode getRoot() { return root; } public void setRoot(RBNode root) { this.root = root; } /** * add to * Adding red black tree nodes * 1.Balance of common red and black trees * Query the insertion position first * Encapsulate kv as a node object and insert it into the tree * 2 Balance of red and black trees (adjust rotation and color change) * */ public void put(K key,V value){ //Get root node RBNode t = this.root; if (t == null){ root = new RBNode(key,value==null?key:value,null); setColor(root,BLACK); return; } //Find where to insert int cmp; //Record the parent node of the lookup node RBNode parent; if (key == null){ throw new NullPointerException(); } do{ parent = t; cmp = key.compareTo((K)t.key); if(cmp<0){ t =t.left; }else if (cmp>0){ t=t .right; }else { t.setValue(value == null?key:value); return; } }while (t != null); //Indicates that the child node of the inserted parent is found RBNode e = new RBNode(key,value==null?key:value,parent); if (cmp<0){ parent.left = e; }else{ parent.right = e; } //Balance fixAfterPut(e); } private boolean colorOf(RBNode node){ return node == null ?BLACK :node.color; } private RBNode parentOf(RBNode node){ return node !=null ?node.parent:null; } private RBNode leftOf(RBNode node){ return node !=null?node.left:null; } private RBNode rightOf(RBNode node){ return node !=null ? node.right:null; } private void setColor(RBNode node,boolean color){ if(node!=null){ node.setColor(color); } } /**Treatment of red black tree balance * * 1,2-3-4 Tree: new element + 2 nodes merge (only 1 element in the node) = 3 nodes (2 elements in the node) * * Red black tree: add a red node + black parent node = upper black and lower red (2 nodes) --------- do not adjust * * * * 2,2-3-4 Tree: new element + 3 node merging (2 elements in the node) = 4 nodes (3 elements in the node) * * There are four small cases (left 3, right 3, and two left, middle and right do not need to be adjusted) --- left 3, right 3 need to be adjusted, and the other two do not need to be adjusted * * Red black tree: new red node + upper black and lower red = after sorting, the middle node is black, and the nodes on both sides are red (3 nodes) * * * * 3,2-3-4 Tree: add a new element + 4 nodes merge = the original 4 nodes split, the intermediate element is upgraded to the parent node, and the new element is merged with one of the remaining nodes * * Red black tree: new red node + Black grandfather node. Both parent node and uncle node are red = grandpa node turns red, father and uncle turn black. If Grandpa is the root node, it turns black again * * * @param x */ private void fixAfterPut(RBNode x) { setColor(x,RED); while (x!=null&&x!=root&&parentOf(x).color == RED){ //The parent node of x is the left child node of the grandfather node of x. there are four situations that need to be handled if (parentOf(x)==parentOf(parentOf(x)).left){ //The four conditions are divided into two according to whether there is an uncle node //Get the current node RBNode y = rightOf(parentOf(parentOf(x))); if (colorOf(y)==RED){ //Uncle node exists setColor(parentOf(x),BLACK); setColor(y,BLACK); setColor(parentOf(parentOf(x)),RED); //Recursive processing x = parentOf(parentOf(x)); }else { //2 if(x == rightOf(parentOf(x))){ //The inserted node is the right node of the parent node, and a left-hand operation needs to be performed according to the parent node x = parentOf(x); leftRotate(x); } setColor(parentOf(x),BLACK); setColor(parentOf(parentOf(x)),RED); rightRota(parentOf(parentOf(x))); } }else{ //Reverse the above operation //The four conditions are divided into two according to whether there is an uncle node //Get the current node RBNode y = leftOf(parentOf(parentOf(x))); if (colorOf(y)==RED){ //Uncle node exists setColor(parentOf(x),BLACK); setColor(y,BLACK); setColor(parentOf(parentOf(x)),RED); //Recursive processing x = parentOf(parentOf(x)); }else { //2 if (x == leftOf(parentOf(x))) { //The inserted node is the right node of the parent node, and a left-hand operation needs to be performed according to the parent node x = parentOf(x); rightRota(x); } setColor(parentOf(x), BLACK); setColor(parentOf(parentOf(x)), RED); leftRotate(parentOf(parentOf(x))); } } } //The root nodes are black setColor(root, BLACK); } /** * Find the precursor node of node node * */ private RBNode predecessor(RBNode node){ if(node == null){ return null; } else if (node.left !=null){ RBNode p = node.left; while (p.right!=null){ p=p.right; } return p; } else { RBNode p = node.parent; RBNode ch = node; while (p!=null&&ch==p.left){ ch = p ; p = p.parent; } return p; } } /** * Find the successor node of node node * */ private RBNode successor(RBNode node){ if(node == null){ return null; } else if (node.right !=null){ RBNode p = node.right; while (p.left!=null){ p=p.left; } return p; } else { RBNode p = node.parent; RBNode ch = node; while (p!=null&&ch==p.right){ ch = p ; p = p.parent; } return p; } } public V remove(K key){ RBNode node = getNode(key); if (node ==null){ return null; } V oldValue = (V) node.value; deleteNode(node); return oldValue; } /** * Delete operation: * 1,Delete leaf node directly * 2,If the deleted node has a child node, replace it with a child node * 3,If the deleted node has 2 child nodes, you need to find a predecessor node or a successor node to replace it * @param node */ private void deleteNode(RBNode node) { //3 node has two children if (node.left!=null&&node.right!=null){ RBNode successor = successor(node); node.key= successor.key; node.value = successor.value; node = successor; } RBNode replacement = node.left!=null?node.left:node.right; //2 if (replacement !=null){ replacement.parent = node.parent; if(node.parent==null){ root = replacement; }else if (node==node.parent.left){ node.parent.left = replacement; }else { node.parent.right=replacement; } //node is free and waiting for garbage collection node.left = node.right=node.parent=null; //The balance needs to be adjusted after replacement if (node.color==BLACK){ //Need adjustment //This situation must be red (the replacement node must be red). At this time, as long as the color changes fixAfterRemove(node); } } else if (node.parent==null){ root = null; } //1 //Leaf nodes are deleted directly else{ //Adjust before deleting if (node.color==BLACK){ fixAfterRemove(node); } //Delete again if (node.parent!=null){ if (node == node.parent.left){ node.parent.left = null; } else if (node == node.parent.right){ node.parent.right =null; } //Bidirectional decoupling node.parent = null; } } } private void fixAfterRemove(RBNode x) { while (x!=root&&colorOf(x)==BLACK){ //x on the left if (x==leftOf(parentOf(x))){ RBNode rnode = rightOf(parentOf(x)); //Judge whether it is a real sibling node at this time if (colorOf(rnode)== RED){ setColor(rnode,BLACK); setColor(parentOf(x),RED); leftRotate(parentOf(x)); rnode = rightOf(parentOf(x)); } //Situation III if(colorOf(leftOf(rnode))==BLACK&&colorOf(rightOf(rnode))==BLACK){ setColor(rnode,RED); x=parentOf(x); } //Situation II else { //There are two cases //When the sibling node has no right child node if (colorOf(rightOf(rnode))==BLACK){ setColor(leftOf(rnode),BLACK); setColor(rnode,RED); rightRota(rnode); rnode = rightOf(parentOf(x)); } setColor(rnode,colorOf(parentOf(x))); setColor(parentOf(x),BLACK); setColor(rightOf(rnode),BLACK); leftRotate(parentOf(x)); x=root; } }//x on the right else { //Sibling node RBNode rnode = leftOf(parentOf(x)); //Judge whether the sibling node is a real sibling node at this time if(colorOf(rnode)==RED){ setColor(rnode,BLACK); setColor(parentOf(x),RED); rightRota(parentOf(x)); //Find the real sibling node rnode=leftOf(parentOf(x)); } //Situation three, ask brother to borrow, brother can't borrow if(colorOf(rightOf(rnode))==BLACK&&colorOf(leftOf(rnode))==BLACK){ //The situation is complicated. I won't write it for the time being setColor(rnode,RED); x=parentOf(x); } //Situation 2: borrow from brothers. Some brothers borrow else{ //There are two small cases: the sibling node is originally 3 nodes or 4 nodes if(colorOf(leftOf(rnode))==BLACK){ setColor(rightOf(rnode),BLACK); setColor(rnode,RED); leftRotate(rnode); rnode=leftOf(parentOf(x)); } setColor(rnode,colorOf(parentOf(x))); setColor(parentOf(x),BLACK); setColor(leftOf(rnode),BLACK); rightRota(parentOf(x)); x=root; } } } //When the alternative node is red, it will be dyed black directly setColor(x,BLACK); } private RBNode getNode(K key) { RBNode node = this.root; while (node!=null){ int cmp = key.compareTo((K) node.key); if (cmp<0){ node = node.left; }else if (cmp>0){ node = node.right; }else { return node; } } return null; } /** * Sinistral * p pr * / \ / \ * pl pr p rr * / \ / \ * rl rr pl rl */ public void leftRotate(RBNode p){ if(p!=null){ RBNode r = p.right; //PR RL becomes p-rl p.right = r.left; if (r.left!=null){ r.left.parent = p; } //Determine whether p has a parent node r.parent = p.parent; if (p.parent == null){ root = r; }else if (p.parent.left ==p){ p.parent.left = r; }else { p.parent.right = r; } //Finally, set p as the left child node of r r.left = p; p.parent = r; } } /** * Dextral * @param p */ public void rightRota(RBNode p){ if(p!=null){ RBNode r = p.left; //PR RL becomes p-rl p.left = r.right; if (r.right!=null){ r.left.parent = p; } //Determine whether p has a parent node r.parent = p.parent; if (p.parent == null){ root = r; }else if (p.parent.left ==p){ p.parent.left = r; }else { p.parent.right = r; } //Finally, set p as the left child node of r r.right = p; p.parent = r; } } //Node type static class RBNode<K extends Comparable<K>,V>{ private RBNode parent; private RBNode right; private RBNode left; private boolean color; private K key; private V value; public RBNode(RBNode parent, RBNode right, RBNode left, boolean color, K key, V value) { this.parent = parent; this.right = right; this.left = left; this.color = color; this.key = key; this.value = value; } public RBNode(K key, V value,RBNode parent) { this.parent = parent; this.key = key; this.value = value; } public RBNode() { } public RBNode getParent() { return parent; } public void setParent(RBNode parent) { this.parent = parent; } public RBNode getRight() { return right; } public void setRight(RBNode right) { this.right = right; } public RBNode getLeft() { return left; } public void setLeft(RBNode left) { this.left = left; } public boolean isColor() { return color; } public void setColor(boolean color) { this.color = color; } public K getKey() { return key; } public void setKey(K key) { this.key = key; } public V getValue() { return value; } public void setValue(V value) { this.value = value; } } }
I suggest you take a look at this (25 messages) experience of learning red black tree_ Lazy Jie's blog - CSDN blog_ How to learn red black tree