Red black tree
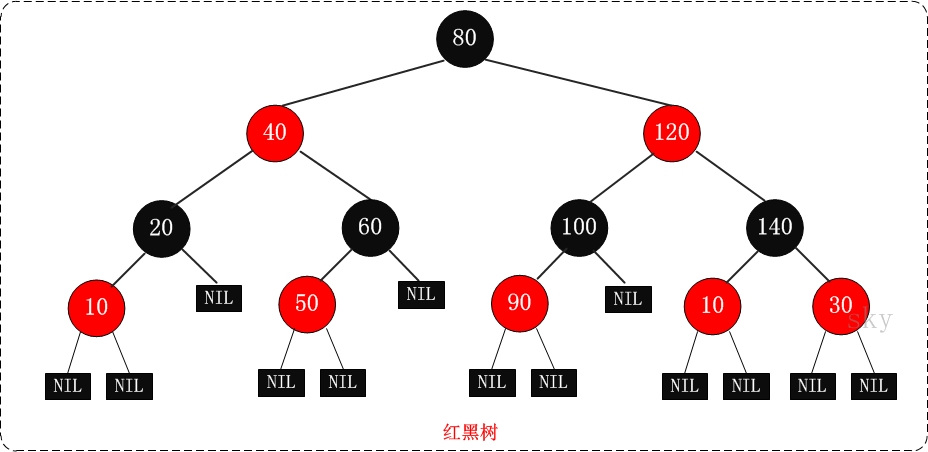
Red black tree rule features:
- Nodes are red or black;
- The root node must be black;
- All leaf nodes are black and null;
- The two child nodes connecting the red node are black (no adjacent red nodes appear in the red black tree);
- Starting from any node, the path to each leaf node contains the same number of black nodes;
- The nodes newly added to the red black tree are red nodes;
The basic operations of red black tree are add, delete and rotate. After adding or deleting the red black tree, the rotation method will be used.
The search, addition and deletion of red black trees are all O(logn)
Common uses of red black tree:
1. Application of Linux in non real time task scheduling
After 2.6.24, the stable kernel version of Linux uses the new scheduler CFS. All non real-time runnable processes are hung on a red black tree with the virtual running time as the key value, so as to schedule all tasks more fairly and efficiently. CFS discards the active /expired array and dynamic calculation priority, no longer tracks the sleep time of the task and distinguishes whether the task is interactive or not, and uses the red black tree based on the time calculation key value to select the next task in the scheduling, and determines the scheduling task priority according to the CPU time occupied by all tasks. [3]
2. Application of Linux in virtual memory
The 32-bit Linux kernel virtual address space is divided into 0-3G as user space and 3-4G as kernel space, so each process can use 4GB of virtual space. At the same time, Linux defines virtual storage areas (Vmas) to better represent the virtual space used by processes. Each VMA is a continuous virtual space of a process, in which the units have the same characteristics. All virtual areas are sorted by address and linked into a linked list by pointers. When a page missing interrupt occurs, searching VMA to the specified area requires frequent operations. Therefore, red black tree is selected to reduce the search time. [3]
3. Application of detection tree on balance
Red black tree is a kind of self Balanced binary search tree , each node is "colored" as red or black, and the color of these nodes is used to detect the balance of the tree. Red black tree as embedded database For SQLite database, red black tree can be used to optimize the index mechanism. [6]
4. Collection framework of Java (HashMap, TreeMap, TreeSet)
5. Timer management of nginx
The red black tree is used to manage timers. Because the red black tree is orderly, the timer with the smallest distance from the current can be quickly obtained
6. The implementation of IO multiplexing epoll adopts red black tree organization to manage sockfd to support rapid addition, deletion, modification and query
7. In C + + STL, map and set are implemented by red black tree
The following is the specific implementation of red black tree:
1. Basic definition:
public class RBTree<T extends Comparable<T>> {
private RBTNode<T> mRoot; // Root node
private static final boolean RED = false;
private static final boolean BLACK = true;
public class RBTNode<T extends Comparable<T>> {
boolean color; // colour
T key; // Keywords (key values)
RBTNode<T> left; // Left child
RBTNode<T> right; // Right child
RBTNode<T> parent; // Parent node
public RBTNode(T key, boolean color, RBTNode<T> parent, RBTNode<T> left, RBTNode<T> right) {
this.key = key;
this.color = color;
this.parent = parent;
this.left = left;
this.right = right;
}
}
}
...
2. Left hand rotation:
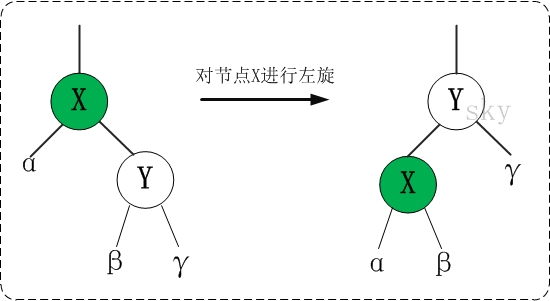
/*
* Rotate the node (x) of the red black tree to the left
*
* Left hand rotation diagram (left hand rotation of node x):
* px px
* / /
* x y
* / \ --(Left handed) -. / \#
* lx y x ry
* / \ / \
* ly ry lx ly
*
*
*/
private void leftRotate(RBTNode<T> x) {
// Set the right child of x to y
RBTNode<T> y = x.right;
// Set "left child of y" to "right child of x";
// If y's left child is not empty, set "x" to "Y's left child's father"
x.right = y.left;
if (y.left != null)
y.left.parent = x;
// Set "father of x" to "father of y"
y.parent = x.parent;
if (x.parent == null) {
this.mRoot = y; // If the parent of x is an empty node, set y as the root node
} else {
if (x.parent.left == x)
x.parent.left = y; // If x is the left child of its parent node, set y as the left child of X's parent node
else
x.parent.right = y; // If x is the left child of its parent node, set y as the left child of X's parent node
}
// Set "x" to "y's left child"
y.left = x;
// Set "parent of x" to "y"
x.parent = y;
}
3. Right hand rotation:
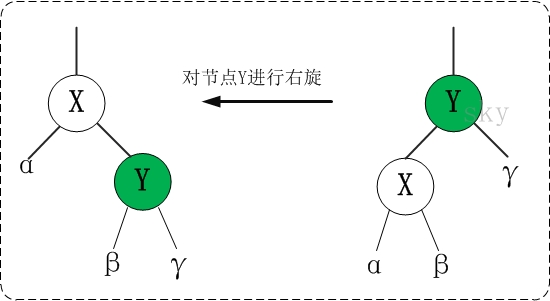
/*
* Rotate the node (y) of the red black tree to the right
*
* Schematic diagram of right rotation (left rotation of node y):
* py py
* / /
* y x
* / \ --(Right handed) -. / \#
* x ry lx y
* / \ / \ #
* lx rx rx ry
*
*/
private void rightRotate(RBTNode<T> y) {
// Set x to be the left child of the current node.
RBTNode<T> x = y.left;
// Set "right child of x" to "left child of y";
// If "x's right child" is not empty, set "y" to "x's right child's father"
y.left = x.right;
if (x.right != null)
x.right.parent = y;
// Set "father of y" to "father of x"
x.parent = y.parent;
if (y.parent == null) {
this.mRoot = x; // If "y's father" is an empty node, set x as the root node
} else {
if (y == y.parent.right)
y.parent.right = x; // If y is the right child of its parent node, set x to "the right child of Y's parent node"
else
y.parent.left = x; // (y is the left child of its parent node) set x as "the left child of x's parent node"
}
// Set "y" to "right child of x"
x.right = y;
// Set "parent node of y" to "x"
y.parent = x;
}
4. Add
What steps should be taken to insert a node into the red black tree? Firstly, the red black tree is regarded as a binary search tree, and the nodes are inserted; Then, color the node red; Finally, the tree is modified by a series of operations such as "rotation and recolor" to make it a red black tree again. Detailed description is as follows:
Step 1: treat the red black tree as a binary lookup tree and insert the node.
The red black tree itself is a binary lookup tree. After inserting nodes, the tree is still a binary lookup tree. That means that the key values of the tree are still ordered. In addition, whether it is left-handed or right-handed, if the tree is a binary lookup tree before rotation, it must still be a binary lookup tree after rotation. This means that any rotation and recolor operation will not change the fact that it is still a binary lookup tree.
ok Next, we'll try our best to rotate and re color the tree to make it a red black tree again!
Step 2: shade the inserted node as "red".
Why is it colored red instead of black? Why? Before answering, we need to review the characteristics of red black tree:
(1) Each node is either black or red.
(2) The root node is black.
(3) Each leaf node is black. [Note: leaf nodes here refer to empty leaf nodes!]
(4) If a node is red, its child nodes must be black.
(5) All paths from a node to its descendants contain the same number of black nodes.
Coloring the inserted node red will not violate the "property (5)"! The less we violate a feature, the fewer situations we need to deal with. Next, we should strive to make the tree meet other properties; If satisfied, it will be a red and black tree again. o(∩) o... Ha ha
Step 3: make it a red black tree again through a series of operations such as rotation or coloring.
In the second step, after shading the inserted node to red, the property (5) is not violated. What characteristics does it violate?
For "characteristic (1)", it is obvious that it will not be violated. Because we have painted it red.
For "characteristic (2)", it is obvious that it will not be violated. In the first step, we treat the red black tree as a binary lookup tree, and then perform the insertion operation. According to the characteristics of binary lookup number, the insertion operation will not change the root node. Therefore, the root node is still black.
For "characteristic (3)", it is obvious that it will not be violated. Leaf nodes here refer to empty leaf nodes. Inserting non empty nodes will not affect them.
For "feature (4)", it may be violated!
Next, find a way to "meet feature (4)" and reconstruct the tree into a red black tree.
/*
* Insert the node into the red black tree
*
* Parameter Description:
* node The inserted node / / corresponds to the node in introduction to algorithms
*/
private void insert(RBTNode<T> node) {
int cmp;
RBTNode<T> y = null;
RBTNode<T> x = this.mRoot;
// 1. Treat the red black tree as a binary lookup tree and add nodes to the binary lookup tree.
while (x != null) {
y = x;
cmp = node.key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else
x = x.right;
}
node.parent = y;
if (y!=null) {
cmp = node.key.compareTo(y.key);
if (cmp < 0)
y.left = node;
else
y.right = node;
} else {
this.mRoot = node;
}
// 2. Set the color of the node to red
node.color = RED;
// 3. Revise it to a binary search tree
insertFixUp(node);
}
/*
* Create a new node (key) and insert it into the red black tree
*
* Parameter Description:
* key Insert key value of node
*/
public void insert(T key) {
RBTNode<T> node=new RBTNode<T>(key,BLACK,null,null,null);
// If the new node fails, return.
if (node != null)
insert(node);
}
Internal interface – the function of insert(node) is to insert the "node" node into the red black tree.
External interface – the function of insert(key) is to add "key" to the red black tree.
Implementation code for adding correction operation:
/*
* Red black tree insertion correction function
*
* After inserting a node into the red black tree (out of balance), call this function again;
* The aim is to reshape it into a red black tree.
*
* Parameter Description:
* node The inserted node / / corresponds to z in introduction to algorithms
*/
private void insertFixUp(RBTNode<T> node) {
RBTNode<T> parent, gparent;
// If "the parent node exists and the color of the parent node is red"
while (((parent = parentOf(node))!=null) && isRed(parent)) {
gparent = parentOf(parent);
//If "parent node" is "left child of grandfather node"
if (parent == gparent.left) {
// Case 1 condition: the uncle node is red
RBTNode<T> uncle = gparent.right;
if ((uncle!=null) && isRed(uncle)) {
setBlack(uncle);
setBlack(parent);
setRed(gparent);
node = gparent;
continue;
}
// Case 2 condition: the uncle is black and the current node is the right child
if (parent.right == node) {
RBTNode<T> tmp;
leftRotate(parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 3 condition: the uncle is black and the current node is the left child.
setBlack(parent);
setRed(gparent);
rightRotate(gparent);
} else { //If "parent node of z" is "right child of grandfather node of z"
// Case 1 condition: the uncle node is red
RBTNode<T> uncle = gparent.left;
if ((uncle!=null) && isRed(uncle)) {
setBlack(uncle);
setBlack(parent);
setRed(gparent);
node = gparent;
continue;
}
// Case 2 condition: the uncle is black and the current node is the left child
if (parent.left == node) {
RBTNode<T> tmp;
rightRotate(parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 3 condition: the uncle is black and the current node is the right child.
setBlack(parent);
setRed(gparent);
leftRotate(gparent);
}
}
// Set the root node to black
setBlack(this.mRoot);
}
5. Delete
Delete a node in the red black tree. The operations to be performed are as follows: first, treat the red black tree as a binary lookup tree and delete the node from the binary lookup tree; Then, the tree is modified through a series of "rotation and recolor" to make it a red black tree again. Detailed description is as follows:
Step 1: treat the red black tree as a binary lookup tree and delete the node.
This is the same as "deleting nodes in a regular binary lookup tree". There are three situations:
① The deleted node has no son, that is, it is a leaf node. Then, delete the node directly.
② The deleted node has only one son. Then, delete the node directly and replace its position with the only child node of the node.
③ The deleted node has two sons. Then, first find its successor nodes; Then copy "the content of its successor node" to "the content of this node"; After that, delete its successor node. Here, the successor node is equivalent to a substitute. After copying the contents of the successor node to the deleted node, the successor node is deleted. In this way, the problem is cleverly transformed into the case of "deleting successor nodes". Next, consider the successor nodes. When the deleted node has two non empty child nodes, its successor nodes cannot be Gemini non empty. Since the "successor node of" cannot have both Gemini and non empty, it means that the "successor node of this node" either has no son or only one son. If there is no son, it shall be handled according to "situation ①"; If there is only one son, it shall be handled according to "situation ②".
Step 2: modify the tree through a series of "rotation and recolor" to make it a red black tree again.
Because deleting a node in step 1 may violate the characteristics of the red black tree. Therefore, you need to modify the tree through "rotation and recolor" to make it a red black tree again.
/*
* Delete the node and return the deleted node
*
* Parameter Description:
* node Deleted node
*/
private void remove(RBTNode<T> node) {
RBTNode<T> child, parent;
boolean color;
// The "left and right children are not empty" of the deleted node.
if ( (node.left!=null) && (node.right!=null) ) {
// The successor node of the deleted node. (called "replace node")
// Use it to replace the position of "deleted node", and then remove the "deleted node".
RBTNode<T> replace = node;
// Get successor node
replace = replace.right;
while (replace.left != null)
replace = replace.left;
// "Node node" is not a root node (only the root node does not have a parent node)
if (parentOf(node)!=null) {
if (parentOf(node).left == node)
parentOf(node).left = replace;
else
parentOf(node).right = replace;
} else {
// "Node node" is the root node. Update the root node.
this.mRoot = replace;
}
// Child is the right child of "replace node" and the node that needs to be "adjusted".
// There must be no left child in "replace node"! Because it is a successor node.
child = replace.right;
parent = parentOf(replace);
// Saves the color of the replace node
color = colorOf(replace);
// The deleted node is the parent node of its successor node
if (parent == node) {
parent = replace;
} else {
// child is not empty
if (child!=null)
setParent(child, parent);
parent.left = child;
replace.right = node.right;
setParent(node.right, replace);
}
replace.parent = node.parent;
replace.color = node.color;
replace.left = node.left;
node.left.parent = replace;
if (color == BLACK)
removeFixUp(child, parent);
node = null;
return ;
}
if (node.left !=null) {
child = node.left;
} else {
child = node.right;
}
parent = node.parent;
// Saves the color of the replace node
color = node.color;
if (child!=null)
child.parent = parent;
// 'node node' is not a root node
if (parent!=null) {
if (parent.left == node)
parent.left = child;
else
parent.right = child;
} else {
this.mRoot = child;
}
if (color == BLACK)
removeFixUp(child, parent);
node = null;
}
/*
* Delete node (z) and return the deleted node
*
* Parameter Description:
* tree Root node of red black tree
* z Deleted node
*/
public void remove(T key) {
RBTNode<T> node;
if ((node = search(mRoot, key)) != null)
remove(node);
}
Internal interface – the function of remove(node) is to insert the "node" node into the red black tree.
External interface – remove(key) deletes the node whose key value is key in the red black tree.
Implementation code of delete correction operation (Java language)
/*
* Red black tree deletion correction function
*
* After deleting the inserted node from the red black tree (the red black tree is out of balance), call this function again;
* The aim is to reshape it into a red black tree.
*
* Parameter Description:
* node Nodes to be corrected
*/
private void removeFixUp(RBTNode<T> node, RBTNode<T> parent) {
RBTNode<T> other;
while ((node==null || isBlack(node)) && (node != this.mRoot)) {
if (parent.left == node) {
other = parent.right;
if (isRed(other)) {
// Case 1: x's brother w is red
setBlack(other);
setRed(parent);
leftRotate(parent);
other = parent.right;
}
if ((other.left==null || isBlack(other.left)) &&
(other.right==null || isBlack(other.right))) {
// Case 2: x's brother w is black, and w's two children are also black
setRed(other);
node = parent;
parent = parentOf(node);
} else {
if (other.right==null || isBlack(other.right)) {
// Case 3: x's brother w is black, and w's left child is red and right child is black.
setBlack(other.left);
setRed(other);
rightRotate(other);
other = parent.right;
}
// Case 4: x's brother w is black; And w's right child is red, and the left child is of any color.
setColor(other, colorOf(parent));
setBlack(parent);
setBlack(other.right);
leftRotate(parent);
node = this.mRoot;
break;
}
} else {
other = parent.left;
if (isRed(other)) {
// Case 1: x's brother w is red
setBlack(other);
setRed(parent);
rightRotate(parent);
other = parent.left;
}
if ((other.left==null || isBlack(other.left)) &&
(other.right==null || isBlack(other.right))) {
// Case 2: x's brother w is black, and w's two children are also black
setRed(other);
node = parent;
parent = parentOf(node);
} else {
if (other.left==null || isBlack(other.left)) {
// Case 3: x's brother w is black, and w's left child is red and right child is black.
setBlack(other.right);
setRed(other);
leftRotate(other);
other = parent.left;
}
// Case 4: x's brother w is black; And w's right child is red, and the left child is of any color.
setColor(other, colorOf(parent));
setBlack(parent);
setBlack(other.left);
rightRotate(parent);
node = this.mRoot;
break;
}
}
}
if (node!=null)
setBlack(node);
}
6. Detailed code:
public class RBTree<T extends Comparable<T>> {
private RBTNode<T> mRoot; // Root node
private static final boolean RED = false;
private static final boolean BLACK = true;
public class RBTNode<T extends Comparable<T>> {
boolean color; // colour
T key; // Keywords (key values)
RBTNode<T> left; // Left child
RBTNode<T> right; // Right child
RBTNode<T> parent; // Parent node
public RBTNode(T key, boolean color, RBTNode<T> parent, RBTNode<T> left, RBTNode<T> right) {
this.key = key;
this.color = color;
this.parent = parent;
this.left = left;
this.right = right;
}
public T getKey() {
return key;
}
public String toString() {
return ""+key+(this.color==RED?"(R)":"B");
}
}
public RBTree() {
mRoot=null;
}
private RBTNode<T> parentOf(RBTNode<T> node) {
return node!=null ? node.parent : null;
}
private boolean colorOf(RBTNode<T> node) {
return node!=null ? node.color : BLACK;
}
private boolean isRed(RBTNode<T> node) {
return ((node!=null)&&(node.color==RED)) ? true : false;
}
private boolean isBlack(RBTNode<T> node) {
return !isRed(node);
}
private void setBlack(RBTNode<T> node) {
if (node!=null)
node.color = BLACK;
}
private void setRed(RBTNode<T> node) {
if (node!=null)
node.color = RED;
}
private void setParent(RBTNode<T> node, RBTNode<T> parent) {
if (node!=null)
node.parent = parent;
}
private void setColor(RBTNode<T> node, boolean color) {
if (node!=null)
node.color = color;
}
/*
* Pre order traversal of "red black tree"
*/
private void preOrder(RBTNode<T> tree) {
if(tree != null) {
System.out.print(tree.key+" ");
preOrder(tree.left);
preOrder(tree.right);
}
}
public void preOrder() {
preOrder(mRoot);
}
/*
* Middle order traversal of "red black tree"
*/
private void inOrder(RBTNode<T> tree) {
if(tree != null) {
inOrder(tree.left);
System.out.print(tree.key+" ");
inOrder(tree.right);
}
}
public void inOrder() {
inOrder(mRoot);
}
/*
* Traversing the "red black tree" in sequence
*/
private void postOrder(RBTNode<T> tree) {
if(tree != null)
{
postOrder(tree.left);
postOrder(tree.right);
System.out.print(tree.key+" ");
}
}
public void postOrder() {
postOrder(mRoot);
}
/*
* (Recursive implementation) find the node with key value in "red black tree x"
*/
private RBTNode<T> search(RBTNode<T> x, T key) {
if (x==null)
return x;
int cmp = key.compareTo(x.key);
if (cmp < 0)
return search(x.left, key);
else if (cmp > 0)
return search(x.right, key);
else
return x;
}
public RBTNode<T> search(T key) {
return search(mRoot, key);
}
/*
* (Non recursive implementation) find the node with key value in "red black tree x"
*/
private RBTNode<T> iterativeSearch(RBTNode<T> x, T key) {
while (x!=null) {
int cmp = key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else if (cmp > 0)
x = x.right;
else
return x;
}
return x;
}
public RBTNode<T> iterativeSearch(T key) {
return iterativeSearch(mRoot, key);
}
/*
* Find minimum node: returns the minimum node of the red black tree whose tree is the root node.
*/
private RBTNode<T> minimum(RBTNode<T> tree) {
if (tree == null)
return null;
while(tree.left != null)
tree = tree.left;
return tree;
}
public T minimum() {
RBTNode<T> p = minimum(mRoot);
if (p != null)
return p.key;
return null;
}
/*
* Find maximum node: returns the maximum node of the red black tree whose tree is the root node.
*/
private RBTNode<T> maximum(RBTNode<T> tree) {
if (tree == null)
return null;
while(tree.right != null)
tree = tree.right;
return tree;
}
public T maximum() {
RBTNode<T> p = maximum(mRoot);
if (p != null)
return p.key;
return null;
}
/*
* Find the successor node of node (x). That is, find the "minimum node" where the data value in the red black tree is greater than this node.
*/
public RBTNode<T> successor(RBTNode<T> x) {
// If x has a right child, then "the successor node of X" is "the smallest node of the subtree with its right child as the root".
if (x.right != null)
return minimum(x.right);
// If x there is no right child. Then x there are two possibilities:
// (01) if x is "a left child", then "the successor node of X" is "its parent node".
// (02) if x is "a right child", find "the lowest parent node of X, and the parent node must have a left child". The "lowest parent node" found is "the successor node of X".
RBTNode<T> y = x.parent;
while ((y!=null) && (x==y.right)) {
x = y;
y = y.parent;
}
return y;
}
/*
* Find the precursor node of node (x). That is, find the "maximum node" where the data value in the red black tree is less than this node.
*/
public RBTNode<T> predecessor(RBTNode<T> x) {
// If x has a left child, the "precursor node of X" is "the largest node of the subtree with its left child as the root".
if (x.left != null)
return maximum(x.left);
// If x there is no left child. Then x there are two possibilities:
// (01) if x is "a right child", then "the precursor node of X" is "its parent node".
// (01) if x is "a left child", find "the lowest parent node of X, and the parent node must have a right child". The "lowest parent node" found is "the precursor node of X".
RBTNode<T> y = x.parent;
while ((y!=null) && (x==y.left)) {
x = y;
y = y.parent;
}
return y;
}
/*
* Rotate the node (x) of the red black tree to the left
*
* Left hand rotation diagram (left hand rotation of node x):
* px px
* / /
* x y
* / \ --(Left handed) -. / \#
* lx y x ry
* / \ / \
* ly ry lx ly
*
*
*/
private void leftRotate(RBTNode<T> x) {
// Set the right child of x to y
RBTNode<T> y = x.right;
// Set "left child of y" to "right child of x";
// If y's left child is not empty, set "x" to "Y's left child's father"
x.right = y.left;
if (y.left != null)
y.left.parent = x;
// Set "father of x" to "father of y"
y.parent = x.parent;
if (x.parent == null) {
this.mRoot = y; // If the parent of x is an empty node, set y as the root node
} else {
if (x.parent.left == x)
x.parent.left = y; // If x is the left child of its parent node, set y as the left child of X's parent node
else
x.parent.right = y; // If x is the left child of its parent node, set y as the left child of X's parent node
}
// Set "x" to "y's left child"
y.left = x;
// Set "parent of x" to "y"
x.parent = y;
}
/*
* Rotate the node (y) of the red black tree to the right
*
* Schematic diagram of right rotation (left rotation of node y):
* py py
* / /
* y x
* / \ --(Right handed) -. / \#
* x ry lx y
* / \ / \ #
* lx rx rx ry
*
*/
private void rightRotate(RBTNode<T> y) {
// Set x to be the left child of the current node.
RBTNode<T> x = y.left;
// Set "right child of x" to "left child of y";
// If "x's right child" is not empty, set "y" to "x's right child's father"
y.left = x.right;
if (x.right != null)
x.right.parent = y;
// Set "father of y" to "father of x"
x.parent = y.parent;
if (y.parent == null) {
this.mRoot = x; // If "y's father" is an empty node, set x as the root node
} else {
if (y == y.parent.right)
y.parent.right = x; // If y is the right child of its parent node, set x to "the right child of Y's parent node"
else
y.parent.left = x; // (y is the left child of its parent node) set x as "the left child of x's parent node"
}
// Set "y" to "right child of x"
x.right = y;
// Set "parent node of y" to "x"
y.parent = x;
}
/*
* Red black tree insertion correction function
*
* After inserting a node into the red black tree (out of balance), call this function again;
* The aim is to reshape it into a red black tree.
*
* Parameter Description:
* node The inserted node / / corresponds to z in introduction to algorithms
*/
private void insertFixUp(RBTNode<T> node) {
RBTNode<T> parent, gparent;
// If "the parent node exists and the color of the parent node is red"
while (((parent = parentOf(node))!=null) && isRed(parent)) {
gparent = parentOf(parent);
//If "parent node" is "left child of grandfather node"
if (parent == gparent.left) {
// Case 1 condition: the uncle node is red
RBTNode<T> uncle = gparent.right;
if ((uncle!=null) && isRed(uncle)) {
setBlack(uncle);
setBlack(parent);
setRed(gparent);
node = gparent;
continue;
}
// Case 2 condition: the uncle is black and the current node is the right child
if (parent.right == node) {
RBTNode<T> tmp;
leftRotate(parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 3 condition: the uncle is black and the current node is the left child.
setBlack(parent);
setRed(gparent);
rightRotate(gparent);
} else { //If "parent node of z" is "right child of grandfather node of z"
// Case 1 condition: the uncle node is red
RBTNode<T> uncle = gparent.left;
if ((uncle!=null) && isRed(uncle)) {
setBlack(uncle);
setBlack(parent);
setRed(gparent);
node = gparent;
continue;
}
// Case 2 condition: the uncle is black and the current node is the left child
if (parent.left == node) {
RBTNode<T> tmp;
rightRotate(parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 3 condition: the uncle is black and the current node is the right child.
setBlack(parent);
setRed(gparent);
leftRotate(gparent);
}
}
// Set the root node to black
setBlack(this.mRoot);
}
/*
* Insert the node into the red black tree
*
* Parameter Description:
* node The inserted node / / corresponds to the node in introduction to algorithms
*/
private void insert(RBTNode<T> node) {
int cmp;
RBTNode<T> y = null;
RBTNode<T> x = this.mRoot;
// 1. Treat the red black tree as a binary lookup tree and add nodes to the binary lookup tree.
while (x != null) {
y = x;
cmp = node.key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else
x = x.right;
}
node.parent = y;
if (y!=null) {
cmp = node.key.compareTo(y.key);
if (cmp < 0)
y.left = node;
else
y.right = node;
} else {
this.mRoot = node;
}
// 2. Set the color of the node to red
node.color = RED;
// 3. Revise it to a binary search tree
insertFixUp(node);
}
/*
* Create a new node (key) and insert it into the red black tree
*
* Parameter Description:
* key Insert key value of node
*/
public void insert(T key) {
RBTNode<T> node=new RBTNode<T>(key,BLACK,null,null,null);
// If the new node fails, return.
if (node != null)
insert(node);
}
/*
* Red black tree deletion correction function
*
* After deleting the inserted node from the red black tree (the red black tree is out of balance), call this function again;
* The aim is to reshape it into a red black tree.
*
* Parameter Description:
* node Nodes to be corrected
*/
private void removeFixUp(RBTNode<T> node, RBTNode<T> parent) {
RBTNode<T> other;
while ((node==null || isBlack(node)) && (node != this.mRoot)) {
if (parent.left == node) {
other = parent.right;
if (isRed(other)) {
// Case 1: x's brother w is red
setBlack(other);
setRed(parent);
leftRotate(parent);
other = parent.right;
}
if ((other.left==null || isBlack(other.left)) &&
(other.right==null || isBlack(other.right))) {
// Case 2: x's brother w is black, and w's two children are also black
setRed(other);
node = parent;
parent = parentOf(node);
} else {
if (other.right==null || isBlack(other.right)) {
// Case 3: x's brother w is black, and w's left child is red and right child is black.
setBlack(other.left);
setRed(other);
rightRotate(other);
other = parent.right;
}
// Case 4: x's brother w is black; And w's right child is red, and the left child is of any color.
setColor(other, colorOf(parent));
setBlack(parent);
setBlack(other.right);
leftRotate(parent);
node = this.mRoot;
break;
}
} else {
other = parent.left;
if (isRed(other)) {
// Case 1: x's brother w is red
setBlack(other);
setRed(parent);
rightRotate(parent);
other = parent.left;
}
if ((other.left==null || isBlack(other.left)) &&
(other.right==null || isBlack(other.right))) {
// Case 2: x's brother w is black, and w's two children are also black
setRed(other);
node = parent;
parent = parentOf(node);
} else {
if (other.left==null || isBlack(other.left)) {
// Case 3: x's brother w is black, and w's left child is red and right child is black.
setBlack(other.right);
setRed(other);
leftRotate(other);
other = parent.left;
}
// Case 4: x's brother w is black; And w's right child is red, and the left child is of any color.
setColor(other, colorOf(parent));
setBlack(parent);
setBlack(other.left);
rightRotate(parent);
node = this.mRoot;
break;
}
}
}
if (node!=null)
setBlack(node);
}
/*
* Delete the node and return the deleted node
*
* Parameter Description:
* node Deleted node
*/
private void remove(RBTNode<T> node) {
RBTNode<T> child, parent;
boolean color;
// The "left and right children are not empty" of the deleted node.
if ( (node.left!=null) && (node.right!=null) ) {
// The successor node of the deleted node. (called "replace node")
// Use it to replace the position of "deleted node", and then remove the "deleted node".
RBTNode<T> replace = node;
// Get successor node
replace = replace.right;
while (replace.left != null)
replace = replace.left;
// "Node node" is not a root node (only the root node does not have a parent node)
if (parentOf(node)!=null) {
if (parentOf(node).left == node)
parentOf(node).left = replace;
else
parentOf(node).right = replace;
} else {
// "Node node" is the root node. Update the root node.
this.mRoot = replace;
}
// Child is the right child of "replace node" and the node that needs to be "adjusted".
// There must be no left child in "replace node"! Because it is a successor node.
child = replace.right;
parent = parentOf(replace);
// Saves the color of the replace node
color = colorOf(replace);
// The deleted node is the parent node of its successor node
if (parent == node) {
parent = replace;
} else {
// child is not empty
if (child!=null)
setParent(child, parent);
parent.left = child;
replace.right = node.right;
setParent(node.right, replace);
}
replace.parent = node.parent;
replace.color = node.color;
replace.left = node.left;
node.left.parent = replace;
if (color == BLACK)
removeFixUp(child, parent);
node = null;
return ;
}
if (node.left !=null) {
child = node.left;
} else {
child = node.right;
}
parent = node.parent;
// Saves the color of the replace node
color = node.color;
if (child!=null)
child.parent = parent;
// 'node node' is not a root node
if (parent!=null) {
if (parent.left == node)
parent.left = child;
else
parent.right = child;
} else {
this.mRoot = child;
}
if (color == BLACK)
removeFixUp(child, parent);
node = null;
}
/*
* Delete node (z) and return the deleted node
*
* Parameter Description:
* tree Root node of red black tree
* z Deleted node
*/
public void remove(T key) {
RBTNode<T> node;
if ((node = search(mRoot, key)) != null)
remove(node);
}
/*
* Destruction of red and black trees
*/
private void destroy(RBTNode<T> tree) {
if (tree==null)
return ;
if (tree.left != null)
destroy(tree.left);
if (tree.right != null)
destroy(tree.right);
tree=null;
}
public void clear() {
destroy(mRoot);
mRoot = null;
}
/*
* Print "red black tree"
*
* key -- Key value of node
* direction -- 0,Indicates that the node is the root node;
* -1,Indicates that the node is the left child of its parent node;
* 1,Indicates that the node is the right child of its parent node.
*/
private void print(RBTNode<T> tree, T key, int direction) {
if(tree != null) {
if(direction==0) // tree is the root node
System.out.printf("%2d(B) is root\n", tree.key);
else // A tree is a branch node
System.out.printf("%2d(%s) is %2d's %6s child\n", tree.key, isRed(tree)?"R":"B", key, direction==1?"right" : "left");
print(tree.left, tree.key, -1);
print(tree.right,tree.key, 1);
}
}
public void print() {
if (mRoot != null)
print(mRoot, mRoot.key, 0);
}
}