Title Description

This topic comes from Force buckle , the difficulty is: difficulty, the title is described as follows:
Give you a string s and a character rule p, please implement a support '.' Matches the regular expression of '*'.

• ‘.’ Match any single character
• '*' matches zero or more preceding elements

The so-called matching is to cover the whole string s, not part of the string.

Example 1:

Input: s = "aa" p = "a"
Output: false
 Explanation:"a" Cannot match "aa" The entire string.

Example 2:

Input: s = "aa" p = "a*"
Output: true
 Explanation: because '*' Represents the one that can match zero or more preceding elements, The preceding element here is 'a'. Therefore, string "aa" Can be considered 'a' Again.

Example 3:

Input: s = "ab" p = ".*"
Output: true
 Explanation:".*" Indicates that zero or more can be matched('*')Any character('.'). 

Example 4:

Input: s = "aab" p = "c*a*b"
Output: true
 Explanation: because '*' Represents zero or more, here 'c' Is 0, 'a' Be repeated once. So you can match strings "aab". 

Example 5:

Input: s = "mississippi" p = "mis*is*p*."
Output: false

Tips:

• 0 <= s.length <= 20
• 0 <= p.length <= 30
• s may be empty and contain only lowercase letters from a-z.
• p may be empty and contain only lowercase letters from a-z and characters And *.
• Ensure that every time the character * appears, it is preceded by a valid character

Solution: dynamic programming method

thinking

If there is no character '*', directly traverse the character array of the string, and continue when two characters match, otherwise stop. This problem is very easy. However, for '*', the preceding characters can be matched 0 or 1 to more times (any time). There are many possible situations. At this time, the dynamic programming algorithm can be considered.
As we all know, the key to dealing with dynamic programming is to determine the state transition equation. For this topic, the state assumption is f[i][j], indicating whether the first I characters of s can match the first j characters of p. During state transition, consider the matching of the j-th character in p:

• If the j-th character of p is a lowercase letter of a-z, the matching of s[i] and p[j]:

  s[i]=p[j]，that f[i][j]=f[i-1][j-1];
  s[i]<>p[j]，that f[i][j]=false;
  

• If the j-th character of p is' * ', it is necessary to combine the j-1st character of p, which means that the j-1st character of p is matched any time:
  Match 0 times:

  	f[i][j]=f[i][j−2]
  

  In the case of matching 1, 2, 3,... Times, similarly, we have

  	f[i][j]=f[i−1][j−2],    if s[i]=p[j−1]
  	f[i][j]=f[i−2][j−2],    if s[i−1]=s[i]=p[j−1]
  	f[i][j]=f[i−3][j−2],    if s[i−2]=s[i−1]=s[i]=p[j−1]
  	⋯⋯
  

  Since there are many situations, it is not easy to list them one by one. From another angle, the combination of letters + asterisks can be summarized as follows:
  • 0 times, f[i][j]=f[i][j-2]; (at this time, s[i] and p[j-1] can be equal or unequal)
  • Appear one or more times, match the character at the end of S (s[i]=p[j-1]), remove the s[i] character, and the p[j-1] * combination can still continue to match with s[i-1], that is, if s[i]=p[j-1], f[i][j]=f[i-1][j]
    Therefore, the state transition equation can be written as: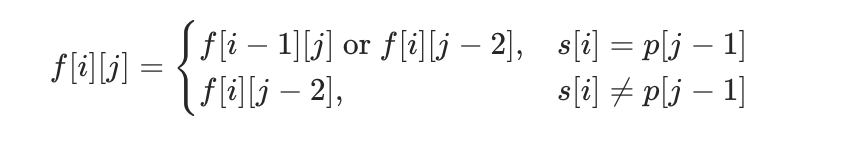
• If the jth character of p is', Then f[i][j]=true

The final state transition equation is:

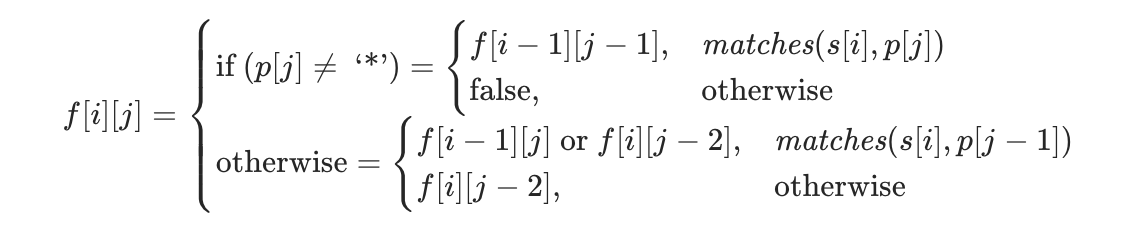
matches(x,y) is an auxiliary function to judge whether two characters match. Only if y is Or if x and y are the same, the two characters will match.

Note: f[0][0] =true, that is, two empty strings can be matched.

Problem solution

class Solution {
    public boolean isMatch(String s, String p) {
        int m = s.length();
        int n = p.length();
		//The reason why the array length is + 1 here is that s and p may be empty
        boolean[][] f = new boolean[m + 1][n + 1];
        f[0][0] = true;
        for (int i = 0; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (p.charAt(j - 1) == '*') {     
                    if (matches(s, p, i, j - 1)) {
                        f[i][j] = f[i][j - 2]|| f[i - 1][j];
                    }else{
                        f[i][j] = f[i][j - 2];
                    }
                } else {
                    if (matches(s, p, i, j)) {
                        f[i][j] = f[i - 1][j - 1];
                    }
                }
            }
        }
        return f[m][n];
    }

    public boolean matches(String s, String p, int i, int j) {
        if (i == 0) {
            return false;
        }
        //Because the two-dimensional array defined in the previous method loop considers that s and P are empty, when comparing whether the characters in line I and column j in f[i][j] are equal, it is actually necessary to judge whether s.charAt(i-1) and p.charAt(j-1) match
        if (p.charAt(j - 1) == '.') {//If p.charAt(j-1) is'. ', Then it must match
            return true;
        }
        return s.charAt(i - 1) == p.charAt(j - 1); //Match if two characters are equal
    }

}

Time complexity O(mn), space complexity O(mn)
reference resources:
[1]https://leetcode-cn.com/problems/regular-expression-matching/
[2]https://leetcode-cn.com/problems/regular-expression-matching/solution/zheng-ze-biao-da-shi-pi-pei-by-leetcode-solution/