preface
In many recent transformer work, we often mention a word: relative position bias. Used in the calculation of self attention. When I first saw this concept, I didn't understand its meaning. This paper is used to my own understanding of relative position bias.
The first time I saw the word was in swin transformer. Later, I saw it in both focal transformer and LG transformer.
Relative position bias
The basic form is as follows:
A
t
t
e
n
t
i
o
n
(
Q
,
K
,
V
)
=
S
o
f
t
m
a
x
(
Q
K
T
+
B
)
V
Attention(Q, K, V) = Softmax(QK^T + B)V
Attention(Q,K,V)=Softmax(QKT+B)V
among
Q
,
V
∈
R
n
×
d
Q, V \in R^{n\times d}
Q,V∈Rn×d,
B
∈
R
n
×
n
B \in R^{n \times n}
B∈Rn × n. N is the number of token vector s. It can be seen that the function of B is to give attention map
Q
K
T
QK^T
Each element of QKT adds a value. Its essence is to hope that the attention map will be further biased. Because the lower a value in the attention map, the lower the value after softmax. The contribution to the final feature is low.
B is not an arbitrarily initialized parameter. It has a complete use process. The basic process is as follows:
- Initialize a n 2 n^2 The tensor of n2 is used as a table and is also a parameter.
- Build a table index to look up the table according to the location. The details are described below
- Position lookup table is used in forward propagation.
- Back propagation update table.
In the source code of swin transformer, you can clearly see the use process of relative position offset.
In the constructor, there are the following related contents:
self.relative_position_bias_table = nn.Parameter(
torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1), num_heads)) # 2*Wh-1 * 2*Ww-1, nH
# get pair-wise relative position index for each token inside the window
coords_h = torch.arange(self.window_size[0])
coords_w = torch.arange(self.window_size[1])
coords = torch.stack(torch.meshgrid([coords_h, coords_w])) # 2, Wh, Ww
coords_flatten = torch.flatten(coords, 1) # 2, Wh*Ww
relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :] # 2, Wh*Ww, Wh*Ww
relative_coords = relative_coords.permute(1, 2, 0).contiguous() # Wh*Ww, Wh*Ww, 2
relative_coords[:, :, 0] += self.window_size[0] - 1 # shift to start from 0
relative_coords[:, :, 1] += self.window_size[1] - 1
relative_coords[:, :, 0] *= 2 * self.window_size[1] - 1
relative_position_index = relative_coords.sum(-1) # Wh*Ww, Wh*Ww
self.register_buffer("relative_position_index", relative_position_index)
The first row is the initialization table,
The following content is to create an index that can look up table parameters according to the relative position of query and key.
For example, now there is one
2
×
2
2 \times 2
two × Characteristic diagram of 2. Set the windows size to (2, 2), and we can see what the relative_position_index looks like:
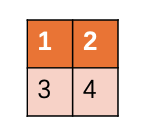
torch.Size([4, 4])
tensor([[4, 3, 1, 0],
[5, 4, 2, 1],
[7, 6, 4, 3],
[8, 7, 5, 4]])
Notice that the main diagonal is 4. The upper triangle is smaller than 4, and the lowest is 0; The lower triangle is larger than 4, and the maximum is 8; There are nine numbers in total, which is exactly equal to relative_ position_ bias_ Width and height of table.
Taking the first behavior as an example, the first element is 4 and the second element is 3; The correspondence is the positions labeled 1 and 2 in the grid.
In fact, both the first query and the first key are in the position of label 1, so if the relative position is 0, the fourth offset of the parameter table is used; The element in the second key is located in the right cell of label 1, using the first parameter of the parameter table.
Here's the point: as long as the query is in the left cell of 'key', it's relative_ position_ The corresponding positions in the index are all 3. Like the last number on the third line. The third line corresponds to label 3, only label 4 is on its right, and relative_position_bias_table[2][3] is exactly 3.
Then we can observe the position between other elements and find the same law. Therefore, it is not difficult to draw a conclusion that the value of B is related to the relative position of query and key. Query key pairs with consistent relative positions will use the same bias.
q = q * self.scale attn = (q @ k.transpose(-2, -1)) # Check the bias according to the relative position mapping provided by the index, and then generate the B that can be calculated with the attention map in the view relative_position_bias = self.relative_position_bias_table[self.relative_position_index.view(-1)].view( self.window_size[0] * self.window_size[1], self.window_size[0] * self.window_size[1], -1) # Wh*Ww,Wh*Ww,nH relative_position_bias = relative_position_bias.permute(2, 0, 1).contiguous() # nH, Wh*Ww, Wh*Ww attn = attn + relative_position_bias.unsqueeze(0)