- Leo-sam, published in IROS2020, is a very effective inertial laser tightly coupled odometer
- I'm going to get a laser odometer for our robot, so I'm going to change LIO-SAM and get it
- A problem is found in the modification process: in the process of odometer solution (LMOptimization function of mapOptimization), the author uses Euler angle to represent the rotating part of pose
- This is feasible for mobile robots, because in general, the pitch of ground mobile robots will not reach 90 °, which will not cause deadlock
- However, our robot is a climbing robot, which often turns over, so we can't use Euler angle to represent rotation; Therefore, this part needs to be modified
- Modification idea: "SO3 plus translation" is used to represent pose
- Let's take a look at the overall idea of the original code:
void laserCloudInfoHandler(const lio_sam::cloud_infoConstPtr& msgIn)
{
// extract time stamp
timeLaserInfoStamp = msgIn->header.stamp;
timeLaserInfoCur = msgIn->header.stamp.toSec();
// extract info and feature cloud
cloudInfo = *msgIn;
pcl::fromROSMsg(msgIn->cloud_corner, *laserCloudCornerLast);
pcl::fromROSMsg(msgIn->cloud_surface, *laserCloudSurfLast);
std::lock_guard<std::mutex> lock(mtx);
static double timeLastProcessing = -1;
if (timeLaserInfoCur - timeLastProcessing >= mappingProcessInterval)
{
timeLastProcessing = timeLaserInfoCur;
updateInitialGuess();
extractSurroundingKeyFrames();
downsampleCurrentScan();
scan2MapOptimization();
saveKeyFramesAndFactor();
correctPoses();
publishOdometry();
publishFrames();
}
}
- The general process of mapOptimization is as follows:
- updateInitialGuess: set the prediction result of IMU as the initial optimization value
- extractSurroundingKeyFrames: extract the key frame point cloud adjacent to the current frame to form a local map
- downsampleCurrentScan: downsampling, downsampling the corner and surface feature sets respectively
- scan2MapOptimization: focus!! Gauss Newton method is used to solve the pose of the current frame
- saveKeyFramesAndFactor: judge whether a new key frame needs to be inserted; Add new factors to iSAM for further optimization (the optimization effect is mainly reflected in error suppression in the case of long distance, long time and loopback)
- Correctpositions: fused with the pitch and roll predicted by IMU
- So, what I want to change is mainly scan2MapOptimization. Next, let's take a look at the main processes in scan2MapOptimization:
void scan2MapOptimization()
{
if (cloudKeyPoses3D->points.empty())
return;
if (laserCloudCornerLastDSNum > edgeFeatureMinValidNum && laserCloudSurfLastDSNum > surfFeatureMinValidNum)
{
kdtreeCornerFromMap->setInputCloud(laserCloudCornerFromMapDS);
kdtreeSurfFromMap->setInputCloud(laserCloudSurfFromMapDS);
for (int iterCount = 0; iterCount < 30; iterCount++)
{
laserCloudOri->clear();
coeffSel->clear();
cornerOptimization();
surfOptimization();
combineOptimizationCoeffs();
if (LMOptimization(iterCount) == true)
break;
}
transformUpdate();
} else {
ROS_WARN("Not enough features! Only %d edge and %d planar features available.", laserCloudCornerLastDSNum, laserCloudSurfLastDSNum);
}
}
- Translation:
- Feature matching, residual calculation and Jacobian calculation of translation part are carried out in corner optimization and surfoptimization (Jacobian of rotation part can be further calculated by Jacobian of translation part)
- Combineeoptimization coeffs combines the residuals calculated by the above two functions with some calculations of Jacobi, so that the same for can be used to calculate the iteration step in LMOptimization
- In LMOptimization, the Jacobian of the rotating part is calculated, and the Gauss Newton method is used to calculate an iterative step size and update the pose
- The content of the whole scan2MapOptimization is to optimize 30 iterations, and each iteration will re match the features
- OK, so what functions do I want to change?
- First and foremost: what I want to change is the representation of state variables in the optimization process
- The optimization iteration formula is as follows: J^T*J* δ x = - J^T * f(x), the representation of state variables will affect the calculation of Jacobi; In this paper, the representation of rotation is modified, so the functions involved in the calculation of rotation Jacobian should be modified, and the places where the state is updated should also be modified
- Therefore, we mainly modify the three functions: corner optimization, surfoptimization and LMOptimization
- First look at surfOptimization:
void surfOptimization()
{
// Update the pose of the current frame
updatePointAssociateToMap();
// Traverse the current frame plane point set
#pragma omp parallel for num_threads(numberOfCores)
for (int i = 0; i < laserCloudSurfLastDSNum; i++)
{
PointType pointOri, pointSel, coeff;
std::vector<int> pointSearchInd;
std::vector<float> pointSearchSqDis;
// Plane point (coordinate or lidar system)
pointOri = laserCloudSurfLastDS->points[i];
// According to the pose of the current frame, it is transformed to the world coordinate system (map system)
pointAssociateToMap(&pointOri, &pointSel);
// Find 5 plane points adjacent to the current plane point in the local plane point map
kdtreeSurfFromMap->nearestKSearch(pointSel, 5, pointSearchInd, pointSearchSqDis);
Eigen::Matrix<float, 5, 3> matA0;
Eigen::Matrix<float, 5, 1> matB0;
Eigen::Vector3f matX0;
matA0.setZero();
matB0.fill(-1);
matX0.setZero();
// The required distance is less than 1m
if (pointSearchSqDis[4] < 1.0) {
for (int j = 0; j < 5; j++) {
matA0(j, 0) = laserCloudSurfFromMapDS->points[pointSearchInd[j]].x;
matA0(j, 1) = laserCloudSurfFromMapDS->points[pointSearchInd[j]].y;
matA0(j, 2) = laserCloudSurfFromMapDS->points[pointSearchInd[j]].z;
}
// Assuming that the plane equation is ax+by+cz+1=0, here is the coefficient abc of the equation, d=1
matX0 = matA0.colPivHouseholderQr().solve(matB0);
// The coefficients of a plane equation are also components of the normal vector
float pa = matX0(0, 0);
float pb = matX0(1, 0);
float pc = matX0(2, 0);
float pd = 1;
// Unit normal vector
float ps = sqrt(pa * pa + pb * pb + pc * pc);
pa /= ps; pb /= ps; pc /= ps; pd /= ps;
// Check whether the plane is qualified. If the distance from one of the five points to the plane exceeds 0.2m, it is considered that these points are too scattered to form a plane
bool planeValid = true;
for (int j = 0; j < 5; j++) {
if (fabs(pa * laserCloudSurfFromMapDS->points[pointSearchInd[j]].x +
pb * laserCloudSurfFromMapDS->points[pointSearchInd[j]].y +
pc * laserCloudSurfFromMapDS->points[pointSearchInd[j]].z + pd) > 0.2) {
planeValid = false;
break;
}
}
// Plane qualified
if (planeValid) {
// Distance from current laser frame point to plane
float pd2 = pa * pointSel.x + pb * pointSel.y + pc * pointSel.z + pd;
float s = 1 - 0.9 * fabs(pd2) / sqrt(sqrt(pointSel.x * pointSel.x
+ pointSel.y * pointSel.y + pointSel.z * pointSel.z));
// Point to plane perpendicular unit normal vector (actually equivalent to plane normal vector)
coeff.x = s * pa;
coeff.y = s * pb;
coeff.z = s * pc;
// Distance from point to plane
coeff.intensity = s * pd2;
if (s > 0.1) {
// The plane points of the current laser frame are added to the matching set
laserCloudOriSurfVec[i] = pointOri;
// parameter
coeffSelSurfVec[i] = coeff;
laserCloudOriSurfFlag[i] = true;
}
}
}
}
}
- To sum up:
- First, turn the current feature point to the map coordinate system, and use the kd tree to find the five plane points adjacent to this point in the map
- Fit a plane with these five plane points and check whether the plane quality is good enough
- If the plane quality is good enough, calculate the point to face residual, and then assign a credibility factor to the residual according to the point to face distance (the credibility of the point far from the matched plane is not so high); If the confidence factor is large enough, put this point into the matching set
- Note the coeff variable. Its xyz stores the normal vector of the face (multiplied by a confidence factor), and its intensity stores the distance from the point (multiplied by a confidence factor) to the face
- Note here: according to the Jacobian calculation formula of point surface characteristics (SO3 plus translation version), the Jacobian of point surface residual to translation part is the unit normal vector transposition of this surface, and the Jacobian of rotation part is just an antisymmetric matrix of - RP (current rotation estimation multiplied by the representation of current point in radar coordinate system)
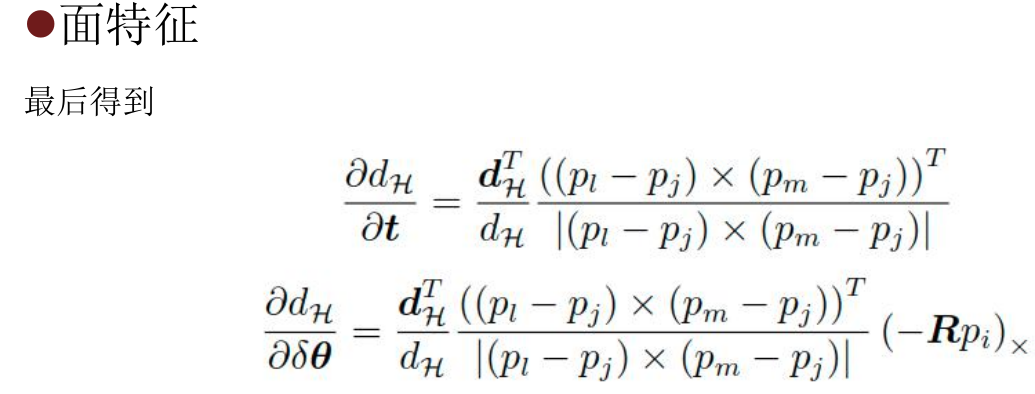
- The Jacobian calculation of the rotating part is completed in LMOptimization. We will complete the calculation of - Rp before LMOptimization
- Modified code:
Eigen::Vector3d CulRp(PointType const * const pi) {
return Eigen::Vector3d(transPointAssociateToMap(0,0) * pi->x + transPointAssociateToMap(0,1) * pi->y + transPointAssociateToMap(0,2) * pi->z,
transPointAssociateToMap(1,0) * pi->x + transPointAssociateToMap(1,1) * pi->y + transPointAssociateToMap(1,2) * pi->z,
transPointAssociateToMap(2,0) * pi->x + transPointAssociateToMap(2,1) * pi->y + transPointAssociateToMap(2,2) * pi->z);
}
void surfOptimization()
{
updatePointAssociateToMap();
#pragma omp parallel for num_threads(numberOfCores)
for (int i = 0; i < laserCloudSurfLastDSNum; i++)
{
PointType pointOri, pointSel, coeff;
std::vector<int> pointSearchInd;
std::vector<float> pointSearchSqDis;
pointOri = laserCloudSurfLastDS->points[i];
pointAssociateToMap(&pointOri, &pointSel);
kdtreeSurfFromMap->nearestKSearch(pointSel, 5, pointSearchInd, pointSearchSqDis);
Eigen::Matrix<float, 5, 3> matA0;
Eigen::Matrix<float, 5, 1> matB0;
Eigen::Vector3f matX0;
matA0.setZero();
matB0.fill(-1);
matX0.setZero();
if (pointSearchSqDis[4] < 1.0) {
for (int j = 0; j < 5; j++) {
matA0(j, 0) = laserCloudSurfFromMapDS->points[pointSearchInd[j]].x;
matA0(j, 1) = laserCloudSurfFromMapDS->points[pointSearchInd[j]].y;
matA0(j, 2) = laserCloudSurfFromMapDS->points[pointSearchInd[j]].z;
}
matX0 = matA0.colPivHouseholderQr().solve(matB0);
float pa = matX0(0, 0);
float pb = matX0(1, 0);
float pc = matX0(2, 0);
float pd = 1;
float ps = sqrt(pa * pa + pb * pb + pc * pc);
pa /= ps; pb /= ps; pc /= ps; pd /= ps;
bool planeValid = true;
for (int j = 0; j < 5; j++) {
if (fabs(pa * laserCloudSurfFromMapDS->points[pointSearchInd[j]].x +
pb * laserCloudSurfFromMapDS->points[pointSearchInd[j]].y +
pc * laserCloudSurfFromMapDS->points[pointSearchInd[j]].z + pd) > 0.2) {
planeValid = false;
break;
}
}
if (planeValid) {
float pd2 = pa * pointSel.x + pb * pointSel.y + pc * pointSel.z + pd;
float s = 1 - 0.9 * fabs(pd2) / sqrt(sqrt(pointSel.x * pointSel.x
+ pointSel.y * pointSel.y + pointSel.z * pointSel.z));
coeff.x = s * pa;
coeff.y = s * pb;
coeff.z = s * pc;
coeff.intensity = s * pd2;
if (s > 0.1) {
laserCloudOriSurfVec[i] = pointOri;
coeffSelSurfVec[i] = coeff;
laserCloudOriSurfFlag[i] = true;
surfRp[i] = (CulRp(&pointOri)); // New class member variable, STD:: vector < eigen:: Vector3D > surfrp// for jacobian orientation
}
}
}
}
}
- In fact, a line surfrp [i] = (culrp & pointori)) is added// New class member variable, STD:: vector < eigen:: Vector3D > surfrp// for jacobian orientation. . .
- The modification idea of corner optimization is similar to the above, but the Jacobian calculation of line features is different:

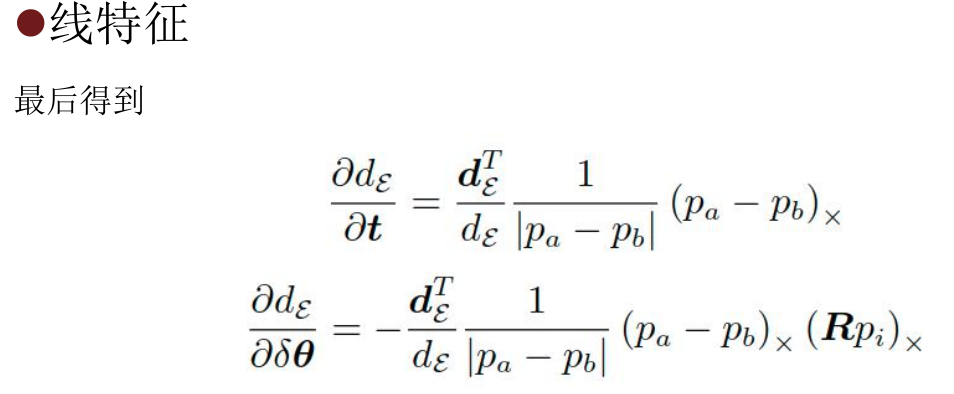 +Put the original code:
+Put the original code:
void cornerOptimization()
{
updatePointAssociateToMap();
#pragma omp parallel for num_threads(numberOfCores)
for (int i = 0; i < laserCloudCornerLastDSNum; i++)
{
PointType pointOri, pointSel, coeff;
std::vector<int> pointSearchInd;
std::vector<float> pointSearchSqDis;
pointOri = laserCloudCornerLastDS->points[i];
pointAssociateToMap(&pointOri, &pointSel);
kdtreeCornerFromMap->nearestKSearch(pointSel, 5, pointSearchInd, pointSearchSqDis);
cv::Mat matA1(3, 3, CV_32F, cv::Scalar::all(0));
cv::Mat matD1(1, 3, CV_32F, cv::Scalar::all(0));
cv::Mat matV1(3, 3, CV_32F, cv::Scalar::all(0));
if (pointSearchSqDis[4] < 1.0) {
float cx = 0, cy = 0, cz = 0;
for (int j = 0; j < 5; j++) {
cx += laserCloudCornerFromMapDS->points[pointSearchInd[j]].x;
cy += laserCloudCornerFromMapDS->points[pointSearchInd[j]].y;
cz += laserCloudCornerFromMapDS->points[pointSearchInd[j]].z;
}
cx /= 5; cy /= 5; cz /= 5;
float a11 = 0, a12 = 0, a13 = 0, a22 = 0, a23 = 0, a33 = 0;
for (int j = 0; j < 5; j++) {
float ax = laserCloudCornerFromMapDS->points[pointSearchInd[j]].x - cx;
float ay = laserCloudCornerFromMapDS->points[pointSearchInd[j]].y - cy;
float az = laserCloudCornerFromMapDS->points[pointSearchInd[j]].z - cz;
a11 += ax * ax; a12 += ax * ay; a13 += ax * az;
a22 += ay * ay; a23 += ay * az;
a33 += az * az;
}
a11 /= 5; a12 /= 5; a13 /= 5; a22 /= 5; a23 /= 5; a33 /= 5;
matA1.at<float>(0, 0) = a11; matA1.at<float>(0, 1) = a12; matA1.at<float>(0, 2) = a13;
matA1.at<float>(1, 0) = a12; matA1.at<float>(1, 1) = a22; matA1.at<float>(1, 2) = a23;
matA1.at<float>(2, 0) = a13; matA1.at<float>(2, 1) = a23; matA1.at<float>(2, 2) = a33;
cv::eigen(matA1, matD1, matV1);
if (matD1.at<float>(0, 0) > 3 * matD1.at<float>(0, 1)) {
float x0 = pointSel.x;
float y0 = pointSel.y;
float z0 = pointSel.z;
float x1 = cx + 0.1 * matV1.at<float>(0, 0);
float y1 = cy + 0.1 * matV1.at<float>(0, 1);
float z1 = cz + 0.1 * matV1.at<float>(0, 2);
float x2 = cx - 0.1 * matV1.at<float>(0, 0);
float y2 = cy - 0.1 * matV1.at<float>(0, 1);
float z2 = cz - 0.1 * matV1.at<float>(0, 2);
// a012 is actually ((p_i - p_a) x (p_i - p_b)).norm
float a012 = sqrt(((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1)) * ((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1))
+ ((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1)) * ((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1))
+ ((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1)) * ((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1)));
float l12 = sqrt((x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2) + (z1 - z2)*(z1 - z2)); // (pa - pb).norm
float la = ((y1 - y2)*((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1))
+ (z1 - z2)*((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1))) / a012 / l12;
float lb = -((x1 - x2)*((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1))
- (z1 - z2)*((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1))) / a012 / l12;
float lc = -((x1 - x2)*((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1))
+ (y1 - y2)*((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1))) / a012 / l12;
float ld2 = a012 / l12;
float s = 1 - 0.9 * fabs(ld2);
coeff.x = s * la;
coeff.y = s * lb;
coeff.z = s * lc;
coeff.intensity = s * ld2;
if (s > 0.1) {
laserCloudOriCornerVec[i] = pointOri;
coeffSelCornerVec[i] = coeff;
laserCloudOriCornerFlag[i] = true;
cornerRp[i] = CulRp(&pointOri);
}
}
}
}
}
- For the coeff variable of this function, its xyz directly stores the Jacobian of the translation part (multiplied by a credibility factor), and the intensity stores the distance from the point (multiplied by a credibility factor) to the line feature
- Note: in the Jacobian matrix of the rotating part of the line feature pair, Rp does not have a negative sign
- After modifying surfOptimization and cornereoptimization, because there are too many Rp calculations, Rp should also be merged together. Therefore, combine optimization coeffs should be changed:
void combineOptimizationCoeffs()
{
// combine corner coeffs
for (int i = 0; i < laserCloudCornerLastDSNum; ++i){
if (laserCloudOriCornerFlag[i] == true){
laserCloudOri->push_back(laserCloudOriCornerVec[i]);
coeffSel->push_back(coeffSelCornerVec[i]);
pcl::PointXYZ p;
p.x = cornerRp[i].x(); p.y = cornerRp[i].y(); p.z = cornerRp[i].z();
Rp->push_back(p); // pcl::PointCloud<pcl::PointXYZ>::Ptr Rp; // for jacobian orientation
}
}
// combine surf coeffs
for (int i = 0; i < laserCloudSurfLastDSNum; ++i){
if (laserCloudOriSurfFlag[i] == true){
laserCloudOri->push_back(laserCloudOriSurfVec[i]);
coeffSel->push_back(coeffSelSurfVec[i]);
pcl::PointXYZ p;
p.x = -1 * surfRp[i].x(); p.y = -1 * surfRp[i].y(); p.z = -1 * surfRp[i].z();
Rp->push_back(p);
}
}
// reset flag for next iteration
std::fill(laserCloudOriCornerFlag.begin(), laserCloudOriCornerFlag.end(), false);
std::fill(laserCloudOriSurfFlag.begin(), laserCloudOriSurfFlag.end(), false);
}
- If it is a line feature, add a negative sign to Rp
- Finally, to modify LMOptimization, start with the previous wave of source code:
bool LMOptimization(int iterCount)
{
// This optimization is from the original loam_velodyne by Ji Zhang, need to cope with coordinate transformation
// lidar <- camera --- camera <- lidar
// x = z --- x = y
// y = x --- y = z
// z = y --- z = x
// roll = yaw --- roll = pitch
// pitch = roll --- pitch = yaw
// yaw = pitch --- yaw = roll
// lidar -> camera
float srx = sin(transformTobeMapped[1]);
float crx = cos(transformTobeMapped[1]);
float sry = sin(transformTobeMapped[2]);
float cry = cos(transformTobeMapped[2]);
float srz = sin(transformTobeMapped[0]);
float crz = cos(transformTobeMapped[0]);
// There are too few matching feature points in the current frame
int laserCloudSelNum = laserCloudOri->size();
if (laserCloudSelNum < 50) {
return false;
}
cv::Mat matA(laserCloudSelNum, 6, CV_32F, cv::Scalar::all(0));
cv::Mat matAt(6, laserCloudSelNum, CV_32F, cv::Scalar::all(0));
cv::Mat matAtA(6, 6, CV_32F, cv::Scalar::all(0));
cv::Mat matB(laserCloudSelNum, 1, CV_32F, cv::Scalar::all(0));
cv::Mat matAtB(6, 1, CV_32F, cv::Scalar::all(0));
cv::Mat matX(6, 1, CV_32F, cv::Scalar::all(0));
PointType pointOri, coeff;
// Traverse matching feature points and construct Jacobian matrix
for (int i = 0; i < laserCloudSelNum; i++) {
// lidar -> camera todo
pointOri.x = laserCloudOri->points[i].y;
pointOri.y = laserCloudOri->points[i].z;
pointOri.z = laserCloudOri->points[i].x;
// lidar -> camera
coeff.x = coeffSel->points[i].y;
coeff.y = coeffSel->points[i].z;
coeff.z = coeffSel->points[i].x;
coeff.intensity = coeffSel->points[i].intensity;
// in camera
float arx = (crx*sry*srz*pointOri.x + crx*crz*sry*pointOri.y - srx*sry*pointOri.z) * coeff.x
+ (-srx*srz*pointOri.x - crz*srx*pointOri.y - crx*pointOri.z) * coeff.y
+ (crx*cry*srz*pointOri.x + crx*cry*crz*pointOri.y - cry*srx*pointOri.z) * coeff.z;
float ary = ((cry*srx*srz - crz*sry)*pointOri.x
+ (sry*srz + cry*crz*srx)*pointOri.y + crx*cry*pointOri.z) * coeff.x
+ ((-cry*crz - srx*sry*srz)*pointOri.x
+ (cry*srz - crz*srx*sry)*pointOri.y - crx*sry*pointOri.z) * coeff.z;
float arz = ((crz*srx*sry - cry*srz)*pointOri.x + (-cry*crz-srx*sry*srz)*pointOri.y)*coeff.x
+ (crx*crz*pointOri.x - crx*srz*pointOri.y) * coeff.y
+ ((sry*srz + cry*crz*srx)*pointOri.x + (crz*sry-cry*srx*srz)*pointOri.y)*coeff.z;
// lidar -> camera
matA.at<float>(i, 0) = arz;
matA.at<float>(i, 1) = arx;
matA.at<float>(i, 2) = ary;
matA.at<float>(i, 3) = coeff.z;
matA.at<float>(i, 4) = coeff.x;
matA.at<float>(i, 5) = coeff.y;
// The distance from point to straight line and plane is taken as the observation value
matB.at<float>(i, 0) = -coeff.intensity;
}
cv::transpose(matA, matAt);
matAtA = matAt * matA;
matAtB = matAt * matB;
// J^T·J·delta_x = -J^T · f Gauss Newton
cv::solve(matAtA, matAtB, matX, cv::DECOMP_QR);
// For the first iteration, check whether the approximate Hessian matrix (J^T · J) is degenerate or singular, and the determinant value = 0 todo
if (iterCount == 0) {
cv::Mat matE(1, 6, CV_32F, cv::Scalar::all(0));
cv::Mat matV(6, 6, CV_32F, cv::Scalar::all(0));
cv::Mat matV2(6, 6, CV_32F, cv::Scalar::all(0));
cv::eigen(matAtA, matE, matV);
matV.copyTo(matV2);
isDegenerate = false;
float eignThre[6] = {100, 100, 100, 100, 100, 100};
for (int i = 5; i >= 0; i--) {
if (matE.at<float>(0, i) < eignThre[i]) {
for (int j = 0; j < 6; j++) {
matV2.at<float>(i, j) = 0;
}
isDegenerate = true;
} else {
break;
}
}
matP = matV.inv() * matV2;
}
if (isDegenerate)
{
cv::Mat matX2(6, 1, CV_32F, cv::Scalar::all(0));
matX.copyTo(matX2);
matX = matP * matX2;
}
// Update current pose x = x + delta_x
transformTobeMapped[0] += matX.at<float>(0, 0);
transformTobeMapped[1] += matX.at<float>(1, 0);
transformTobeMapped[2] += matX.at<float>(2, 0);
transformTobeMapped[3] += matX.at<float>(3, 0);
transformTobeMapped[4] += matX.at<float>(4, 0);
transformTobeMapped[5] += matX.at<float>(5, 0);
float deltaR = sqrt(
pow(pcl::rad2deg(matX.at<float>(0, 0)), 2) +
pow(pcl::rad2deg(matX.at<float>(1, 0)), 2) +
pow(pcl::rad2deg(matX.at<float>(2, 0)), 2));
float deltaT = sqrt(
pow(matX.at<float>(3, 0) * 100, 2) +
pow(matX.at<float>(4, 0) * 100, 2) +
pow(matX.at<float>(5, 0) * 100, 2));
// delta_x is small and considered to converge
if (deltaR < 0.05 && deltaT < 0.05) {
return true;
}
return false;
}
- Place to change:
- State variables (state variables are defined as [roll, pitch, yaw, x, y, z], and this order will be temporarily modified during optimization)
- Jacobian matrix (matA is the Jacobian matrix, matAt is its transpose, matB is the residual), and matX is the iteration step size
- Status variable:
- From [roll, pitch, yaw, x, y, z] to [so3, x, y, z]
- Only when the optimization process is changed in this way, other parts still maintain the original representation; Therefore, there is a conversion process from Euler angle to SO3
- When updating the rotation, the rotation part of the iteration step needs to be transformed from Lie algebra to lie group, and then left multiplied to the original state
- After calculating the iteration, turn SO3 back to the Euler angle
- Jacobian matrix:
- There is no need to change the translation part, just change the rotation part
- Too lazy to write... Look at the code
bool LMOptimization(int iterCount)
{
// This optimization is from the original loam_velodyne by Ji Zhang, need to cope with coordinate transformation
// lidar <- camera --- camera <- lidar
// x = z --- x = y
// y = x --- y = z
// z = y --- z = x
// roll = yaw --- roll = pitch
// pitch = roll --- pitch = yaw
// yaw = pitch --- yaw = roll
// lidar -> camera
// float srx = sin(transformTobeMapped[1]);
// float crx = cos(transformTobeMapped[1]);
// float sry = sin(transformTobeMapped[2]);
// float cry = cos(transformTobeMapped[2]);
// float srz = sin(transformTobeMapped[0]);
// float crz = cos(transformTobeMapped[0]);
int laserCloudSelNum = laserCloudOri->size();
if (laserCloudSelNum < 50) {
return false;
}
cv::Mat matA(laserCloudSelNum, 6, CV_32F, cv::Scalar::all(0));
cv::Mat matAt(6, laserCloudSelNum, CV_32F, cv::Scalar::all(0));
cv::Mat matAtA(6, 6, CV_32F, cv::Scalar::all(0));
cv::Mat matB(laserCloudSelNum, 1, CV_32F, cv::Scalar::all(0));
cv::Mat matAtB(6, 1, CV_32F, cv::Scalar::all(0));
cv::Mat matX(6, 1, CV_32F, cv::Scalar::all(0));
PointType pointOri, coeff;
for (int i = 0; i < laserCloudSelNum; i++) {
// // lidar -> camera
// pointOri.x = laserCloudOri->points[i].y;
// pointOri.y = laserCloudOri->points[i].z;
// pointOri.z = laserCloudOri->points[i].x;
// // lidar -> camera
// coeff.x = coeffSel->points[i].y;
// coeff.y = coeffSel->points[i].z;
// coeff.z = coeffSel->points[i].x;
// coeff.intensity = coeffSel->points[i].intensity;
// lidar -> camera
pointOri.x = laserCloudOri->points[i].x;
pointOri.y = laserCloudOri->points[i].y;
pointOri.z = laserCloudOri->points[i].z;
// lidar -> camera
coeff.x = coeffSel->points[i].x;
coeff.y = coeffSel->points[i].y;
coeff.z = coeffSel->points[i].z;
coeff.intensity = coeffSel->points[i].intensity;
// skew of Rp
auto p_pcl = Rp->points[i];
Eigen::Vector3f p(p_pcl.x, p_pcl.y, p_pcl.z);
Eigen::Matrix3f RpSkew = mapOptimization::skewSymmetric(p);
Eigen::Vector3f tmp(coeff.x, coeff.y, coeff.z);
Eigen::Matrix<float, 1, 3> jacobian_theta = tmp.transpose() * RpSkew;
// // in camera
// float arx = (crx*sry*srz*pointOri.x + crx*crz*sry*pointOri.y - srx*sry*pointOri.z) * coeff.x
// + (-srx*srz*pointOri.x - crz*srx*pointOri.y - crx*pointOri.z) * coeff.y
// + (crx*cry*srz*pointOri.x + crx*cry*crz*pointOri.y - cry*srx*pointOri.z) * coeff.z;
//
// float ary = ((cry*srx*srz - crz*sry)*pointOri.x
// + (sry*srz + cry*crz*srx)*pointOri.y + crx*cry*pointOri.z) * coeff.x
// + ((-cry*crz - srx*sry*srz)*pointOri.x
// + (cry*srz - crz*srx*sry)*pointOri.y - crx*sry*pointOri.z) * coeff.z;
//
// float arz = ((crz*srx*sry - cry*srz)*pointOri.x + (-cry*crz-srx*sry*srz)*pointOri.y)*coeff.x
// + (crx*crz*pointOri.x - crx*srz*pointOri.y) * coeff.y
// + ((sry*srz + cry*crz*srx)*pointOri.x + (crz*sry-cry*srx*srz)*pointOri.y)*coeff.z;
// // lidar -> camera
// matA.at<float>(i, 0) = arz;
// matA.at<float>(i, 1) = arx;
// matA.at<float>(i, 2) = ary;
matA.at<float>(i, 0) = jacobian_theta(0, 0);
matA.at<float>(i, 1) = jacobian_theta(0, 1);
matA.at<float>(i, 2) = jacobian_theta(0, 2);
// matA.at<float>(i, 3) = coeff.z;
// matA.at<float>(i, 4) = coeff.x;
// matA.at<float>(i, 5) = coeff.y;
matA.at<float>(i, 3) = coeff.x;
matA.at<float>(i, 4) = coeff.y;
matA.at<float>(i, 5) = coeff.z;
matB.at<float>(i, 0) = -coeff.intensity;
}
cv::transpose(matA, matAt);
matAtA = matAt * matA;
matAtB = matAt * matB;
cv::solve(matAtA, matAtB, matX, cv::DECOMP_QR);
if (iterCount == 0) {
cv::Mat matE(1, 6, CV_32F, cv::Scalar::all(0));
cv::Mat matV(6, 6, CV_32F, cv::Scalar::all(0));
cv::Mat matV2(6, 6, CV_32F, cv::Scalar::all(0));
cv::eigen(matAtA, matE, matV);
matV.copyTo(matV2);
isDegenerate = false;
float eignThre[6] = {100, 100, 100, 100, 100, 100};
for (int i = 5; i >= 0; i--) {
if (matE.at<float>(0, i) < eignThre[i]) {
for (int j = 0; j < 6; j++) {
matV2.at<float>(i, j) = 0;
}
isDegenerate = true;
} else {
break;
}
}
matP = matV.inv() * matV2;
}
if (isDegenerate)
{
cv::Mat matX2(6, 1, CV_32F, cv::Scalar::all(0));
matX.copyTo(matX2);
matX = matP * matX2;
}
Eigen::Quaternionf quat(transPointAssociateToMap.matrix().block<3, 3>(0, 0));
Sophus::SO3f so3_orientation;
so3_orientation.setQuaternion(quat.normalized());
// transformTobeMapped[0] += matX.at<float>(0, 0);
// transformTobeMapped[1] += matX.at<float>(1, 0);
// transformTobeMapped[2] += matX.at<float>(2, 0);
// transformTobeMapped[3] += matX.at<float>(3, 0);
// transformTobeMapped[4] += matX.at<float>(4, 0);
// transformTobeMapped[5] += matX.at<float>(5, 0);
Eigen::Vector3f update_so3(matX.at<float>(0, 0), matX.at<float>(1, 0), matX.at<float>(2, 0));
so3_orientation = Sophus::SO3f::exp(update_so3) * so3_orientation;
Eigen::Vector3f euler_angles = so3_orientation.matrix().eulerAngles(2, 1, 0);
transformTobeMapped[0] = euler_angles[2];
transformTobeMapped[1] = euler_angles[1];
transformTobeMapped[2] = euler_angles[0];
transformTobeMapped[3] += matX.at<float>(3, 0);
transformTobeMapped[4] += matX.at<float>(4, 0);
transformTobeMapped[5] += matX.at<float>(5, 0);
// float deltaR = sqrt(
// pow(pcl::rad2deg(matX.at<float>(0, 0)), 2) +
// pow(pcl::rad2deg(matX.at<float>(1, 0)), 2) +
// pow(pcl::rad2deg(matX.at<float>(2, 0)), 2));
auto tmp = Sophus::SO3f::exp(update_so3);
float deltaR = sqrt(
pow(pcl::rad2deg(tmp.angleX()), 2) +
pow(pcl::rad2deg(tmp.angleY()), 2) +
pow(pcl::rad2deg(tmp.angleZ()), 2));
float deltaT = sqrt(
pow(matX.at<float>(3, 0) * 100, 2) +
pow(matX.at<float>(4, 0) * 100, 2) +
pow(matX.at<float>(5, 0) * 100, 2));
if (deltaR < 0.05 && deltaT < 0.05) {
return true; // converged
}
return false; // keep optimizing
}
- There will be problems when SO3 is integrated with IMU after turning back to Euler angle (which may involve Euler angle interpolation). Therefore, I change transformUpdate in scan2MapOptimization to incrementalOdometryAffineBack = trans2Affine3f(transformTobeMapped);, In this way, it will not be integrated with the pitch and roll of IMU
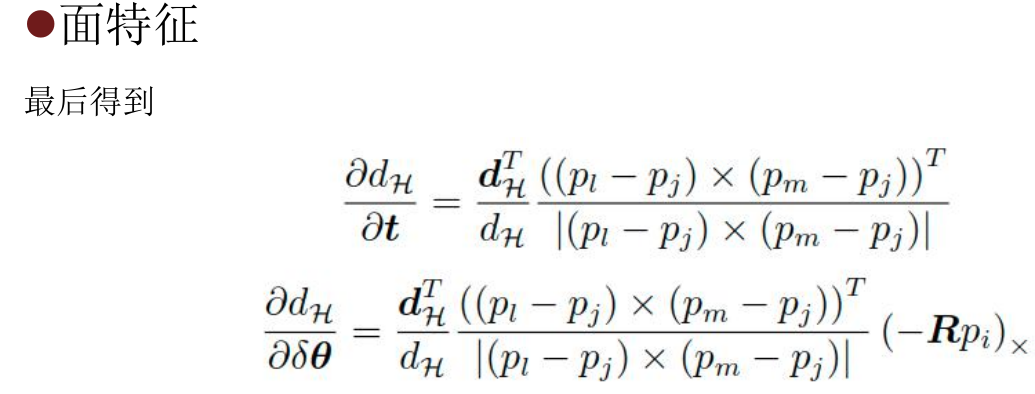

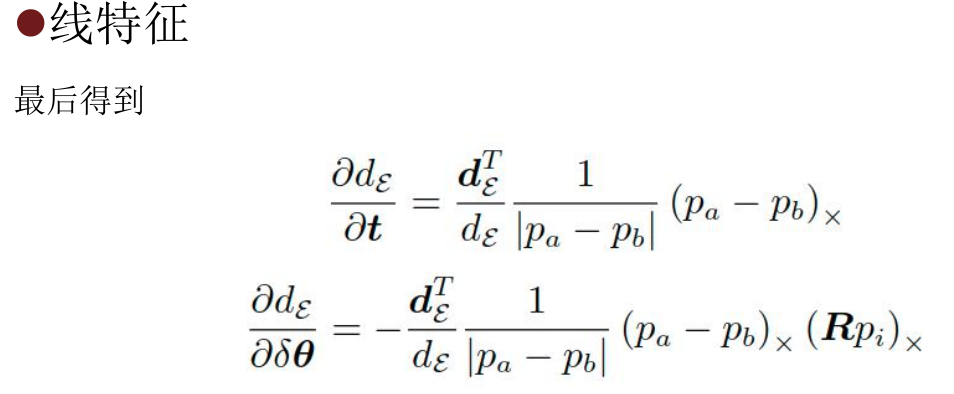 +Put the original code:
+Put the original code: