Enigma comes from Greek and is interpreted in English as "a mystery, an incomprehensible thing".
-- Excerpt from Ele Laboratory
As we know, enigma machine is an important information encryption machine of the German army in World War II, which has many characteristics.
First of all, it is an all-in-one encryption and decryption machine
Secondly, it is exclusive. Although different ciphertexts may be obtained by inputting the same plaintext many times, plaintext a can never be encrypted as itself. This perfect concealment of the nature of the plaintext itself was caused by the reflector, but it was finally used by Turing to give a fatal blow to the enigma machine.
Enigma machine has many different models, such as 3-wheel type, 5-wheel type, 5-wheel type, 3-wheel type and so on. I repeat the program of three wheel Enigma machine. What needs to be explained is that because the essence of enigma is the rotor and the reflector, the code also repeats this process, and the wiring board is omitted. After all, the power of Enigma machine is that it is so crazy that it almost abnormal that it can almost "change the table word by word", and the terminal block is only a simple letter replacement, which is nothing new in itself.
Don't say much, just go to the code: (see the end of the text for some instructions)
# -*- coding: utf-8 -*-
"""
Created on Tue Jan 4 09:40:42 2022
@author: burger
"""
from numpy import random
import numpy as np
import time
arr = np.array(['a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z'])
#Enter a batch number
num = input('Please enter the name you want to use enigma Machine batch number XXX-XXX-XXX(Example: 123-456-789)\n')
filename = 'enigma_code_book.txt'
with open(filename) as file_object:
context = file_object.read()
if num in context:
number = context.find(num)
arr_a=context[(number+12):(number+38)] #Runner 1
arr_b=context[(number+39):(number+65)] #Runner 2
arr_c=context[(number+66):(number+92)] #Runner 3
arr_d=context[(number+93):(number+119)] #Reflector
else:
arr_a=random.permutation(arr)
arr_b=random.permutation(arr)
arr_c=random.permutation(arr)
arr_d=random.permutation(arr)
with open(filename,'a') as file_object:
str_1='\n'
str_1=str_1+num
str_1+=' '
for i in range(len(arr_a)):
str_1+=arr_a[i]
str_1+=' '
for i in range(len(arr_b)):
str_1+=arr_b[i]
str_1+=' '
for i in range(len(arr_c)):
str_1+=arr_c[i]
str_1+=' '
for i in range(len(arr_d)):
str_1+=arr_d[i]
str_1+=' '
file_object.write(str_1)
zzwz=input('Please enter the initial rotor position(The specification is three English letters with two English commas in the middle)\n eg: a,b,c\n')#zzwz is the rotor position
zz_1=list(zzwz)[0]
zz_2=list(zzwz)[2]
zz_3=list(zzwz)[4]
num_zz_1=ord(zz_1)-97
num_zz_2=ord(zz_2)-97
num_zz_3=ord(zz_3)-97
def main():
global num_zz_1
global num_zz_2
global num_zz_3
text=input('Please enter the encrypted content\n')
for n in range(len(text)):
string=list(text)[n]
print(zhuanhuan(string),end='')
num_zz_1+=1
if num_zz_1 == 26:
num_zz_1 = 0
num_zz_2+=1
if num_zz_2 == 26:
num_zz_2=0
num_zz_3+=1
if num_zz_3 == 26:
num_zz_3 = 0
def zhuanhuan(letter):
#Runner a
#There are 26 contacts on the right
#Random connection mode for generating round a
a_1_1=False
a_1_2=False
a_1_3=False
a_1_4=False
a_1_5=False
a_1_6=False
a_1_7=False
a_1_8=False
a_1_9=False
a_1_10=False
a_1_11=False
a_1_12=False
a_1_13=False
a_1_14=False
a_1_15=False
a_1_16=False
a_1_17=False
a_1_18=False
a_1_19=False
a_1_20=False
a_1_21=False
a_1_22=False
a_1_23=False
a_1_24=False
a_1_25=False
a_1_26=False
if letter == 'a':
a_1_1 = True
if letter == 'b':
a_1_2 = True
elif letter == 'c':
a_1_3 = True
elif letter == 'd':
a_1_4 = True
elif letter == 'e':
a_1_5 = True
elif letter == 'f':
a_1_6 = True
elif letter == 'g':
a_1_7 = True
elif letter == 'h':
a_1_8 = True
elif letter == 'i':
a_1_9 = True
elif letter == 'j':
a_1_10 = True
elif letter == 'k':
a_1_11 = True
elif letter == 'l':
a_1_12 = True
elif letter == 'm':
a_1_13 = True
elif letter == 'n':
a_1_14 = True
elif letter == 'o':
a_1_15 = True
elif letter == 'p':
a_1_16 = True
elif letter == 'q':
a_1_17 = True
elif letter == 'r':
a_1_18 = True
elif letter == 's':
a_1_19 = True
elif letter == 't':
a_1_20 = True
elif letter == 'u':
a_1_21 = True
elif letter == 'v':
a_1_22 = True
elif letter == 'w':
a_1_23 = True
elif letter == 'x':
a_1_24 = True
elif letter == 'y':
a_1_25 = True
elif letter == 'z':
a_1_26 = True
a_1_first=[a_1_1,a_1_2,a_1_3,a_1_4,a_1_5,a_1_6,a_1_7,a_1_8,a_1_9,a_1_10,a_1_11,a_1_12,a_1_13,a_1_14,a_1_15,a_1_16,a_1_17,a_1_18,a_1_19,a_1_20,a_1_21,a_1_22,a_1_23,a_1_24,a_1_25,a_1_26]
# print(a_1_first)
a_1=[False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False,False]
for i in range(26):
global num_zz_1
a_1[i]=a_1_first[(num_zz_1-26)+i]
# print(a_1)
#There are 26 contacts on the left side
a_2_1=False
a_2_2=False
a_2_3=False
a_2_4=False
a_2_5=False
a_2_6=False
a_2_7=False
a_2_8=False
a_2_9=False
a_2_10=False
a_2_11=False
a_2_12=False
a_2_13=False
a_2_14=False
a_2_15=False
a_2_16=False
a_2_17=False
a_2_18=False
a_2_19=False
a_2_20=False
a_2_21=False
a_2_22=False
a_2_23=False
a_2_24=False
a_2_25=False
a_2_26=False
a_2=[a_2_1,a_2_2,a_2_3,a_2_4,a_2_5,a_2_6,a_2_7,a_2_8,a_2_9,a_2_10,a_2_11,a_2_12,a_2_13,a_2_14,a_2_15,a_2_16,a_2_17,a_2_18,a_2_19,a_2_20,a_2_21,a_2_22,a_2_23,a_2_24,a_2_25,a_2_26]
#Build the left-right correspondence of runner a
for i in range(26):
a_2[i]=a_1[ord(arr_a[i])-97]
# print(a_2)
#At this time, the modeling of runner a is successful
#Runner b
#There are 26 contacts on the right
b_1_1=False
b_1_2=False
b_1_3=False
b_1_4=False
b_1_5=False
b_1_6=False
b_1_7=False
b_1_8=False
b_1_9=False
b_1_10=False
b_1_11=False
b_1_12=False
b_1_13=False
b_1_14=False
b_1_15=False
b_1_16=False
b_1_17=False
b_1_18=False
b_1_19=False
b_1_20=False
b_1_21=False
b_1_22=False
b_1_23=False
b_1_24=False
b_1_25=False
b_1_26=False
b_1=[b_1_1,b_1_2,b_1_3,b_1_4,b_1_5,b_1_6,b_1_7,b_1_8,b_1_9,b_1_10,b_1_11,b_1_12,b_1_13,b_1_14,b_1_15,b_1_16,b_1_17,b_1_18,b_1_19,b_1_20,b_1_21,b_1_22,b_1_23,b_1_24,b_1_25,b_1_26]
#Wheel a to wheel b
for i in range(26):
global num_zz_2
b_1[i]=a_2[((num_zz_2)-26)+i]
# print(b_1)
#There are 26 contacts on the left
b_2_1=False
b_2_2=False
b_2_3=False
b_2_4=False
b_2_5=False
b_2_6=False
b_2_7=False
b_2_8=False
b_2_9=False
b_2_10=False
b_2_11=False
b_2_12=False
b_2_13=False
b_2_14=False
b_2_15=False
b_2_16=False
b_2_17=False
b_2_18=False
b_2_19=False
b_2_20=False
b_2_21=False
b_2_22=False
b_2_23=False
b_2_24=False
b_2_25=False
b_2_26=False
b_2=[b_2_1,b_2_2,b_2_3,b_2_4,b_2_5,b_2_6,b_2_7,b_2_8,b_2_9,b_2_10,b_2_11,b_2_12,b_2_13,b_2_14,b_2_15,b_2_16,b_2_17,b_2_18,b_2_19,b_2_20,b_2_21,b_2_22,b_2_23,b_2_24,b_2_25,b_2_26]
#Build the left-right correspondence of runner b
for i in range(26):
b_2[i]=b_1[ord(arr_b[i])-97]
# print(b_2)
#At this time, the modeling of runner b is successful
#Runner c
#There are 26 contacts on the right
c_1_1=False
c_1_2=False
c_1_3=False
c_1_4=False
c_1_5=False
c_1_6=False
c_1_7=False
c_1_8=False
c_1_9=False
c_1_10=False
c_1_11=False
c_1_12=False
c_1_13=False
c_1_14=False
c_1_15=False
c_1_16=False
c_1_17=False
c_1_18=False
c_1_19=False
c_1_20=False
c_1_21=False
c_1_22=False
c_1_23=False
c_1_24=False
c_1_25=False
c_1_26=False
c_1=[c_1_1,c_1_2,c_1_3,c_1_4,c_1_5,c_1_6,c_1_7,c_1_8,c_1_9,c_1_10,c_1_11,c_1_12,c_1_13,c_1_14,c_1_15,c_1_16,c_1_17,c_1_18,c_1_19,c_1_20,c_1_21,c_1_22,c_1_23,c_1_24,c_1_25,c_1_26]
#Wheel b to wheel c
for i in range(26):
global num_zz_3
c_1[i]=b_2[((num_zz_3)-26)+i]
# print(c_1)
#There are 26 contacts on the left
c_2_1=False
c_2_2=False
c_2_3=False
c_2_4=False
c_2_5=False
c_2_6=False
c_2_7=False
c_2_8=False
c_2_9=False
c_2_10=False
c_2_11=False
c_2_12=False
c_2_13=False
c_2_14=False
c_2_15=False
c_2_16=False
c_2_17=False
c_2_18=False
c_2_19=False
c_2_20=False
c_2_21=False
c_2_22=False
c_2_23=False
c_2_24=False
c_2_25=False
c_2_26=False
c_2=[c_2_1,c_2_2,c_2_3,c_2_4,c_2_5,c_2_6,c_2_7,c_2_8,c_2_9,c_2_10,c_2_11,c_2_12,c_2_13,c_2_14,c_2_15,c_2_16,c_2_17,c_2_18,c_2_19,c_2_20,c_2_21,c_2_22,c_2_23,c_2_24,c_2_25,c_2_26]
#Build the left-right correspondence of runner c
for i in range(26):
c_2[i]=c_1[ord(arr_c[i])-97]
# print(c_2)
#At this time, the modeling of runner c is successful
#c runner reflector
for i in range(0,26,2):
c_2[ord(arr_d[i])-97],c_2[ord(arr_d[i+1])-97]=c_2[ord(arr_d[i+1])-97],c_2[ord(arr_d[i])-97]
#Back propagation
arr_c_2=[]
arr_b_2=[]
arr_a_2=[]
arr_c_1=[]
arr_b_1=[]
arr_a_1=[]
for i in range(26):
arr_c_2.append(ord(arr_c[i])-97)
arr_b_2.append(ord(arr_b[i])-97)
arr_a_2.append(ord(arr_a[i])-97)
arr_c_0=sorted(arr_c_2)
arr_b_0=sorted(arr_b_2)
arr_a_0=sorted(arr_a_2)
for i in range(26):
arr_c_1.append(arr_c_2.index(arr_c_0[i]))
arr_b_1.append(arr_b_2.index(arr_c_0[i]))
arr_a_1.append(arr_a_2.index(arr_c_0[i]))
#Runner c back propagation
c_3_1=False
c_3_2=False
c_3_3=False
c_3_4=False
c_3_5=False
c_3_6=False
c_3_7=False
c_3_8=False
c_3_9=False
c_3_10=False
c_3_11=False
c_3_12=False
c_3_13=False
c_3_14=False
c_3_15=False
c_3_16=False
c_3_17=False
c_3_18=False
c_3_19=False
c_3_20=False
c_3_21=False
c_3_22=False
c_3_23=False
c_3_24=False
c_3_25=False
c_3_26=False
c_3=[c_3_1,c_3_2,c_3_3,c_3_4,c_3_5,c_3_6,c_3_7,c_3_8,c_3_9,c_3_10,c_3_11,c_3_12,c_3_13,c_3_14,c_3_15,c_3_16,c_3_17,c_3_18,c_3_19,c_3_20,c_3_21,c_3_22,c_3_23,c_3_24,c_3_25,c_3_26]
for i in range(26):
c_3[i]=c_2[arr_c_1[i]]
# print(c_3)
#Wheel c to wheel b
b_3_1=False
b_3_2=False
b_3_3=False
b_3_4=False
b_3_5=False
b_3_6=False
b_3_7=False
b_3_8=False
b_3_9=False
b_3_10=False
b_3_11=False
b_3_12=False
b_3_13=False
b_3_14=False
b_3_15=False
b_3_16=False
b_3_17=False
b_3_18=False
b_3_19=False
b_3_20=False
b_3_21=False
b_3_22=False
b_3_23=False
b_3_24=False
b_3_25=False
b_3_26=False
b_3=[b_3_1,b_3_2,b_3_3,b_3_4,b_3_5,b_3_6,b_3_7,b_3_8,b_3_9,b_3_10,b_3_11,b_3_12,b_3_13,b_3_14,b_3_15,b_3_16,b_3_17,b_3_18,b_3_19,b_3_20,b_3_21,b_3_22,b_3_23,b_3_24,b_3_25,b_3_26]
for i in range(26):
# global num_zz_3
b_3[i]=c_3[-(num_zz_3)+i]#There are 26 contacts on the left
# print(b_3)
#Runner b back propagation
b_4_1=False
b_4_2=False
b_4_3=False
b_4_4=False
b_4_5=False
b_4_6=False
b_4_7=False
b_4_8=False
b_4_9=False
b_4_10=False
b_4_11=False
b_4_12=False
b_4_13=False
b_4_14=False
b_4_15=False
b_4_16=False
b_4_17=False
b_4_18=False
b_4_19=False
b_4_20=False
b_4_21=False
b_4_22=False
b_4_23=False
b_4_24=False
b_4_25=False
b_4_26=False
b_4=[b_4_1,b_4_2,b_4_3,b_4_4,b_4_5,b_4_6,b_4_7,b_4_8,b_4_9,b_4_10,b_4_11,b_4_12,b_4_13,b_4_14,b_4_15,b_4_16,b_4_17,b_4_18,b_4_19,b_4_20,b_4_21,b_4_22,b_4_23,b_4_24,b_4_25,b_4_26]
for i in range(26):
b_4[i]=b_3[arr_b_1[i]]
# print(b_4)
#Wheel b to wheel a
a_3_1=False
a_3_2=False
a_3_3=False
a_3_4=False
a_3_5=False
a_3_6=False
a_3_7=False
a_3_8=False
a_3_9=False
a_3_10=False
a_3_11=False
a_3_12=False
a_3_13=False
a_3_14=False
a_3_15=False
a_3_16=False
a_3_17=False
a_3_18=False
a_3_19=False
a_3_20=False
a_3_21=False
a_3_22=False
a_3_23=False
a_3_24=False
a_3_25=False
a_3_26=False
a_3=[a_3_1,a_3_2,a_3_3,a_3_4,a_3_5,a_3_6,a_3_7,a_3_8,a_3_9,a_3_10,a_3_11,a_3_12,a_3_13,a_3_14,a_3_15,a_3_16,a_3_17,a_3_18,a_3_19,a_3_20,a_3_21,a_3_22,a_3_23,a_3_24,a_3_25,a_3_26]
for i in range(26):
# global num_zz_2
a_3[i]=b_4[-(num_zz_2)+i]#There are 26 contacts on the left
# print(a_3)
#Runner a back propagation
a_4_1=False
a_4_2=False
a_4_3=False
a_4_4=False
a_4_5=False
a_4_6=False
a_4_7=False
a_4_8=False
a_4_9=False
a_4_10=False
a_4_11=False
a_4_12=False
a_4_13=False
a_4_14=False
a_4_15=False
a_4_16=False
a_4_17=False
a_4_18=False
a_4_19=False
a_4_20=False
a_4_21=False
a_4_22=False
a_4_23=False
a_4_24=False
a_4_25=False
a_4_26=False
a_4=[a_4_1,a_4_2,a_4_3,a_4_4,a_4_5,a_4_6,a_4_7,a_4_8,a_4_9,a_4_10,a_4_11,a_4_12,a_4_13,a_4_14,a_4_15,a_4_16,a_4_17,a_4_18,a_4_19,a_4_20,a_4_21,a_4_22,a_4_23,a_4_24,a_4_25,a_4_26]
for i in range(26):
a_4[i]=a_3[arr_a_1[i]]
# print(a_4)
#Round a return
z_3_1=False
z_3_2=False
z_3_3=False
z_3_4=False
z_3_5=False
z_3_6=False
z_3_7=False
z_3_8=False
z_3_9=False
z_3_10=False
z_3_11=False
z_3_12=False
z_3_13=False
z_3_14=False
z_3_15=False
z_3_16=False
z_3_17=False
z_3_18=False
z_3_19=False
z_3_20=False
z_3_21=False
z_3_22=False
z_3_23=False
z_3_24=False
z_3_25=False
z_3_26=False
z_3=[z_3_1,z_3_2,z_3_3,z_3_4,z_3_5,z_3_6,z_3_7,z_3_8,z_3_9,z_3_10,z_3_11,z_3_12,z_3_13,z_3_14,z_3_15,z_3_16,z_3_17,z_3_18,z_3_19,z_3_20,z_3_21,z_3_22,z_3_23,z_3_24,z_3_25,z_3_26]
for i in range(26):
# global num_zz_1
z_3[i]=a_4[-(num_zz_1)+i]
# print(z_3)
for i in range(26):
if z_3[i]==True:
return(chr(i+97))
if __name__ == '__main__':
main()Briefly explain the code. The general idea is to use a boolean type list to represent the power on or power off of each group of 26 contacts. In the process of reproduction, Turing used an idea when cracking the Enigma machine: place the two enigma machines with completely symmetrical wiring side by side. Among them, the processing method of True transfer and the simulation method of reflector are my more satisfactory places.
In the process of reflection, there is a more interesting thing. Above: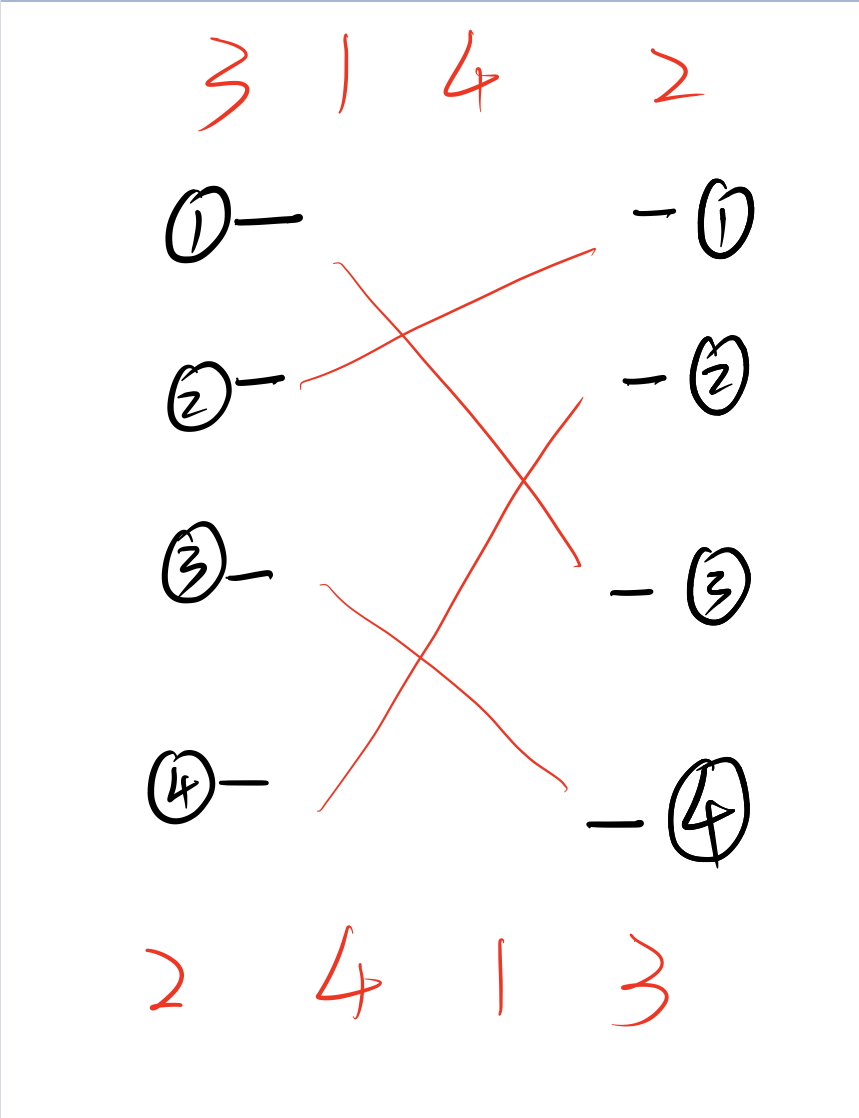
Take four contacts as an example. In forward propagation, we take the left contact as the benchmark and read the serial number of the right contact as 3412. In reverse propagation, we take the right contact as the benchmark and read the serial number of the left contact as 2413. How to build 2413 according to 3412 is a key. A friend of the author provided a good idea. Assuming 3412 is stored in list a, list a is sorted from small to large and stored in list B. Record the subscript of each element in List B in list a in list C, and list C is what we want.
Then follow the example of forward propagation and back propagation.
Let's talk about the use of the code. Create a file named enigma in the same directory of the source code_ code_ book. Txt file, which is used to roughly store the model of Enigma machine, the wiring mode of three runners and one reflector.
Click the operation code and randomly input the Enigma machine batch number composed of three groups of three Arabic numerals, such as 123-456-789. Click enter. At this time, the program will automatically generate the wiring method of this batch number Enigma machine. If this batch of Enigma machine has been used, it shall be used in enigma_ code_ Automatically find the required wiring mode in book.
Then input the initial runner position, which shall be three lowercase English letters separated by commas, such as a, B and C. Press enter, and then enter the plaintext content to be encrypted. Press enter to generate the ciphertext.
If you want to decrypt, you need to enter the same batch number, the same initial rotor position, and enter the ciphertext to decrypt the plaintext.
It should be noted that, following the enigma machine in history, only 26 lowercase English letters are encrypted here, without encryption of numbers, uppercase English letters and punctuation marks. Because these are just some building blocks based on different application requirements. The author also considers that if you want to encrypt Chinese, you can first expand the enigma machine into capital letters and Arabic numerals, and then combine the value of base64.
Let's stop here for the time being. The newcomer writes a blog for the first time. I hope you like it.