Research and reproduction of time A * algorithm based on neural network prediction
1. Thesis reading and information extraction
1.1 construction of road network topology
-
Weighted directed graph
-
The intersection is the vertex of the graph, and the road is the edge of the graph. The topology information needs to be stored:
-
[node type] N represents intersection and R represents road
-
[node index] the index value of each road and intersection vertex
-
[intersection node N]
-
[weight] stores the traffic direction and the corresponding predicted traffic time
-
addNodes add adjacent road node R
-
addInters add adjacent intersection node N and direction——
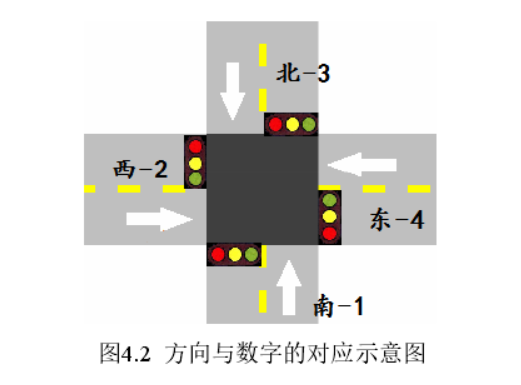
-
-
[road node R]
- [weight] stores the road length
- addNodes add adjacent intersection node N
-
-
This paper gives a simple road network example composed of two-way road R0-R16 and intersection N0-N10
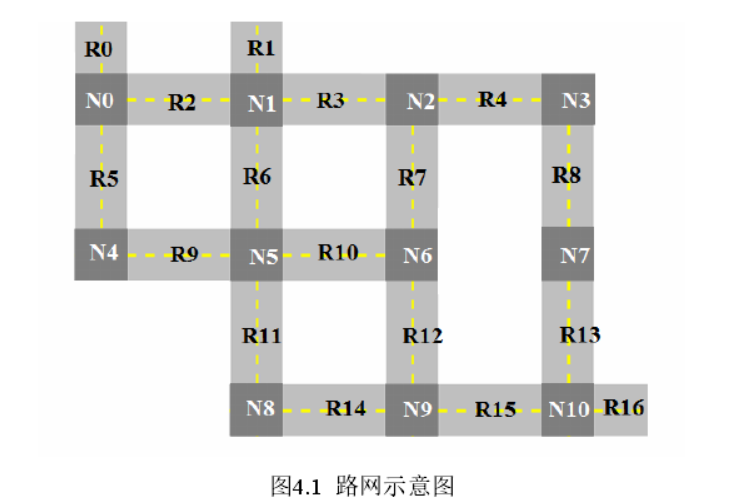
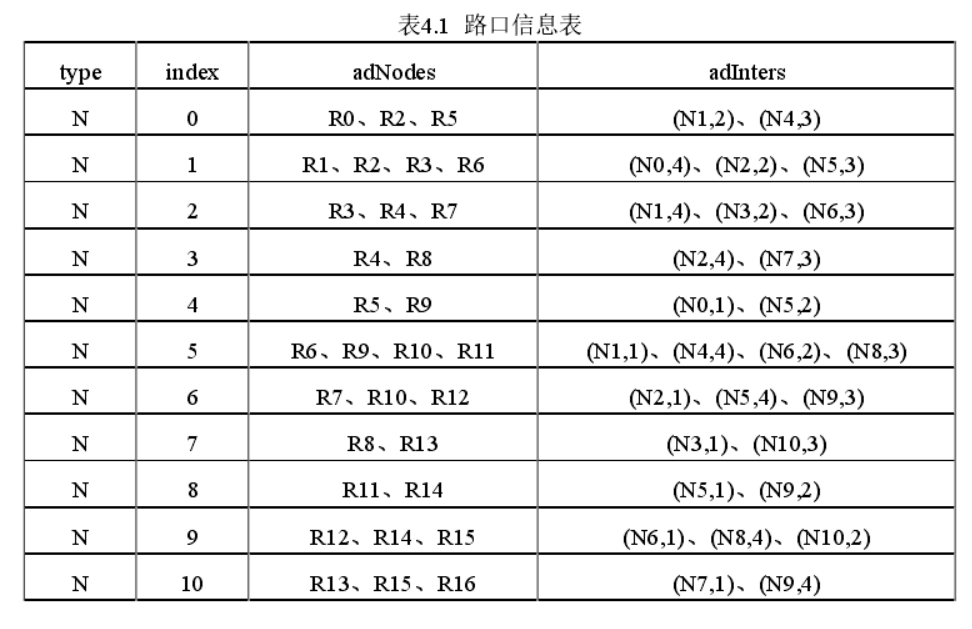
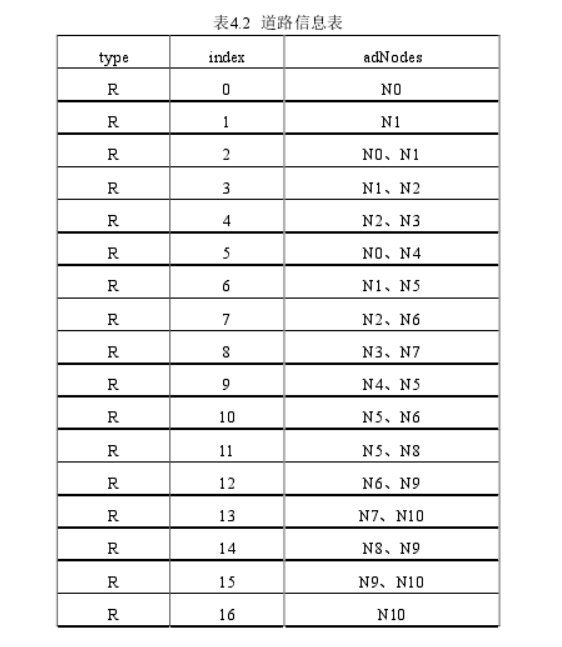
*Parent Node
JAVA implementation in this paper

Python rewrite
class Node():
def __init__(self, type, id, nodes=None, inters=None):
self.type = type
self.id = id
if nodes is None:
self.nodes = []
if inters is None:
self.inters = {}
def addNodes(self, NeighborList):
self.nodes += NeighborList
def addInters(self, TupleList):
for item in TupleList:
self.inters[item[1]] = item[0]
def addNweight(self, dir, weight):
self.Nweight[dir] = weight
def addRweight(self, weight):
self.Rweight = weight
def getID(self):
return self.type + str(self.id)
def getConnections(self):
nodes = []
for i in self.nodes:
nodes.append(i.getID())
if self.type == 'R':
return 'The neighbouring nodes of %s is %s.' % (self.getID(), str(nodes))
if self.type == 'N':
inters = []
for j in self.inters.keys():
inters.append((j, self.inters[j].getID()))
return 'The neighbouring nodes of %s is %s, and neighbouring routes is %s.' % (
self.getID(), str(nodes), str(inters))
def getWeight(self):
if self.type == 'R':
return 'The weight of %s is %s.' % (self.type + str(self.id), str(self.Rweight))
if self.type == 'N':
return 'The weight of %s is %s.' % (self.type + str(self.id), str(self.Nweight))
Variable types in Python
A puzzling problem was encountered when creating the Node class——
In__ init__ When setting the attribute of a class in the function, when the default value of the attribute is variable type, the address of the attribute of all instantiated objects is the same, and the modification of the attribute of an instance object will have a joint reaction to other instance objects. Later, I found that the pit in this is the variable type of python.
-
When is an immutable type

-
When is a variable type

-
resolvent

python's mutable and immutable variables
-
The immutable variable opens up the memory address according to the value, and different variable names with the same value point to the same address; Once the value changes, it will occupy new memory space
x=1 y=1 z=1 print (id(x)) print (id(y)) print (id(z)) #56976040 #56976040 #56976040 x=1 print (id(x)) x+=1 print (id(x)) #52454056 #52454032
-
The address of a variable is opened once it is created, and the same block of memory will not be referenced; For the operation of the same object, the memory address will not change
x=[] y=[] z=[] print (id(x)) print (id(y)) print (id(z)) #62566472 #62669960 #62671368 x=[] print (id(x)) x.append(1) print (id(x)) #49918024 #49918024
-
Therefore, immutable variables are passed by value - different objects with the same value have the same address, and the modified value address changes;
Variable variables are passed by reference - different objects with the same value have different addresses, and the modified value address remains unchanged
-
There are also underlying reasons for all the above... I can't get rid of it. Here's a sentence: everything in Python is an object.
(this reminds me of the JS prototype chain. Is it the same as that all data structures in JS have objects at the top? Come back and compare it after learning it.)
Shared properties in Python
When I first looked for the pit, I was in the wrong direction, so I learned about the problem of shared attributes in python.
Class variables and instance variables in python
- Class variable: a value that can be shared among all instances of a class.
- Instance variable: after instantiation, each instance has its own variable.
- The difference between class variable and instance variable is that class variable is shared by all objects. One object changes its value, and the other objects get the changed result; The instance variable is private to the object. If an object changes its value, it will not affect other objects.
''' Class variable/Class properties 1.In class body(class)Inside, all functions(def)External declaration 2.with<Class name>.<Attribute name>statement Instance variable/Instance properties 1.In class body(class)Inside, all functions(def)Internal declaration to self.<Attribute name>statement '''
1.2 calculation and analysis of driving time (N weight)
The time weight of intersection node can be expressed as:
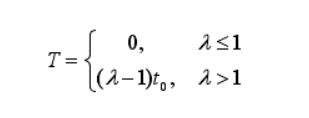
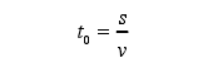
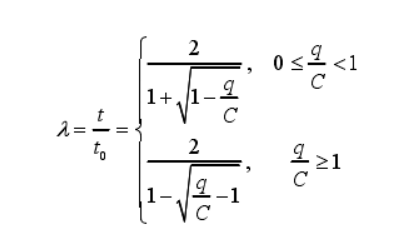
Parameter Description:
- Crossing time T
- Travel time t0 of the road leading to the intersection in case of free flow
- By analyzing a large number of urban traffic flow data, the U.S. highway administration carries out regression analysis to summarize the driving time t of the road section
- Proportional coefficient between actual traffic time and free flow traffic time λ = t/t0
- Traffic flow f
- Capacity of section C
- Blocking rate q/ C
- Length of the road leading to the intersection s
- The driving speed is set as a constant in this paper. It is the maximum speed allowed in urban traffic without congestion. If it is used in the navigation system that can monitor the vehicle speed in real time, it can be set as the vehicle speed v
*Gets the function that calculates the prediction time
Python implementation
def getFlow(t):
pass
def calcTime():
pass
1.3 path planning algorithm A*
algorithm analysis
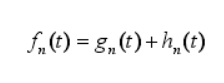
-
Comprehensive cost fn(t):
Value of travel time based cost function of node n
-
Actual cost gn(t):
The travel time from the starting node to node n is calculated according to the stored node time weight information in the process of path search
-
Estimated cost hn(t):
Estimated minimum travel time from node n to target node
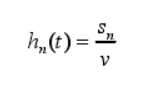
- Manhattan distance sn from node n to target node
- Speed value v set above
Algorithm process
-
Set the start node (N0), target node [N/R] (N9), and departure time t
-
Obtain the predicted travel time of all adjacent intersection nodes of the starting node (N0) at time t, calculate the cost function, and select the best adjacent intersection node for updating
-
Calculate the road travel time to the next node, the sum of the predicted travel time and the node is t1, and the update time is t+t1
-
Obtain the predicted traffic time of all adjacent intersection nodes of the update node at time t+t1, and repeat steps 2-4
-
Target node
-
Target node R:
It is only necessary to judge whether the target node is the adjacent node of the update node after each update of the intersection node. Yes, the search ends.
-
Target node N:
When the target node is reached, the search ends.
-
Algorithm implementation
*Subclass RNode/NNode
class NNode(Node):
def __init__(self, type, id, nodes=None, inters=None, Nweight=None, predictT=None):
super().__init__(type, id, nodes, inters)
self.explored = False
self.time = None
self.F = None
self.G = None
self.H = None
self.father = None
self.direction = None
if Nweight is None:
self.Nweight = {}
if predictT is None:
self.predicT = []
def __str__(self):
return self.getID() + ': ' + self.getConnections() + self.getWeight()
class RNode(Node):
def __init__(self, type, id, nodes=None, Rweight=0, length=0):
super().__init__(type, id, nodes)
self.Rweight = Rweight
self.length = length
*Road network instantiation
This paragraph is really shallow in talent and learning. There is no good way to instantiate in batches. If there is a good method, please don't hesitate to give advice!
nls = []
rls = []
for Nindex in range(11):
nls.append(NNode('N', Nindex))
for Rindex in range(17):
rls.append(RNode('R', Rindex))
nls[0].addNodes([rls[0], rls[2], rls[5]])
nls[1].addNodes([rls[1], rls[2], rls[3], rls[6]])
nls[2].addNodes([rls[3], rls[4], rls[7]])
nls[3].addNodes([rls[4], rls[8]])
nls[4].addNodes([rls[5], rls[9]])
nls[5].addNodes([rls[6], rls[9], rls[10], rls[11]])
nls[6].addNodes([rls[7], rls[10], rls[12]])
nls[7].addNodes([rls[8], rls[13]])
nls[8].addNodes([rls[11], rls[14]])
nls[9].addNodes([rls[12], rls[14], rls[15]])
nls[10].addNodes([rls[13], rls[15], rls[16]])
nls[0].addInters([(nls[1], 2), (nls[4], 3)])
nls[1].addInters([(nls[0], 4), (nls[2], 2), (nls[5], 3)])
nls[2].addInters([(nls[1], 4), (nls[3], 2), (nls[6], 3)])
nls[3].addInters([(nls[2], 4), (nls[7], 3)])
nls[4].addInters([(nls[0], 1), (nls[5], 2)])
nls[5].addInters([(nls[1], 1), (nls[4], 4), (nls[6], 2), (nls[8], 3)])
nls[6].addInters([(nls[2], 1), (nls[5], 4), (nls[9], 3)])
nls[7].addInters([(nls[3], 1), (nls[10], 3)])
nls[8].addInters([(nls[5], 1), (nls[9], 2)])
nls[9].addInters([(nls[6], 1), (nls[8], 4), (nls[10], 2)])
nls[10].addInters([(nls[7], 1), (nls[9], 4)])
rls[0].addNodes([nls[0]])
rls[1].addNodes([nls[1]])
rls[2].addNodes([nls[0], nls[1]])
rls[3].addNodes([nls[1], nls[2]])
rls[4].addNodes([nls[2], nls[3]])
rls[5].addNodes([nls[0], nls[4]])
rls[6].addNodes([nls[1], nls[5]])
rls[7].addNodes([nls[2], nls[6]])
rls[8].addNodes([nls[3], nls[7]])
rls[9].addNodes([nls[4], nls[5]])
rls[10].addNodes([nls[5], nls[6]])
rls[11].addNodes([nls[5], nls[8]])
rls[12].addNodes([nls[6], nls[9]])
rls[13].addNodes([nls[7], nls[10]])
rls[14].addNodes([nls[8], nls[9]])
rls[15].addNodes([nls[9], nls[10]])
rls[16].addNodes([nls[10]])