1, What is joint search set
Joint search set is an algorithm in graph theory
A set is a set, so it can be seen that querying a set is related to the set operation
There are two important operations in the parallel query set: Union and find
The merge operation is used to merge different sets into one set, and the query operation is used to query the set to which an element belongs
2, Take a chestnut
1. Chestnuts
Suppose there are six elements, code 1, 2, 3, 4, 5 and 6
Their set relations are as follows, {1, 2}, {1, 5}, {3, 4}, {6, 2}, which are in the same set in the same curly bracket
Ask if the elements [1, 3] and [2, 5] are in the same set
Idea: connect the elements in the same set according to the set relationship provided. Each set selects a root node as the representative of the set. If the root node of the set where the two elements are located is the same, it means that the two elements are in the same set
Gradually establish their collective relationship as follows
Initially, each element is a collection, and their root node is itself, for example: parent[1] = 1
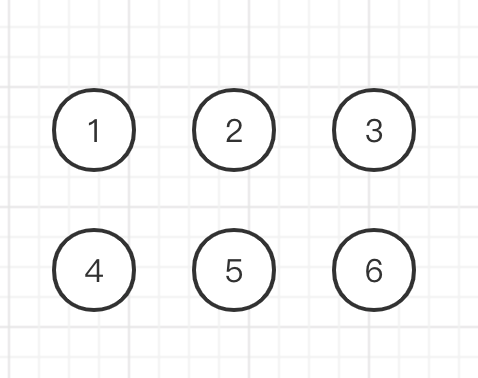
Merge element 1 and element 2. At this time, the root nodes are 1 and 2 respectively. Arbitrarily select element 1 as the root node of the merged set
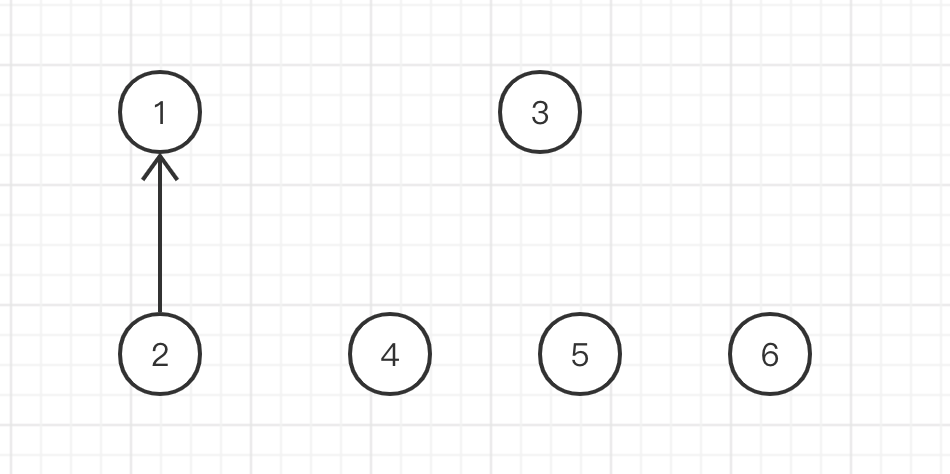
Merge element 5 and element 1 into a set. The root nodes are 1 and 5 respectively. Arbitrarily select element 5 as the root node of the merged set
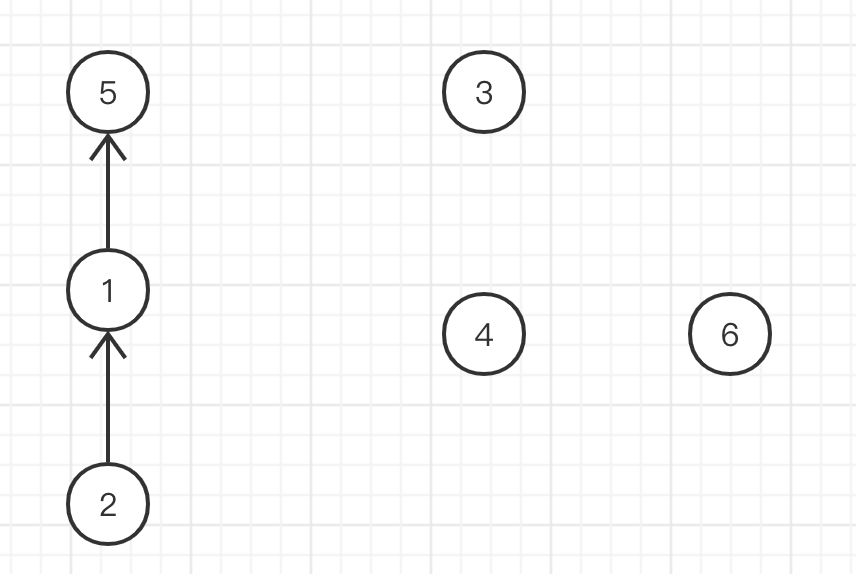
Merge element 3 and element 4. The root nodes are 3 and 4 respectively. Arbitrarily select element 3 as the root node of the merged set
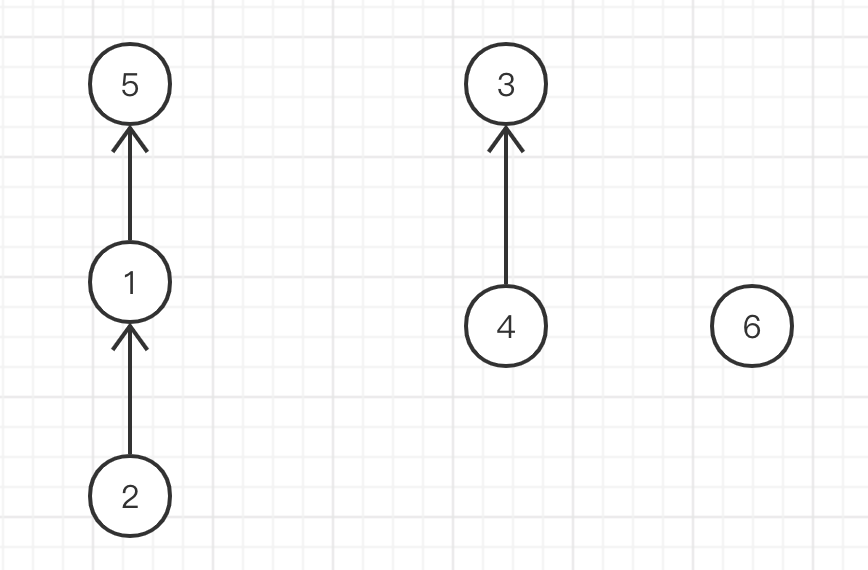
Merge element 2 and element 6. The root nodes are 5 and 6 respectively. Arbitrarily select element 6 as the root node of the merged set
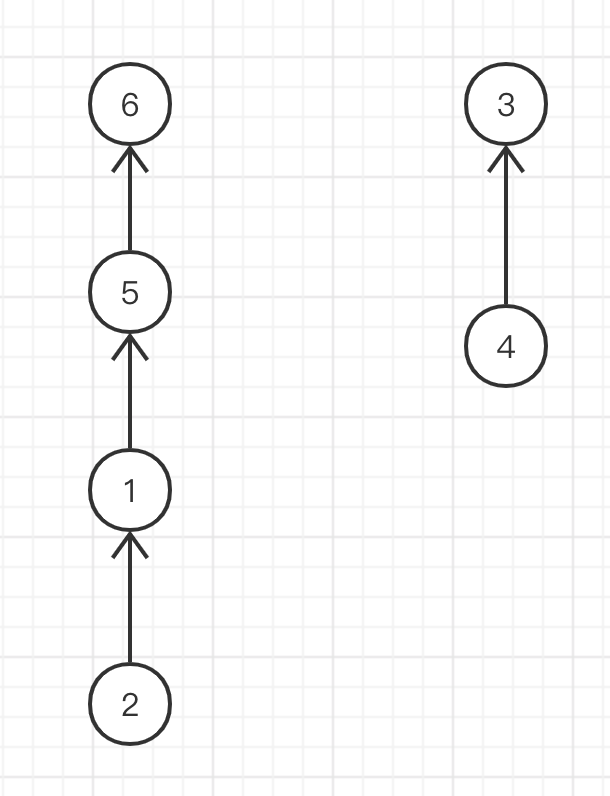
The set relationship is established!
At this time, it starts to judge whether the element belongs to the same set
[1, 3]
The root node of the set where element 1 is located is 6, and the root node of the set where element 3 is located is 3, so they belong to different sets
[2, 5]
The root node of the set where element 5 is located is 6, and the root node of the set where element 2 is located is 6, so they are in the same set
2. Detect the presence of the ring
The union search set can also be used to judge whether there is a ring
For example, we add an association relationship {1, 6} based on the original set
The root node of the set where element 1 is located is 6, and the root node of the set where element 6 is located is also 6. They are in the same set. Therefore, if you continue to add an association relationship, it will lead to the generation of a ring
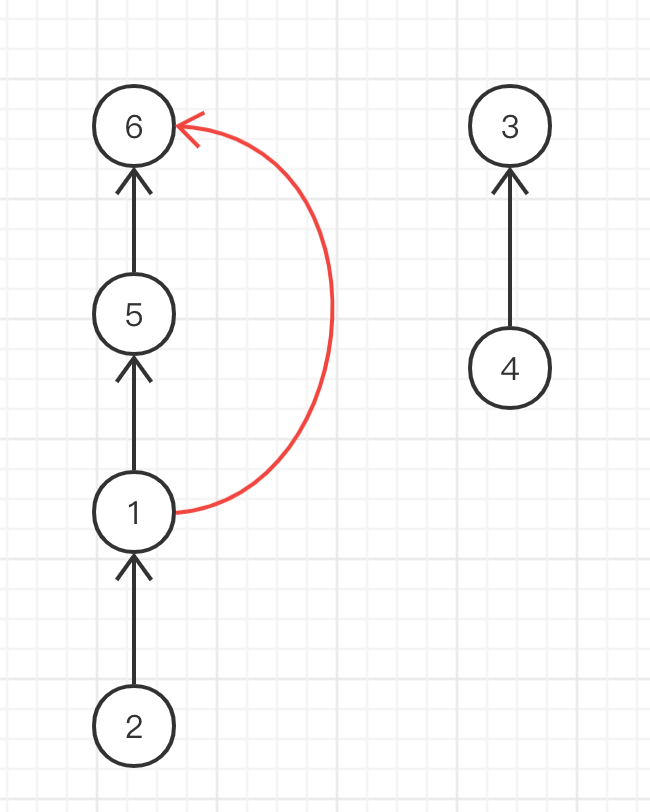
3. Code implementation
Directly implemented with golang
// initialization
func initArray(parent []int) {
for i := 0; i < len(parent); i++ {
parent[i] = -1
}
}
// Find root node
func find(node int, parent []int) int {
if parent[node] == -1 {
return node
}
return find(parent[node], parent)
}
// Merge set
func union(x, y int, parent) bool {
xRoot := find(x, parent)
yRoot := find(y, parent)
if xRoot == yRoot { // The same root node indicates the existence of a ring
return false
}
parent[xRoot] = yRoot
return true
}
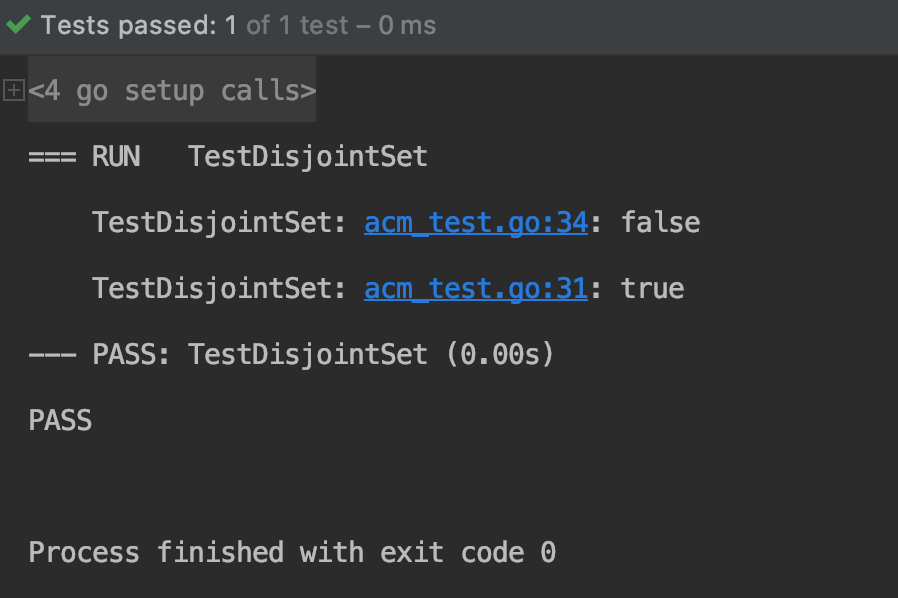
func TestDisjointSet(t *testing.T) {
elementCount, relationCount, questionCount := 6, 4, 2
var relations = [][]int{
{1, 2}, {1, 5}, {3, 4}, {6, 2},
}
var P = [][]int{
{1, 3}, {2, 5},
}
// 1. Initialization
parent := make([]int, elementCount+1)
initArray(parent)
// 2. Merge sets
for i := 0; i < relationCount; i++ {
union(relations[i][0], relations[i][1], parent)
}
// 3. Judge whether it is the same set
for i := 0; i < questionCount; i++ {
aRoot := find(P[i][0], parent)
bRoot := find(P[i][1], parent)
if aRoot == bRoot {
t.Log(true)
continue
}
t.Log(false)
}
}
results of enforcement
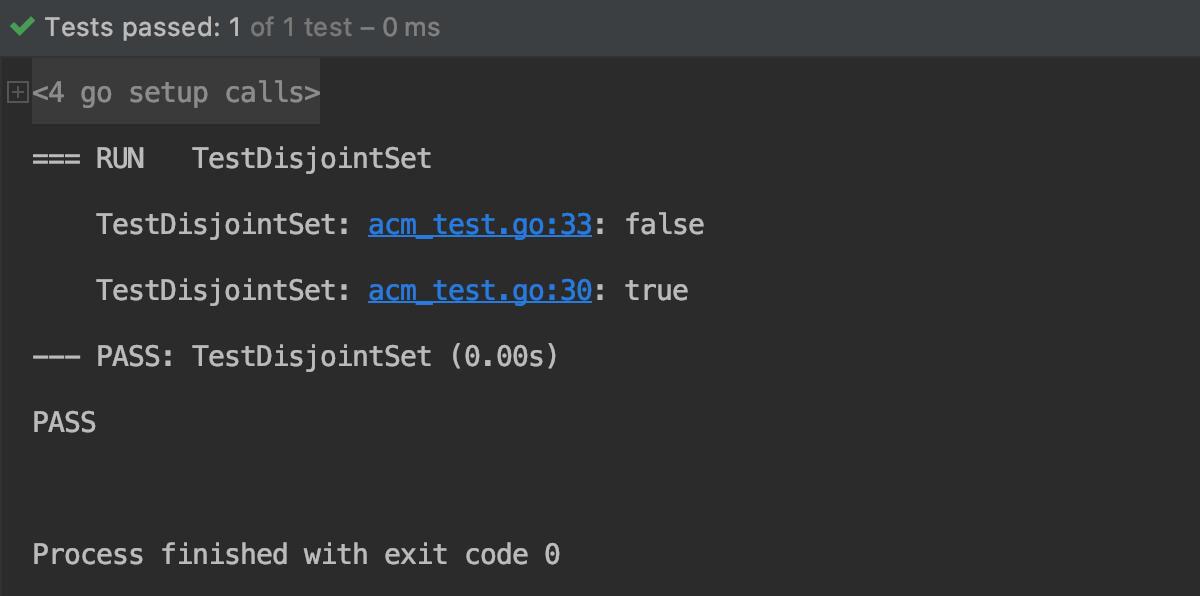
3, Path compression
1. Path optimization
In the above steps, the set on the left needs to traverse the full linked list in extreme cases, so path compression should be considered for optimization
Taking the above elements as an example, the initial state is still six sets, and the association relationships to be established are as follows: {1,2}, {1,5}, {3,4}, {6,2}
Each set is initially assigned a base depth rank of 0 (the initial value assigned here is not important, it is only used for size comparison, as long as the initial value of each element is the same)
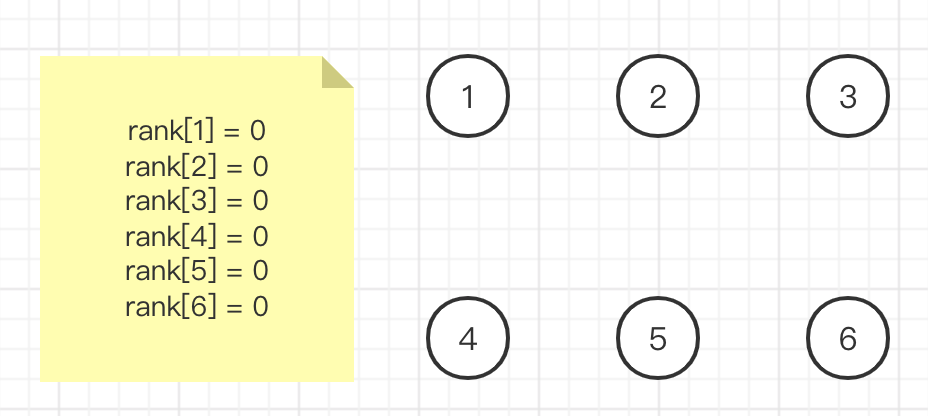
Integrate element 1 and element 2. The root nodes are 1 and 2 respectively. At this time, the number of elements in their collection is equal, so you can specify a root node at will. Here, the rank of the finally selected root node should be increased by one, indicating the increase of tree depth
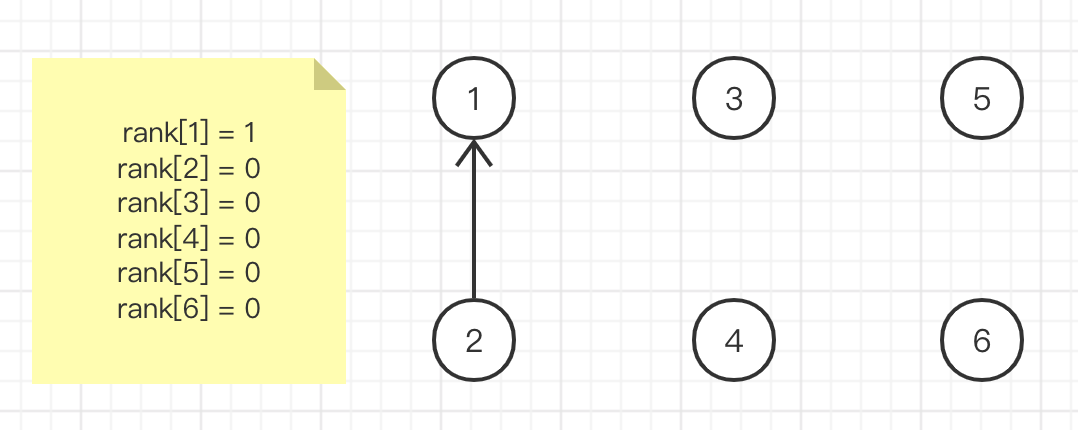
Integrating element 1 and element 5, the root nodes are 1 and 5 respectively, while rank[1] > rank [5]. Therefore, element 1 is selected as the final root node to ensure that the depth of the tree is as small as possible. This is also the purpose of path compression. Here, the depth of the tree does not increase, so rank[1] does not increase automatically
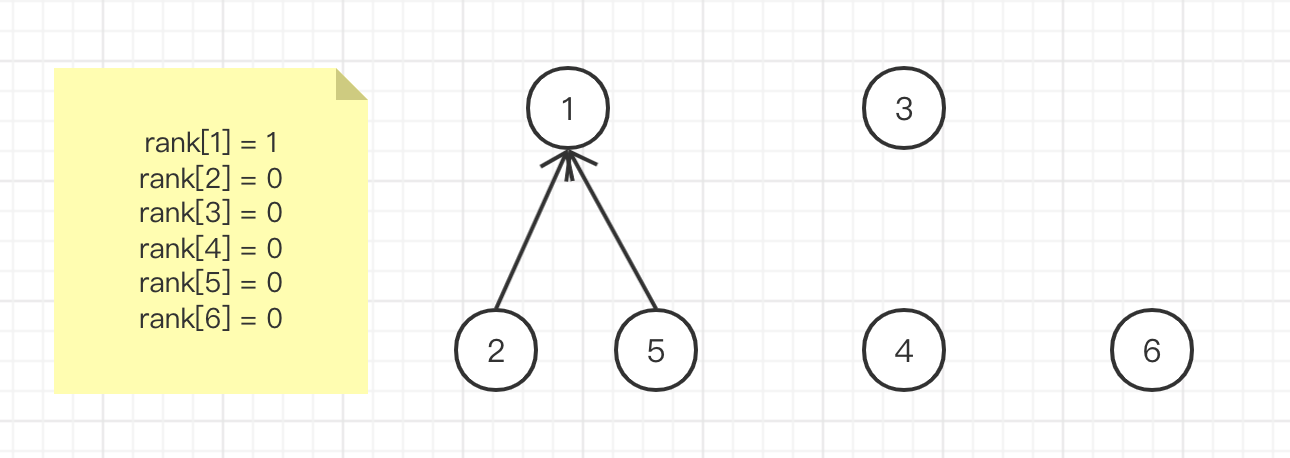
Integrate element 3 and element 4. The root nodes are 3 and 4 respectively. rank[3] == rank[4], so you can select any root node, and rank[root]++
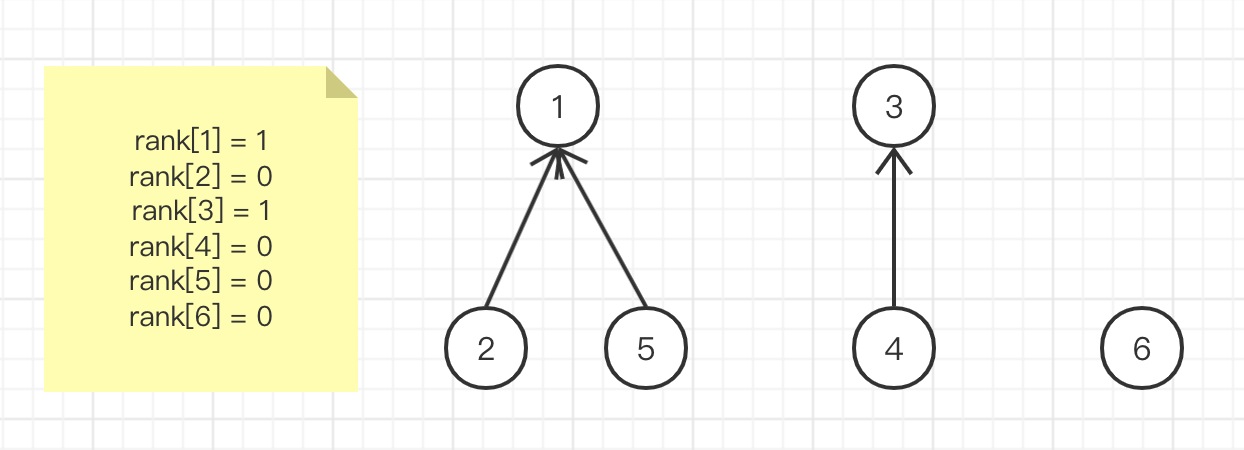
Integrate element 6 and element 2. The root nodes are 1, 6, rank [1] > rank [6], and select element 1 as the final root node
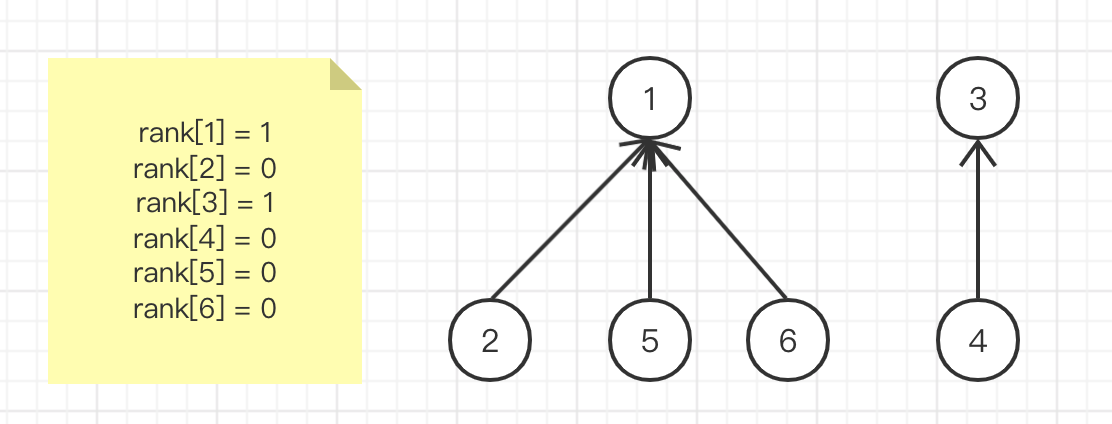
Here, the final spanning tree level is smaller than the upper level and traverses faster. This is path compression, which makes the depth of the spanning tree as small as possible and reduces the nodes to be traversed
The basic idea of path compression is to mount the tree with smaller depth to the tree with larger depth to ensure that the final tree depth is as small as possible
2. Code implementation
// initialization
func initArray(parent, rank []int) {
for i := 0; i < len(parent); i++ {
parent[i] = -1
rank[i] = 0
}
}
// Find root node
func find(node int, parent []int) int {
if parent[node] == -1 {
return node
}
return find(parent[node], parent)
}
// Merge set
func union(x, y int, parent, rank []int) bool {
xRoot := find(x, parent)
yRoot := find(y, parent)
if xRoot == yRoot {
return false
}
if rank[xRoot] > rank[yRoot] {
parent[yRoot] = xRoot
} else if rank[xRoot] < rank[yRoot] {
parent[xRoot] = yRoot
} else {
parent[xRoot] = yRoot // You can choose any node here
rank[yRoot]++
}
return true
}
func TestDisjointSet(t *testing.T) {
elementCount, relationCount, questionCount := 6, 4, 2
var relations = [][]int{
{1, 2}, {1, 5}, {3, 4}, {6, 2},
}
var P = [][]int{
{1, 3}, {2, 5},
}
// 1. Initialization
parent := make([]int, elementCount+1)
rank := make([]int, elementCount+1)
initArray(parent, rank)
// 2. Merge sets
for i := 0; i < relationCount; i++ {
union(relations[i][0], relations[i][1], parent, rank)
}
// 3. Judge whether it is the same set
for i := 0; i < questionCount; i++ {
aRoot := find(P[i][0], parent)
bRoot := find(P[i][1], parent)
if aRoot == bRoot {
t.Log(true)
continue
}
t.Log(false)
}
}
results of enforcement