Title Description
TOM the cat and JERRY the mouse have been competing again recently, but they are adults after all. They don't like to play the game of chasing each other. Now they like to play statistics.
Recently, TOM old cat found something called "reverse order pair" in human class. This thing is defined as follows: for a given sequence of positive integers, the reverse order pair is , a in the sequence_ i>a_ J and I < J. Knowing this concept, they compete who first calculates the number of reverse pairs in a given sequence of positive integers. Note that there may be duplicate numbers in the sequence.
Input format
The first line, a number , n, indicates that there are , n numbers in the sequence.
The second line is n , number, which represents the given sequence. Each number in the sequence does not exceed 10 ^ 9.
Output format
The number of reverse pairs in the output sequence.
Input and output samples
Input
6 5 4 2 6 3 1
Output
11
Description / tips
For 25% data, n ≤ 2500
For 50% of the data, n ≤ 4 × 104.
For all data, n ≤ 5 × one hundred and five
Solution#1 merge sort MergeSort
Explain and guide the principle of merging and sorting Merge sort https://www.iamshuaidi.com/549.html
https://www.iamshuaidi.com/549.html
Why can merge sort be used to find reverse pairs?
- Merge sort uses the idea of divide and conquer. First, the original array is continuously "divided" into "ordered" sequences with only one element, and then the adjacent two arrays are continuously combined, that is, "rule". Then, when any two ordered sequences are combined, When judging the size, just add one more line of code to judge whether the elements in the right array pointed to by index j are smaller than the elements in the left array pointed to by index i. if so, the last element from i to the left array will be larger than the elements pointed to by j, and all elements between i ~ the last element are in reverse order with j, Then add up the numbers between them to be the final answer
- Merge sort is stable, and the position of equal elements will not change
ACCODE
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define maxn 500000+5
int a[maxn], tmp[maxn];
ll cnt;
void merge(int left, int center, int right)
{
int i = left, j = center + 1;
for (int k = left; k <= right; k++)
{
if (i > center)
tmp[k] = a[j++];
else if (j > right)
tmp[k] = a[i++];
else if (a[i] <= a[j])
tmp[k] = a[i++];
else
{
/* Hi!Add the code here!*/
cnt += (center + 1 - i);
tmp[k] = a[j++];
}
}
for (int k = left; k <= right; k++)
a[k] = tmp[k];
}
void mergesort(int left, int right)
{
if (left < right)
{
//center subscript pointing to the last in the left sequence
int center = (left + right) / 2;
mergesort(left, center);
mergesort(center + 1, right);
merge(left, center, right);
}
}
int main()
{
int n;
cin >> n;
for (int i = 0; i < n; i++)
cin >> a[i];
mergesort(0, n - 1);
cout << cnt;
return 0;
}Solution#2; tree array (Binary Indexed Tree)
Supplementary notes:
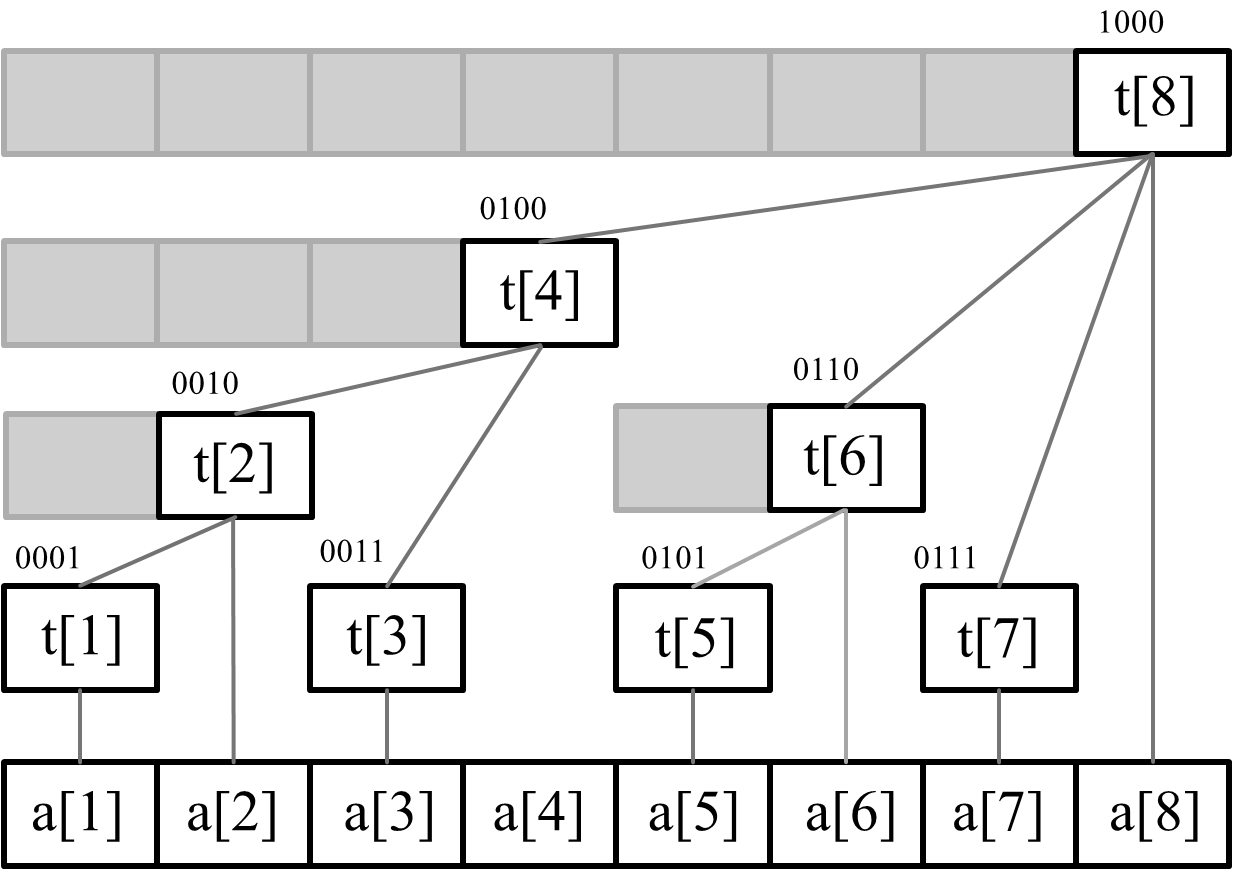
Tree array is an access method realized by binary and lowbit functions to simulate the array into a tree
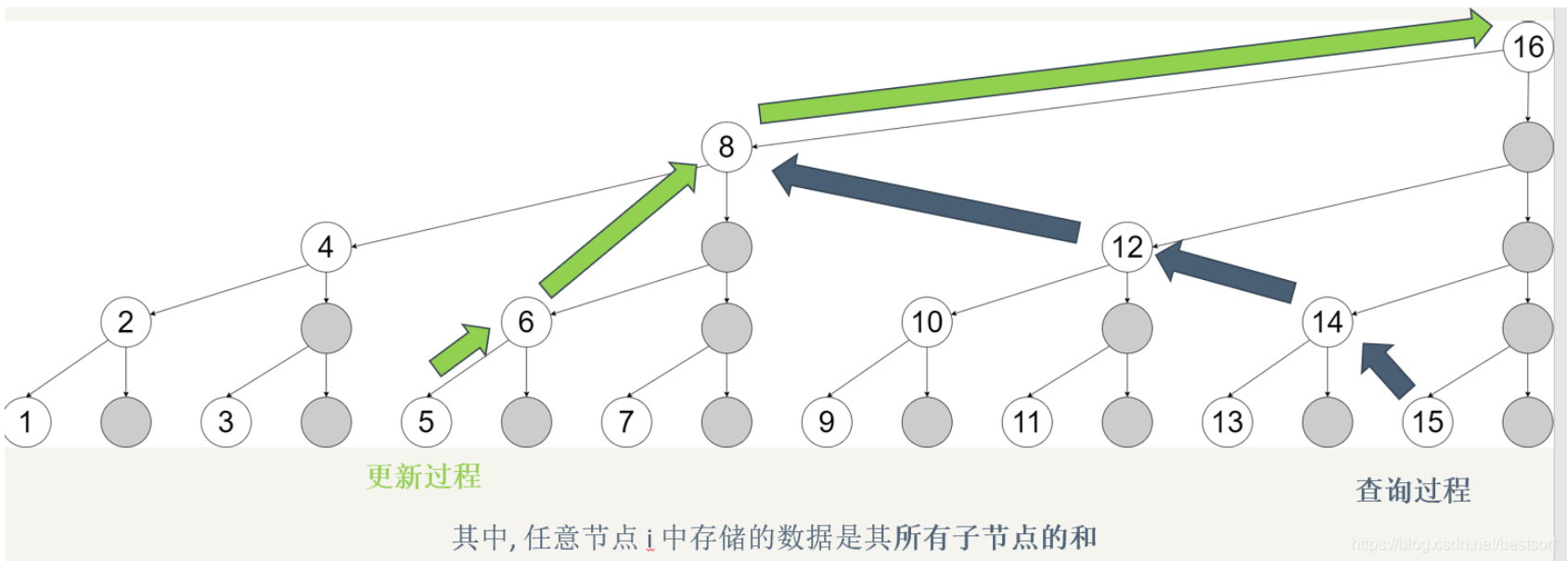
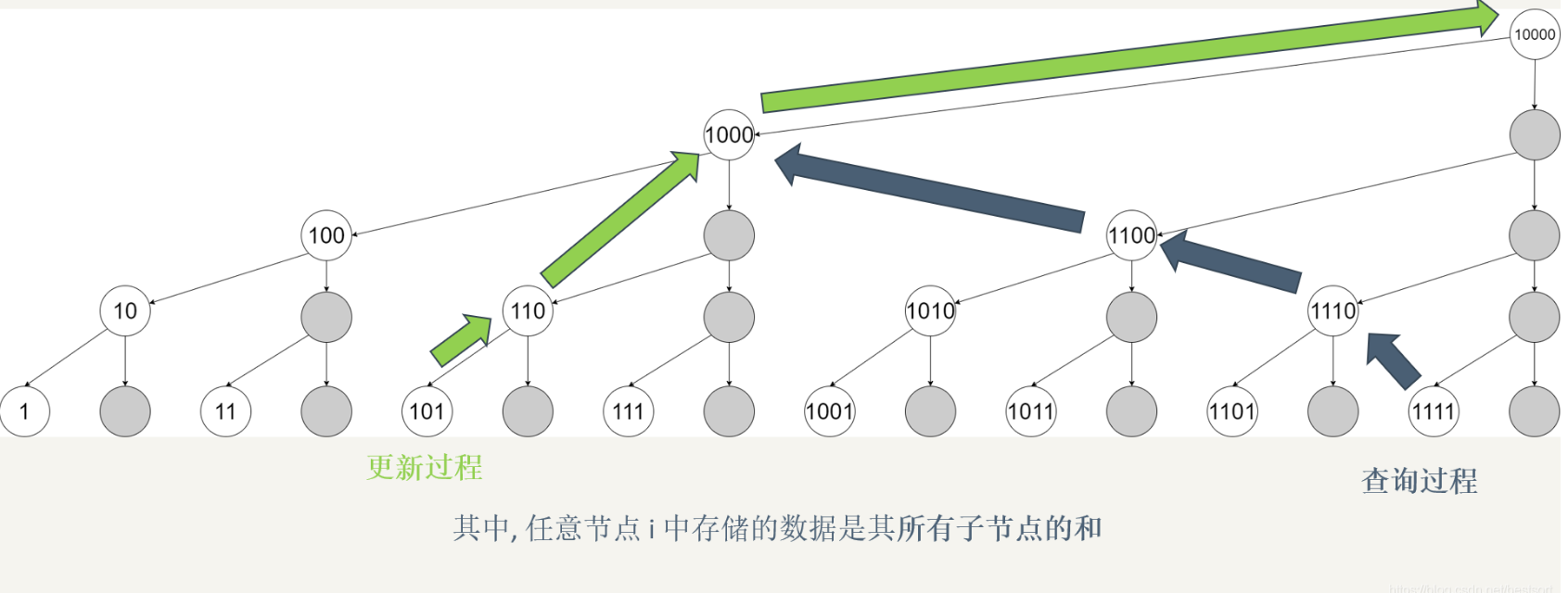
The sum of the values of this node and all its child nodes placed by each node is represented by the tree array. The values obtained from the subscript i+lowbit(i) of each node are its parent nodes (see the link for the principle). In this way, when updating a node, all the parent nodes affecting 1 can be found and updated one by one
For example, if you add 1 to node 5, then tree[5]+1, its parent node = (101 + 1) binary = 110 binary = 6 decimal. Similarly, add 1 to new 110 + 10 = 1000 = 8 nodes, 1000 + 1000 = 10000 = 16 nodes... To maintain interval balance
In query summation, the subscript i-lowbit(i) of each node can get another part of the sum
For example, sum(6) = t[6] + t[4] (t[4] includes t[3]+t[2]+t[1]), while sum(6) = 0b110, 6-lowbit(6) = 0b110 - 0b010 = 0b100 = 4. The obtained 4 is just another part of the sum
Other operations during reverse alignment:
- While storing the original elements with the a array, store the subscript positions of the elements with the p array, and finally sort the p array according to the size of the a array. This is the discretization operation of the original array. For example, the discretized p array of three numbers 110000 and 287777 is {1,3,2,4}, of which 10000 is modified to be 3, It can greatly save the space of tree array (otherwise it will be opened to 87777)
- Start traversing from the first element of the p array. Each element traversed will be at the corresponding position + 1 in the T array. For example, when traversing to 3, t[3]+=1,t[4]+=1, indicating that another element less than or equal to 3 and less than or equal to 4 appears at this time. Start query after updata. If the number less than or equal to 3 is less than 3 at this time, it means that there are still numbers smaller than 3, which is the reverse order pair, The number of reverse pairs of each element is cnt = i - query(i). The difference is that there are several more in the back, which is the reverse pair. Summation is the answer
ACCODE
#include <bits/stdc++.h>
using namespace std;
#define maxn 500000 + 5
typedef long long ll;
int t[maxn], a[maxn], p[maxn];
int n;
ll ans;
int lowbit(int x)
{
return x & (-x);
}
void update(int x)
{
while (x <= n)
{
t[x] += 1;
x += lowbit(x);
}
}
ll query(int x)
{
ll sum = 0;
while (x)
{
sum += t[x];
x -= lowbit(x);
}
return sum;
}
bool cmp(int i, int j)
{
return a[i] < a[j];
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
p[i] = i;
}
stable_sort(p + 1, p + n + 1, cmp);
for (int i = 1; i <= n; i++)
{
update(p[i]);
ans += i - query(p[i]);
}
cout << ans;
return 0;
}