1, Basic concepts

Sequential table is a sequential storage structure of linear table, which uses storage units with continuous addresses to store data elements.

Symbolic representation of sequence table:

Suppose there are n (n ∈ N) data elements of the same type, and the ith element (1 ≤ i ≤ N) is expressed as ai, then the sequence is marked as L={a1, a2,..., ai,..., an}(1 ≤ i ≤ n, n ∈ N)

Graphical representation of sequence table:

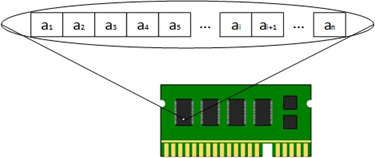
Abstract data type of sequential table:

ADT Sequence table( SqList)
Data
    The data element set of the sequence table is L={a1, a2, ..., ai, ..., an}(1≤i≤n，n∈N)，Each element is of the same type except the first element a1 Other elements have only one precursor element except the last element an Other elements have only one successor element
Operation
    InitList(*L);	# Sequence table initialization
    ListEmpty(L);	# Empty sequence table
    ClearList(L);	# Sequence table empty
    GetElem(L, i, *e);	# Search by bit
    LocateElem(L, e);	# Find by value
    ListInsert(*L, i, e);	# Bitwise insertion
    ListDelete(*L, i, *e);	# Delete by bit
    ListLength(L);	# Returns the length of the sequence table (number of elements)
EndADT

2, Realization idea

The basic idea is very simple. It is to use arrays and pointers to declare the basic structure of the sequence table, and then add, delete, query and modify this basic structure. Note that the addition, deletion, query and modification operation is the basic operation of most data structures, and most functions are composed of these four basic operations. Finally, pay attention to some details, such as basic state judgment, boundary judgment, input filtering, etc., which can effectively improve the robustness of the program.

Divide the operations in the lottery data type into categories according to the basic operations:

Add: InitList(*L), ListInsert(*L, i, e)

Delete: ClearList(L), ListDelete(*L, i, *e)

Query: ListEmpty(L), GetElem(L, i, *e), LocateElem(L, e), ListLength(L)

Change: none. In fact, the "change" operation can be regarded as adding a new value before deleting the old value. Of course, it can be modified directly according to the index in the sequence table

3, Code implementation

1. Basic data structure

(1) State constant

#define OK 1
#define ERROR 0
#define MAXSIZE 20 	/* Initial allocation of storage space*/

(2) Sequential table structure

typedef int Status;
typedef int ElemType;	/*ElemType The type can be determined according to the actual situation*/
typedef struct {
	ElemType data[MAXSIZE];	/*The array stores data elements. The maximum value is MAXSIZE*/
	int length;	/*Record the current length of the sequence table*/
}SqList;

2. Add, delete, modify and query operation prototype

void InitList(SqList *L);	/*Initialize the operation and create an empty sequence table L*/
bool ListEmpty(SqList L);	/*If the sequence table is empty, return true; otherwise, return false*/
void ClearList(SqList *L);	/*Empty sequence table*/
Status ListInsert(SqList *L, int i, ElemType e);	/*Insert element e at position i of the sequence table*/
Status ListDelete(SqList *L, int i, ElemType *e);	/*Delete the element at position i in the sequence table L and return its value with e*/
Status GetElem(SqList L, int i, ElemType *e);	/*Return the value of the ith position element in the sequence table L to e*/
int LocateElem(SqList L, ElemType e);	/*Find the element equal to the given value e in the sequence table. If the search is successful, return the sequence number of the element in the table, indicating success; otherwise, return 0, indicating failure*/
int ListLength(SqList L);	/*Returns the number of elements in the order table L*/
void UnionList(SqList *La, SqList Lb);	/*Merge the two sequential tables and insert all data elements in the sequential table Lb but not in La into la*/

3. Add operation

(1) Sequence table initialization

/*
	Initialization operation, create an empty sequence table L, initialize all its data elements, and set the data length of the sequence table to 0
	@param *L Pointer to sequence table
	@return nothing
*/
void InitList(SqList *L) {
	int i;

	for (i = 0; i < MAXSIZE; i++) {
		L->data[i] = 0;
	}

	L->length = 0;
}

(2) Bitwise insertion

/*
	Insert element. When the sequence table exists, insert element e at the ith position of the sequence table, and add 1 to the data length of the sequence table
	@param *L Pointer to sequence table
	@param i Insert location
	@param e Inserted element
	@return Returns the status of the insertion operation. OK indicates that the insertion is successful, and ERROR indicates that the insertion is wrong
*/
Status ListInsert(SqList *L, int i, ElemType e) {
	int k;

	if (L->length == MAXSIZE) {	/*If the sequence table is full, an error message is returned*/
		return ERROR;
	}

	if (i < 1 || i > L->length + 1) {	/*When the inserted position is not within the range, an error message is returned*/
		return ERROR;
	}

	if (i <= L->length) {	/*When the inserted position is not at the end of the sequence table*/
		for (k = L->length - 1; k >= i - 1; k--) {	/*Move the data elements after the position to be inserted one bit backward in turn*/
			L->data[k + 1] = L->data[k];
		}
	}

	L->data[i - 1] = e;	/*Insert new element*/
	L->length++;

	return OK;
}

4. Delete

(1) Sequence table empty

/*
	Clear the sequence table, delete all data in the sequence table, and set the data length to 0
	@param *L Pointer to sequence table
	@return nothing
*/
void ClearList(SqList *L) {
	int i;

	for (i = 0; i < MAXSIZE; i++) {
		L->data[i] = 0;
	}

	L->length = 0;
}

(2) Delete by bit

/*
	If the sequence table exists, delete the element at the ith position in the sequence table L, and return its value with e, and the length of L is reduced by 1
	@param *L Pointer to sequence table
	@param i Deleted location
	@param *e Pointer to delete element
	@return Returns the status of the deletion operation. OK indicates that the deletion was successful, and ERROR indicates that the deletion was wrong
*/
Status ListDelete(SqList *L, int i, ElemType *e) {
	int k;
	if (L->length == 0) {	/*If the sequence table is empty, an error message is returned*/
		return ERROR;
	}

	if (i < 1 || i > L->length) {
		return ERROR;	/*If the deleted location is incorrect, an error message is returned*/
	}

	*e = L->data[i - 1];	/*Gets the deleted element*/

	if (i < L->length) {	/*If the last position is not deleted*/
		for (k = i; k < L->length; k++) {
			L->data[k - 1] = L->data[k];	/*Moves all elements after the deleted element forward in turn*/
		}
	}

	L->length--;
	return OK;
}

5. Check operation

(1) Empty sequence table

/*
	If the sequence table is empty (i.e. the data length is 0), return true; otherwise, return false
	@param L Initialized sequence table
	@return Returns a Boolean value
*/
bool ListEmpty(SqList L) {
	if (L.length > 0) {
		return false;
	} else {
		return true;
	}
}

(2) Search by bit

/*
	Search by bit and return the i-th position element value in the sequence table L to e
	@param L Initialized sequence table
	@param i Find location
	@param *e Pointer to find element
	@return Returns the status of the search operation. OK indicates that the search is successful, and ERROR indicates that the search is wrong
*/
Status GetElem(SqList L, int i, ElemType *e) {
	if (L.length == 0 || i < 1 || i > L.length) {	/*When the sequence table is empty or the search position is out of range, an error message is returned*/
		return ERROR;
	}

	*e = L.data[i - 1];

	return OK;
}

(3) Find by value

/*
	Find the element equal to the given value e in the sequence table. If the search is successful, return the sequence number of the element in the table, indicating success; otherwise, return 0, indicating failure
	@param L Initialized sequence table
	@param e Elements to find
	@return Find the sequence table position sequence number of elements
*/
int LocateElem(SqList L, ElemType e) {
	if (L.length == 0) {	/*If the sequence table is empty, an error message is returned*/
		return 0;
	}

	int k;
	for (k = 0; k < L.length; k++) {	/*Traverse the sequence table and compare each element value with the given element value*/
		if (L.data[k] == e) {
			return k;
		}
	}

	return 0;
}

(4) Get sequence table length (number of elements)

/*
	Returns the number of elements in the order table L
	@param L Initialized sequence table
	@return Number of current elements in the sequence table
*/
int ListLength(SqList L) {
	return L.length;
}

6. Comprehensive application case of basic operation: consolidation sequence table

/*
	Merge the two sequential tables and insert all data elements in the sequential table Lb but not in La into la
	@param *La	Pointer to linked list a
	@param Lb	Initialized linked list b
*/
void UnionList(SqList *La, SqList Lb) {
	int La_len, Lb_len, i;
	ElemType e;

	La_len = ListLength(*La);
	Lb_len = ListLength(Lb);	/*Gets the length of two sequential tables*/

	for (i = 1; i < Lb_len; i++) {
		GetElem(Lb, i, &e);	/*Take out the ith data element in Lb and assign it to e*/
		if (!LocateElem(*La, e)) {	/*La When the same data element as e does not exist in La, insert the data element into La*/
			ListInsert(La, ++La_len, e);
		}
	}
}

4, Time complexity analysis

Add: if you add an element to the header of the sequence table, all elements after the first element will move backward, and the time complexity is O(n). If you add an element at the end of the table, there will be no elements to move, and the time complexity is O(1). Taken together, the average time complexity is O(n).

Delete: if you delete an element in the header of the sequence table, all elements after the first element must move forward, and the time complexity is O(n). If you delete an element at the end of the table, there are no elements to move, and the time complexity is O(1). Taken together, the average time complexity is O(n).

Query: bit by bit search can directly find the corresponding element according to the index, so the time complexity is O(1); Searching by value requires traversing the sequence table and comparing whether the elements in the sequence table are the same as the given elements one by one. The best case is that the target value is found in the header. At this time, the time complexity is O(1). The worst case is that the target value is found only after traversing the last element at the end of the table. At this time, the time complexity is O(n). To sum up, the average time complexity is O(n).

5, Advantages and disadvantages of sequence table

advantage:

(1) The occupation of space resources is relatively small;

(2) Random access is possible

Disadvantages:

(1) Adding and deleting operations cost a lot of time

(2) The capacity of the sequence table is fixed and cannot be expanded dynamically

(3) Continuous addresses must be used to store data elements, which is easy to cause storage space fragmentation

reference material:

[1] Big talk data structure Cheng Jie

[2] Data structure (C language version). Yan Weimin, WU Weimin