1. Sorting principle

Quick sort is an exchange sort method of binary tree structure proposed by Hoare in 1962. Its basic idea is: any element in the element sequence to be sorted is taken as the reference value, and the set to be sorted is divided into two subsequences according to the sort code. All elements in the left subsequence are less than the reference value, and all elements in the right subsequence are greater than the reference value, Then repeat the process for the leftmost and leftmost subsequences until all elements are arranged in corresponding positions.

1. Sorting main frame

The sorting idea is very simple. The recursive method is used for sorting:

void QuickSort(int* arr,int left,int right){//Quick sort
    if(right-left<2){//Return when the interval value is less than 2
        return;
    }
    int div=PartSort(arr,left,right);//Divide the interval [left, right]
    QuickSort(arr,left,div);//Sort [left,div) intervals
    QuickSort(arr,div+1,right);//Sort the interval div+1 to right
}

The above is the main framework for the implementation of fast sorting recursion. It is found that it is very similar to the pre order traversal rules of binary tree. When writing the recursive framework, you can think about the pre order traversal rules of binary tree and write them quickly. The post order only needs to analyze how to divide the data in the interval according to the benchmark value.

But there are many ways to divide

2. Division method

1. hoare version

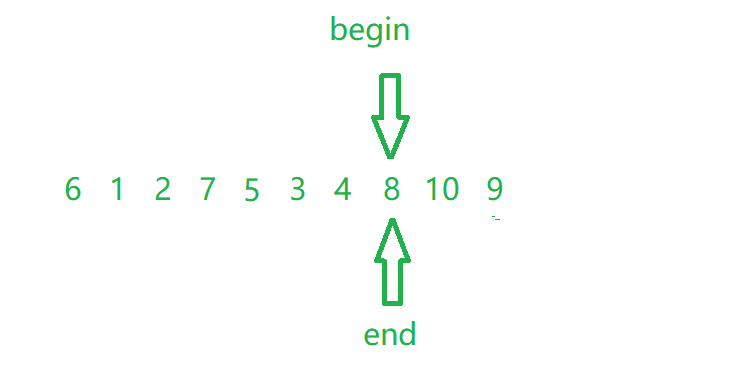
First, we need two pointers: begin points to the beginning and end points to the end. We assume that the benchmark value is end

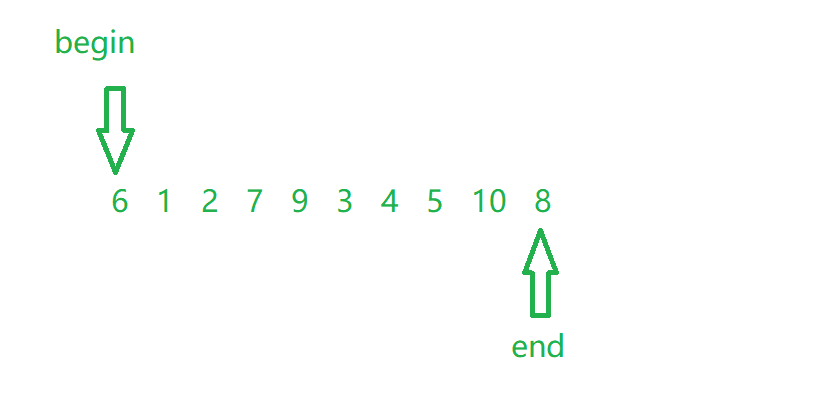
Next, we move the pointer to let begin find the one larger than the benchmark value from front to back, and end find the one smaller than the benchmark value from back to front; After finding, point to the one larger than the reference value and the one smaller than the reference value respectively; Exchange the values they point to when two pointers do not meet; We find that the value of the benchmark has a great influence on the ranking; Next, demonstrate the exchange:

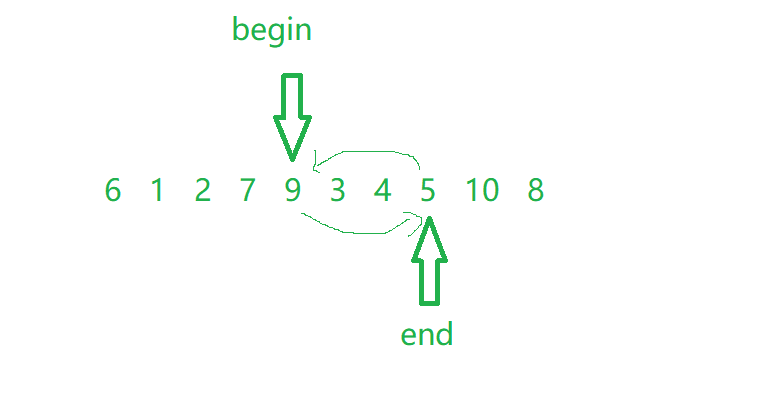
After the exchange, the pointer continues to walk and finds that it meets:

 

If we don't change the benchmark value and the benchmark value on the right, we can't change the benchmark value here:

 

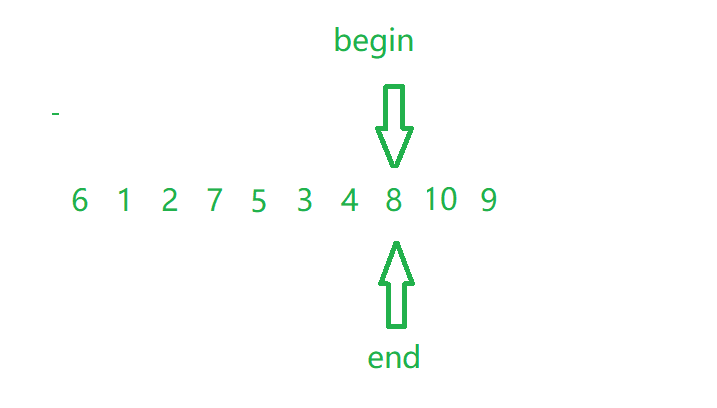
We will find that before 8 is smaller than 8, and after 8 is larger than 8;

be careful!!!! When we change the number, we don't change the benchmark value (8), but if we just want to exchange with the last benchmark value, there will be a bug Therefore, we need to add a judgment statement. The partial code is as follows:

int PartSort2(int* arr,int left,int right){//hoare method
    int begin=left;
    int end=right-1;
    int key=arr[end];
    while(begin<end){
         while(begin<end&&arr[begin]<=key){//begin look from front to back for a value larger than the benchmark value
              begin++;
              }
          while(begin<end&&arr[end]>=key){//end look from front to back for a value smaller than the reference value
              end--;
              }
          if(begin<end){
              Swap(&arr[begin],&arr[end]);//Exchange value
              }
    }
    if(begin!=right-1){//The reference value is not exchanged in the last bit
        Swap(&arr[begin],&arr[right-1]);
    }
    return end;
}

The return value is the new benchmark value. Next, continue recursion  

2. Excavation method

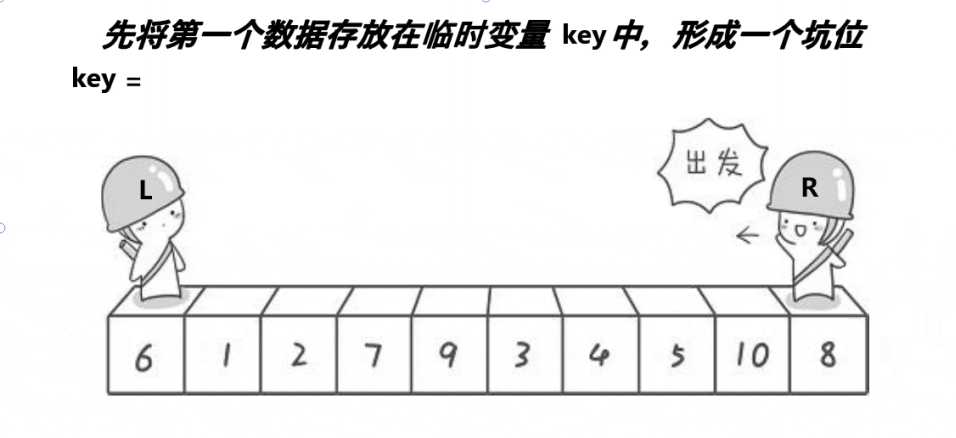
This method is a little similar to the hoare method. We also need two pointers (begin,end); It also points to the front and back positions respectively  

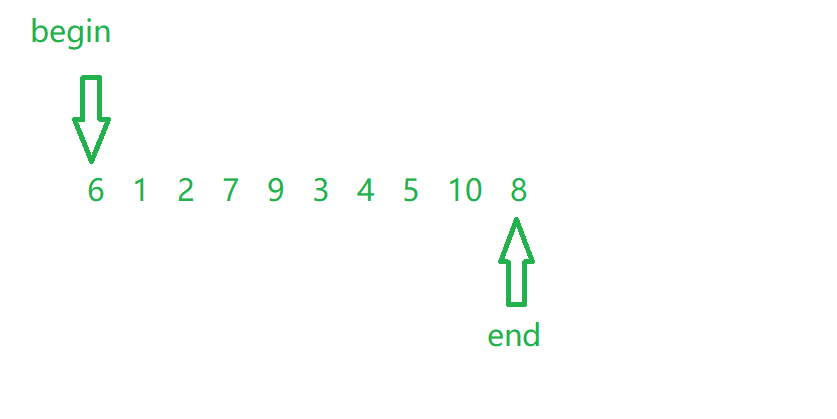
We first save the benchmark value key (also end); When the two pointers do not meet, begin looks for a number larger than key from front to back, and end looks for a value smaller than key from back to front:

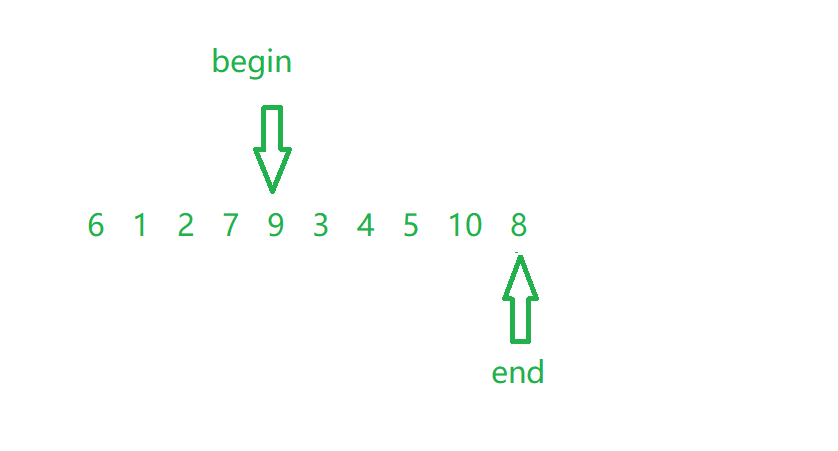
Fill in the end pit with begin (because key=8 has been saved);  

Next, stop at a value smaller than 8 (5);

 

Fill the pit of begin with end (9 has been removed); Then fill in the pit of end with begin, and fill in the pit of begin with end

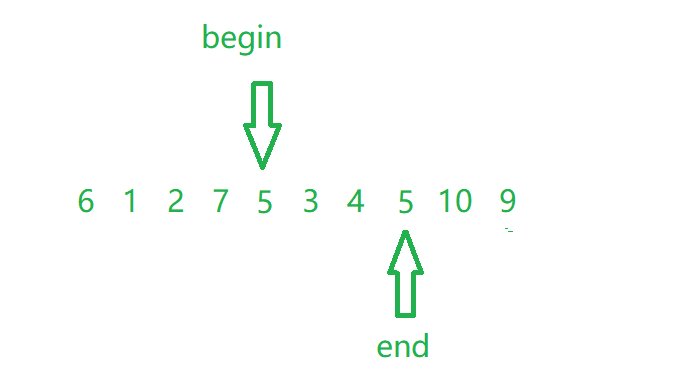When the pointer meets:

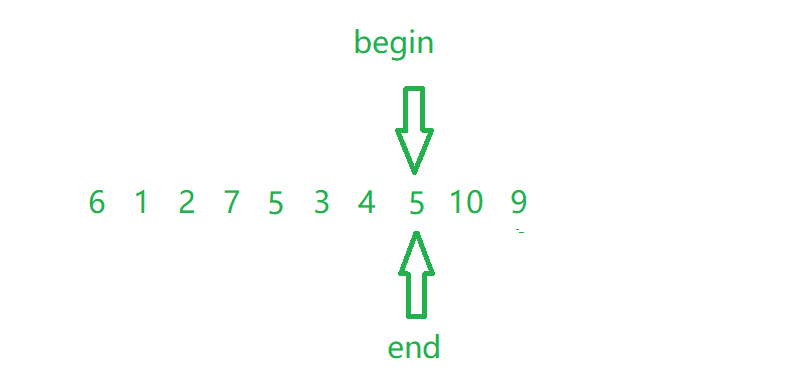
As before, our benchmark value should be 8, and here is 5. Next, we change the benchmark value to 5 (5 already exists);

We will also find that 8 is smaller than 8 before and larger than 8 after 8; The code is as follows:

int PartSort3(int* arr,int left,int right){//Excavation method
    int begin=left;
    int end=right-1;
    int key=arr[end];//Save base value
    while(begin<end){
        while(begin<end&&arr[begin]<=key){//Find a value greater than key from begin and fill in the pit of end
            begin++;
        }
        if(begin!=end){
            arr[end]=arr[begin];
        }
        while(begin<end&&arr[end]>key){//Starting from end, find a value less than begin and fill in the pit of begin
            end--;
        }
        if(begin!=end){
            arr[begin]=arr[end];
        }
    }
    arr[end]=key;
    return end;
}

 3. Front and back pointer method

As before, we also take end as the benchmark value (8); It is also two pointers (cur, prev); Prev = cur-1 (rear pointer); Forward backward linkage traversal

int PartSort1(int* arr,int left,int right){//Front and back pointer method
    int cur=left;//Front pointer
    int prev=cur-1;//Rear pointer
    int key=arr[right-1];//Save base value
    while(cur<right){
        if(arr[cur]<key&&++prev!=cur){
            Swap(&arr[cur],&arr[prev]);
        }
        ++cur;
    }
    if(++prev!=right-1){//Judge whether prev has reached the end. There is no need to exchange at the end
        Swap(&arr[prev],&arr[right-1]);
    }
    return prev;
    }

The picture will not be demonstrated, hahaha! A little fetu

2. Complete sorting code

void Swap(int* a,int* b){
    int tmp=*a;
    *a=*b;
    *b=tmp;
}
int PartSort1(int* arr,int left,int right){//Front and back pointer method
    int cur=left;//Front pointer
    int prev=cur-1;//Rear pointer
    int key=arr[right-1];//Save base value
    while(cur<right){
        if(arr[cur]<key&&++prev!=cur){
            Swap(&arr[cur],&arr[prev]);
        }
        ++cur;
    }
    if(++prev!=right-1){//Judge whether prev has reached the end. There is no need to exchange at the end
        Swap(&arr[prev],&arr[right-1]);
    }
    return prev;
    }
int PartSort2(int* arr,int left,int right){//hoare method
    int begin=left;
    int end=right-1;
    int key=arr[end];
    while(begin<end){
         while(begin<end&&arr[begin]<=key){//begin look from front to back for a value larger than the benchmark value
              begin++;
              }
          while(begin<end&&arr[end]>=key){//end look from front to back for a value smaller than the reference value
              end--;
              }
          if(begin<end){
              Swap(&arr[begin],&arr[end]);//Exchange value
              }
    }
    if(begin!=right-1){//The reference value is not exchanged in the last bit
        Swap(&arr[begin],&arr[right-1]);
    }
    return end;
}
int PartSort3(int* arr,int left,int right){//Excavation method
    int begin=left;
    int end=right-1;
    int key=arr[end];//Save base value
    while(begin<end){
        while(begin<end&&arr[begin]<=key){//Find a value greater than key from begin and fill in the pit of end
            begin++;
        }
        if(begin!=end){
            arr[end]=arr[begin];
        }
        while(begin<end&&arr[end]>key){//Starting from end, find a value less than begin and fill in the pit of begin
            end--;
        }
        if(begin!=end){
            arr[begin]=arr[end];
        }
    }
    arr[end]=key;
    return end;
}
void QuickSort(int* arr,int left,int right){//Quick sort
    if(right-left<2){//Return when the interval value is less than 2
        return;
    }
    int div=PartSort3(arr,left,right);//To divide the interval [left, right], partsort1, 2 and 3 can be selected
    QuickSort(arr,left,div);//Sort [left,div) intervals
    QuickSort(arr,div+1,right);//Sort the interval div+1 to right
}

Give me a compliment~