The work of routing and the role of routing algorithm

• Default router: the host is usually directly connected to a router, which is called the host's default router, also known as the host's first hop router
• Source router: the default router for the source host
• Destination router: the default router for the destination host

• Routing work: the work of routing is to determine the path from the source host to the destination host, which can be summarized as determining the path from the source router to the destination router
• Role of routing algorithm: routing algorithm runs, exchanges and calculates information in network router, and uses this information to configure router forwarding table

Classification of routing algorithms

Centralized global routing algorithm

• Centralized global routing algorithm: by allowing each node to broadcast link state packets to all other nodes in the network (each link state packet includes the characteristics and costs of the link to which it is connected), each node can obtain an equivalent and complete view of the network. Each node can use these complete network information to execute routing algorithm. LS (link state) algorithm is a centralized global routing algorithm.
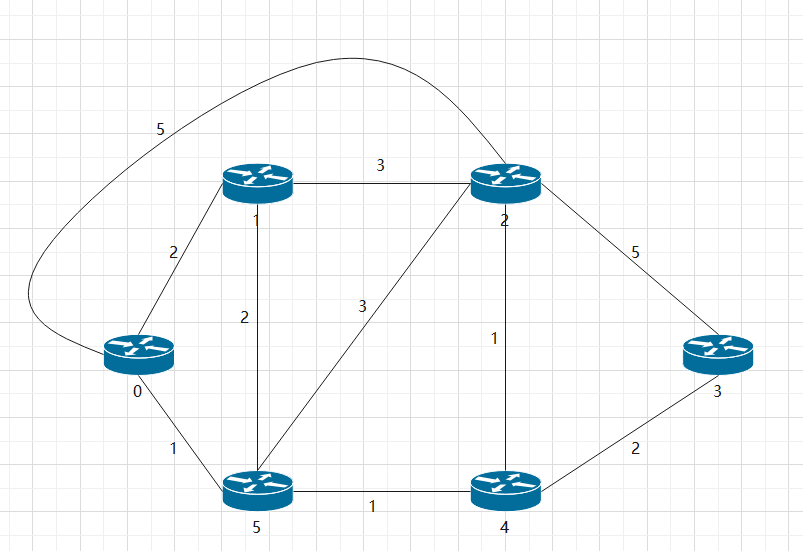
  We use Java to imitate LS algorithm: in the network shown in the figure, router 0 is the source router, and calculate the lowest cost path from the source router to all other routers in the network
  

//LS algorithm implementation
import java.util.ArrayList;

//dists[v].dist: the cost of the lowest cost path from the source router to the destination router V in this iteration of the algorithm
//N ': subset of routers. If the lowest cost path from the source router to a router is known, the router is in set n'
//N: A collection of all routers in the network
class Node{   //Represents a router entity. For the convenience of representation, we do not privatize the member variables of the router entity
    int dist;   //The minimum cost of storing the source router to this router
    boolean ifN;  //ifN is true if the router is included in the set N '(i.e. the lowest cost path from the source router to this router is known)
    ArrayList<Integer> road;  //This list is used to store the intermediate router number from the source router to this router (excluding the source router and this router)
    public Node(int dist,boolean ifN,ArrayList<Integer> road){
        this.dist = dist;
        this.ifN = ifN;
        this.road = road;
    }
}
public class LS{
   public static Node[] LSA(int[][] map){    //The algorithm takes the connectivity between all routers (if not connected, Integer.MAX_VALUE represents ∞) and the cost of all links as the input, and the router array as the return
       Node[] dists = new Node[map.length];//Initializes the length of the array to the number of routers in the network
       for(int i = 0;i < dists.length;i++){
           if(i == 0){
               dists[i] = new Node(0,true,new ArrayList<Integer>());//Initialize the minimum cost of the source router (the source router number is 0) to 0 and ifN to true, because the source router is in the set N 'at the beginning
           }else{
               dists[i] = new Node(Integer.MAX_VALUE,false,new ArrayList<Integer>());//Other routers are not in the set N 'at first, so ifN is initialized to false and the minimum cost is initialized to Integer.MAX_VALUE
           }
       }

       for(int i = 1;i < dists.length;i++){  //Traverse all routers except the source router for initialization
           if(map[0][i] < Integer.MAX_VALUE){   //If this router is connected to the source router, initialize dists[i].dist to map[0][i]
                dists[i].dist = map[0][i];
           }else{                               //If this router is connected to the source router, initialize dists[i].dist to Integer.MAX_VALUE
                dists[i].dist = Integer.MAX_VALUE;
           }
       }
       for(int i = 1;i < dists.length;i++){  //Traverse each router node and calculate the lowest cost and the lowest cost path from the source router to it
           int min = Integer.MAX_VALUE;   //Initializes the minimum value to Integer.MAX_VALUE
           int w = 0; //Used to record routers that are not in N 'and have the smallest dist
           for(int v = 0;v < dists.length;v++){     //Find a router that is not in N 'and has the smallest dist
               if(dists[v].ifN == false && dists[v].dist < min){
                   min = dists[v].dist;
                   w = v;
               }
           }
           if(min < Integer.MAX_VALUE){   //If the source router is disconnected from all other routers in the network, min = integer.max at the first cycle_ Value, overflow occurs in dists[k].dist = dists[w].dist + map[w][k] operation
               dists[w].ifN = true;  //Add router w to set N‘
               dists[w].dist = min;
               for (int k = 0;k < dists.length;k++) {
                   if (dists[k].ifN == false && map[w][k] < Integer.MAX_VALUE && dists[w].dist + map[w][k] < dists[k].dist) {   //map[w][k] < Integer.MAX_ Value also prevents overflow
                       dists[k].dist = dists[w].dist + map[w][k];   //Update the dist of routers connected to router w and not in set N '
                       dists[k].road = (ArrayList<Integer>) dists[w].road.clone();  //Update the intermediate path of router k. The meaning of these two lines of code is that when the conditions in the if statement are met, the intermediate path of router k is the intermediate path of router w, and then add router w
                       dists[k].road.add(w);
                   }
               }
           }
       }
       return dists;   //Return router array
   }
}

//Test LS algorithm
public class Demo {
    public static void main(String[] args) {
        int[][] map = {{0, 2, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 1}, {2, 0, 3, Integer.MAX_VALUE, Integer.MAX_VALUE, 2}, {Integer.MAX_VALUE, 3, 0, 5, 1, 3}, {Integer.MAX_VALUE, Integer.MAX_VALUE, 5, 0, 2, Integer.MAX_VALUE}, {Integer.MAX_VALUE, Integer.MAX_VALUE, 1, 2, 0, 1}, {1, 2, 3, Integer.MAX_VALUE, 1, 0}};
        Node[] dists = LS.LSA(map);
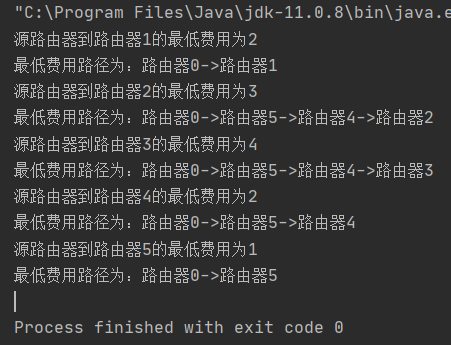
        for (int i = 1; i < dists.length; i++) {
            if (dists[i].ifN == true) {
                System.out.println("Source router to router" + i + "The minimum cost is" + dists[i].dist);
                System.out.print("The lowest cost path is:");
                System.out.print("Router 0->");
                for (int j = 0; j < dists[i].road.size(); j++) {
                    System.out.print("Router"+dists[i].road.get(j)+"->");
                }
                System.out.println("Router"+i);
            }else{
                System.out.println("Router"+i+"Not connected to the source router");
            }
        }
    }
}

test result

Decentralized routing algorithm

• Decentralized routing algorithm: distributed computing, no node has complete information about the cost of all network links, and each node can start working only with the cost knowledge of the links directly connected to it.
• DV (distance vector) algorithm is a decentralized routing algorithm
• Characteristics of DV algorithm
  ① Distributed: each node receives some information from one or more directly connected neighbors, performs calculation, and then distributes its calculation results to neighbors
  ② Iterative: this process continues until there is no more information to be exchanged between neighbors (this algorithm terminates itself, that is, it stops without calculating the signal that should stop)
  ③ Asynchrony: it does not require all nodes to operate in step with each other

Principle of DV algorithm

• Dx(y)=min{c(x,v)+Dv(y)} represents the cost of the lowest cost path from router x to router y
  c(x,v) represents the path cost from router x to its directly connected neighbor router v
  min represents all neighbor routers of router x (i.e. all routers directly connected to router x)
• Dx[Dx(y):y ∈ N] (distance vector) represents the vector of cost estimation from router x to all other routers y in N
  Dx(y) represents the cost of the lowest cost path from router x to router y
  N represents the set of routers in a given network
• In the DV algorithm, for each router x, it needs to maintain the following information
  ①c(x,v)
  ② Distance vector DX of router x [DX (y): y ∈ N]
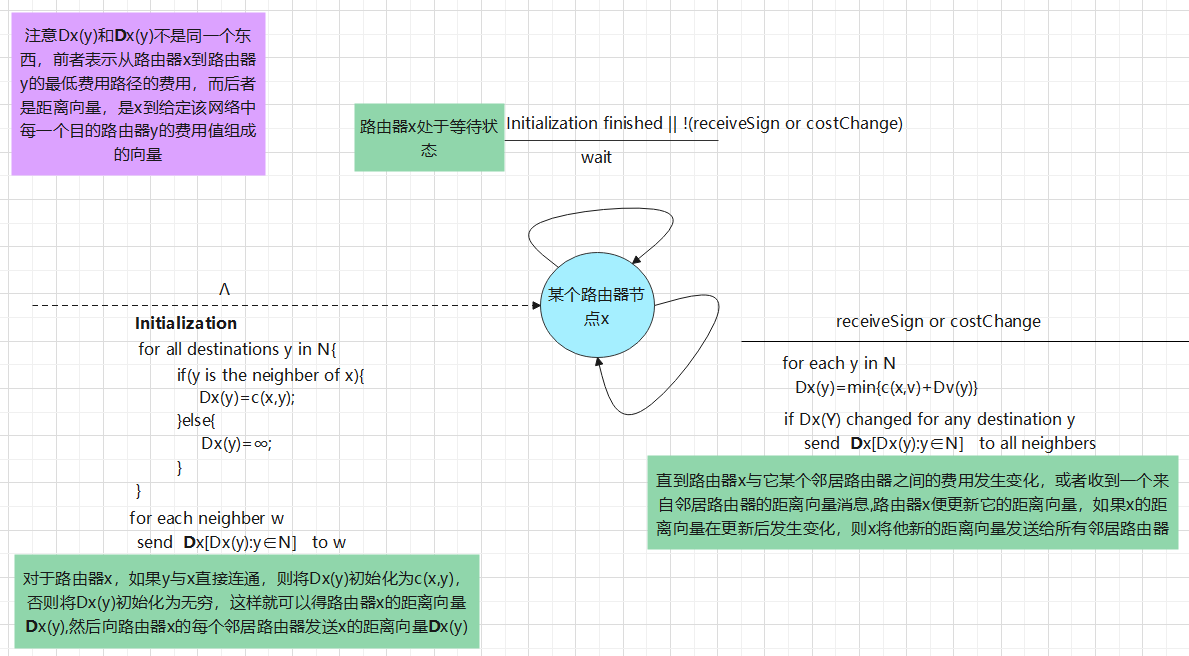
  ③ Distance vector DV of each neighbor v of router x [DV (y): y ∈ N]
• Algorithm flow
  
• We analyze the above algorithm flow with an example
  
  
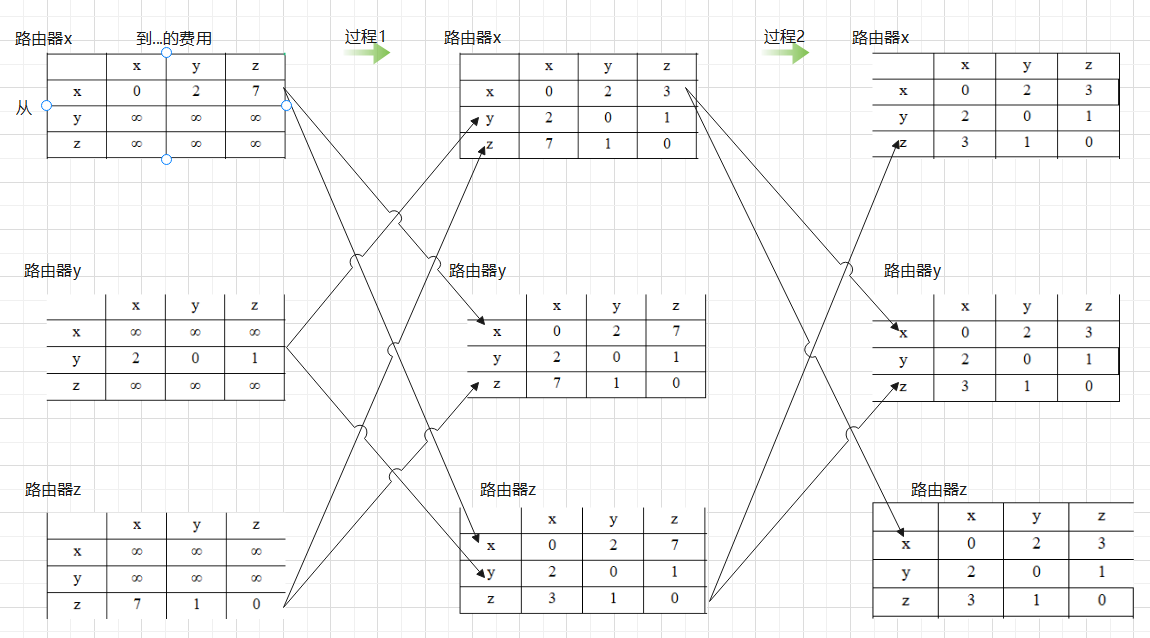
  As can be seen from the algorithm flow chart, in the initialization phase, for router x, if y is directly connected with X, initialize Dx(y) to c(x,y), otherwise initialize Dx(y) to infinity, so as to obtain the distance vector D x(y) of router x, and then send the distance vector D x(y) of X to each neighbor router of router X. therefore, there is the first column and process 1 in the above figure
  As can be seen from the algorithm flow chart, once the cost between router X and one of its neighbor routers changes, or receives a distance vector message from the neighbor router, router x updates its distance vector. If the distance vector of X changes after the update, X sends its new distance vector to all neighbor routers. Therefore, there is the problem in the figure above Column 2 and process 2
  After reaching the third column, after recalculation, the distance vectors of router x, y and z do not change, and the algorithm is in a stable state
• It should be noted that when the cost between the router and one of its neighbor routers changes, or when receiving a distance vector message from the neighbor router, it will update its own vector table. Process 2 in the above figure is due to receiving a distance vector message from the neighbor router, So what happens when the cost between the router and one of its neighbor routers changes? We look at this problem from the two directions of reducing the cost and increasing the cost
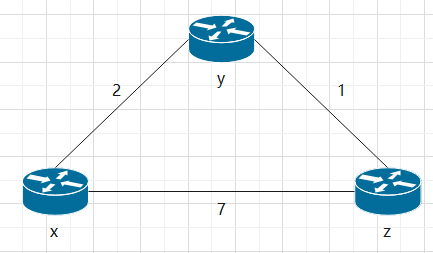
• The cost between the router and one of its neighbor routers becomes smaller (only the relevant entries in the distance table from y and z to destination x are concerned here)
  
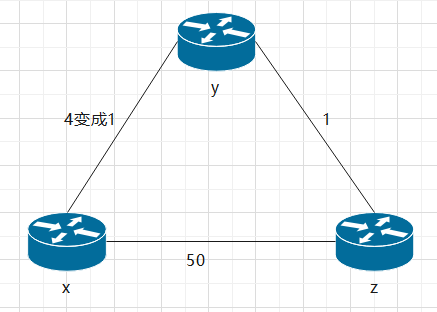
• At time t0, router y detects the change of link cost (the cost changes from 4 to 1), updates its distance vector, and notifies its neighbors of the change
• At time t1, z receives the update message from y and updates its distance table. It calculates the new minimum cost to x (reduced from cost 5 to cost 2), and it sends its new distance vector to its neighbors
• At time t2, y receives an update from z and updates its distance table. The minimum cost of Y remains unchanged, so y does not send any message to z. The algorithm enters a steady state
• When the cost between the router and one of its neighbor routers increases (only the relevant entries in the distance table from y and z to destination x are concerned here)
  
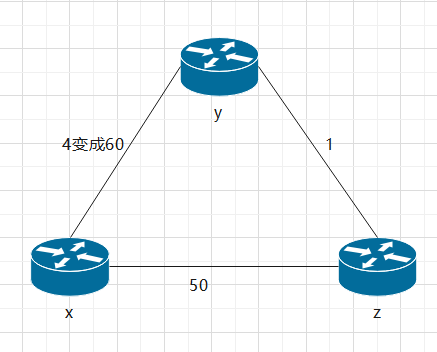
  Before the cost changes, Dy(x)=4,Dy(z)=1,Dz(y)=1,Dz(x)=5;
  After the cost changes, y detects the cost change, starts to update its distance vector Dy(x)=min{c(y,x)+Dx(x),c(y,z)+Dz(x)}=min{60+0,1+5}=6, and notifies Z of the change. If y needs to send a message to x, y will choose to route to X through Z (because in Y's view, the cost of Y - > x is 60, and the cost of Y - > Z - > x is 6). When the message reaches Z, Z will choose to route to X through y (because in Z's view, the cost of Z - > x is 50, and the cost of Z - > y - > x is c(z,y)+Dy(x)=1+6=7). After 44 iterations, Z finds that the cost of Z - > y - > x is greater than 50) After that, Z will send this message directly to X.
  It can be seen that the bad news about the increase of link cost spreads very slowly! This problem is sometimes called the infinite counting problem
• Solution to the infinite count problem: increase toxicity reversal
  The idea is relatively simple: if z is routed to destination X through y, z will announce y, and the distance from z to X is infinite, that is, z will announce Dz(x) = ∞ (z actually knows Dz(x) =5) to y. as long as z is routed to X through y, it will continue to tell y this white lie. Because y believes that z has no path to x, as long as z continues to route to X through y and lies like this), y will never try to route to X through z.
  Loops involving three or more nodes (not just two directly connected neighbor nodes) will not be detected by toxicity reversal technology

Comparison between centralized global routing algorithm and decentralized routing algorithm

• Message complexity. LS algorithm requires each node to know the cost of each link in the network. This requires o (| N | E |) messages to be sent (N represents the number of routers and E represents the number of links), and whenever the cost of a link changes, a new link cost must be sent to all nodes. When the link cost changes, the DV algorithm propagates the changed link cost only when the new link cost changes the lowest cost path of the node connected to the link.
• Convergence speed (the speed at which the algorithm tends to be stable): the time complexity of LS algorithm is O (N) ²) (N indicates the number of routers), while DV algorithm converges slowly and may encounter infinite counting problem
• Robustness: the calculation of LS algorithm is separated to a certain extent, so it provides a certain robustness. In DV algorithm, a node can announce its incorrect lowest cost path to any or all destination nodes

Hierarchical routing

• Why introduce hierarchical routing?
  ① If all routers in the network are treated equally, with the increase of the number of routers, the overhead similar to the change of propagation cost among routers will be very high, resulting in no excess bandwidth to send data packets
  ② An organization should be able to run and manage its network according to its own wishes, and connect its network with other external networks
• These two problems can be solved by organizing routers into autonomous systems (AS)
  Autonomous system internal routing protocol: all routers in the same AS run the same routing algorithm (such AS LS or DV algorithm) and have mutual information. The routing algorithm running in an autonomous system is called autonomous system internal routing protocol
  Gateway router: a router responsible for forwarding packets to destinations other than this AS
  Inter autonomous system routing protocol: obtaining accessibility information from adjacent AS and disseminating accessibility information to all routers in the AS are two tasks handled by inter autonomous system routing protocol