preface
After reading the scan line for a long time, I finally understand it. I want to explain it in my own language to deepen my understanding. Also for readers to learn.
Note: before learning this article, you must first understand the operations such as line segment tree and discretization. Here are two articles b l o g blog blog} for reference: Discretization of programming,Introduction to line segment tree.
Example introduction
-
Title Link
-
General idea of the topic
Here you are n n n) rectangles, find their rectangular area, that is, what is the area covered on the plane.
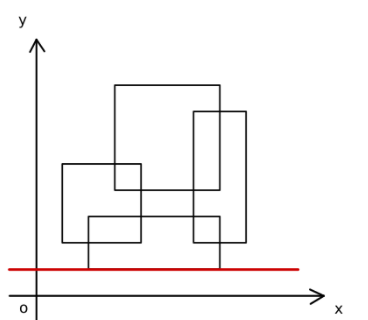
-
reflection
In fact, we can solve the problem of finding the area of each individual rectangle. So for the area where they intersect, we are not only difficult to deal with, but also very error prone, especially when n n n# I can't start when I'm very old. This requires the scan line algorithm we learned in this paper. It can be realized by using line segment tree. It can generally be used to solve the perimeter, volume and area problems of some graphics.
Scan line algorithm
Introduction and demonstration
As the name suggests, we can scan these rectangles with an imaginary scan line, and each time we scan the edge, we can calculate the answer (that is, obtain the area of the block rectangle by the difference between the position scanned to the edge by the last scan line and the width covered). We use the above rectangle to demonstrate:
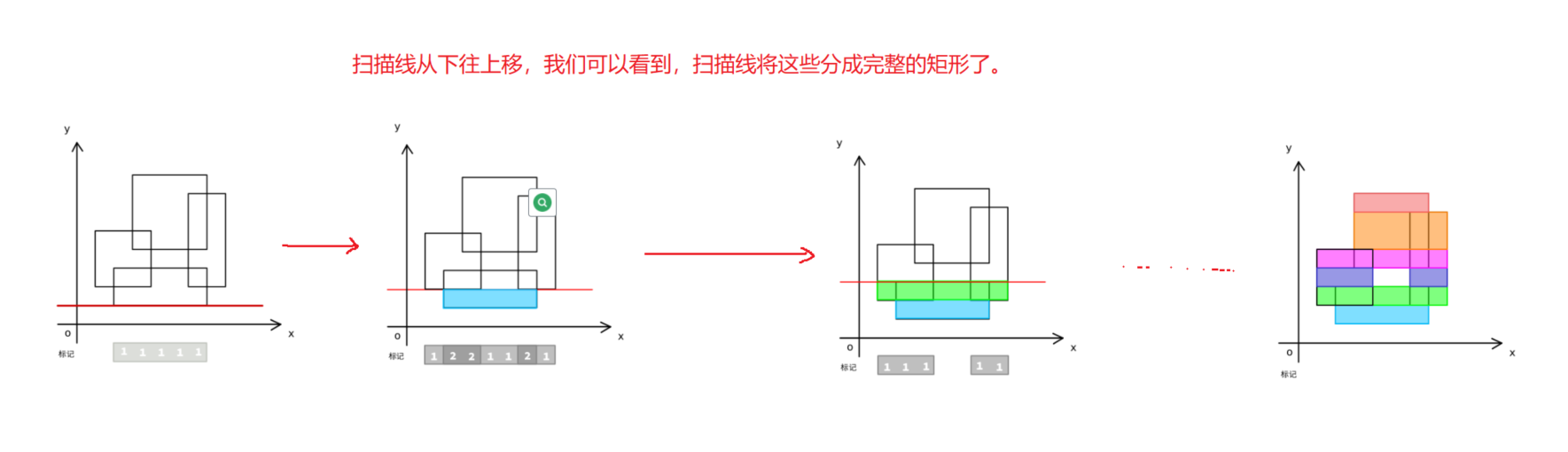
After scanning all the rectangles, we can get the area of the rectangle and.
How
Note: in this article, the scanning line is moved from bottom to top. Of course, it is OK to move from left to right, but the views are different. The code will be given in two copies, from bottom to top and from left to right.
As you can see, we need to know the width and height of the rectangle we divide with scan lines. It can be seen that the height is actually very simple to calculate, that is, the height difference between the current scanning line and the last scanned edge of the scanning line. How to calculate the width? This is also the most difficult point to understand. The concepts of in edge and out edge are introduced here.
In and out edges
We can x x The x # axis is regarded as an interval, i.e [ x l , x r ] [x_l,x_r] [xl, xr] (where x l x_l xl is the leftmost of all rectangles x x x, x r x_r xr is the value at the rightmost end of all rectangles x x x), then it is easy to know that all rectangles are within this interval, and the separation point of this interval is the edge of each rectangle x x x} coordinates.
Then, when we scan with the scan line, we will actually cover a section, and when we encounter = = in edge (bottom edge), we add a rectangle, The coverage area may increase (because the scan line enters the rectangle); when the out edge (top edge) = = is encountered, it indicates that a rectangle is reduced, that is, the coverage area may decrease (because the scan line leaves the rectangle). Then we can calculate the area of the segmented rectangle as long as we calculate the interval length when we encounter the edge. This problem is just realized by using the segment tree.
step
- To convert the in and out edges of a rectangle into scan lines, you need to save the left and right endpoints of the scan lines, i.e x l , x r x_l,x_r xl, xr, so we know the range of the interval. You also need to save the properties of the edge, that is, whether it is an out edge or an in edge + + +Operation, edge out − - − operation, so we can make 1 1 1 is the inlet side, − 1 -1 − 1 − is the edge; Then you need to save the height of the edge, that is, the height of the two scan lines is the height of the divided rectangle.
- The scan lines are sorted by height. Because we have to traverse from bottom to top, it is naturally sorted by height.
- Establish a segment tree to maintain the coverage interval length, so we still need to use it at this time c o v e r cover cover array to count the number of interval coverage, using a l e n g t h length The length array counts the interval length of nodes.
Interval indicates precautions
-
Because our nodes save intervals, and because the left and right endpoints of intervals can be floating-point, if we deal with them in this way, there will be errors, and because the interval length is essentially unevenly distributed, which is not in line with the assumption of our segment tree, we need to disperse the intervals, that is, we can save all the interval endpoints first, and then sort them through u n i q u e unique The unique} function is used to remove duplicates, so that each endpoint can be represented by their sequence number. Then, query their interval and find the sequence number by binary value. This saves space and is easy to operate.
-
Since our segment tree maintains the length of the segment rather than the value of the point, we need to pay attention to the interval of the left child when dividing the left and right children. The right endpoint is equal to the left endpoint of the right child. Only in this way can there be no gap in interval segmentation.
code implementation
- Sweep from bottom to top
/**
*@filename:new_Rectangular area and
*@author: pursuit
*@created: 2021-08-08 14:58
**/
#include <bits/stdc++.h>
#define debug(a) cout << "debug : " << (#a)<< " = " << a << endl;
#define x first
#define y second
using namespace std;
typedef pair<double,double> pdd;
typedef long long ll;
const int N = 4e5 + 10;
const int P = 1e9 + 7;
const int INF = 0x3f3f3f3f;
struct Line{
double xl,xr;//The left and right ends of the scan line.
double yy;//The height of the scan line.
int d;//Represents whether the edge is in or out, in which the bottom edge is in and the top edge is out.
bool operator < (const Line &A){
return yy < A.yy;
}
Line(){}
Line(double _xl,double _xr,double _yy,int _d):xl(_xl),xr(_xr),yy(_yy),d(_d){}
}scan[N];
int cover[N];//Coverage of interval i.
double length[N];//Length of endpoint i.
double xx[N];//Store the discretized x value.
int n,k,tot;//n rectangles. tot scan lines.
void pushup(int rt,int l,int r){
//Judge whether the interval is completely covered.
if(cover[rt]){
//Update interval length.
length[rt] = xx[r] - xx[l];
}
else if(l + 1 == r){
//Because cover[0] = 0 and is a leaf node. The leaf node cannot be covered by the contribution of child nodes.
length[rt] = 0;
}
else{
length[rt] = length[rt << 1] + length[rt << 1 | 1];
}
}
void update(int rt,int l,int r,int xl,int xr,int d){
//Judge whether the interval of the current node is completely covered
if(xl <= l && xr >= r){
//Just update this interval.
cover[rt] += d;//Update the coverage of this interval.
pushup(rt,l,r);
return;
}
if(l + 1 == r)return;
int mid = (l + r) >> 1;
if(xl <= mid){
update(rt << 1,l,mid,xl,xr,d);
}
if(xr > mid){
update(rt << 1 | 1,mid,r,xl,xr,d);
}
pushup(rt,l,r);
}
void solve(){
//Sort scanlines and x.
sort(xx + 1,xx + tot + 1);
sort(scan + 1,scan + tot + 1);
//Get the length after weight removal. It also discretizes xx.
int len = unique(xx + 1,xx + tot + 1) - (xx + 1);
//initialization.
fill(cover,cover + N,0);
fill(length,length + N,0);
int xl,xr;//Get xl and xr after discretization.
double ans = 0;
for(int i = 1; i <= tot; ++ i){
//The height difference between two adjacent scan lines is high. length[1] represents the coverage width of the interval governed by the root node, which is the width.
ans += length[1] * (scan[i].yy - scan[i - 1].yy);
//Add this scanline to the segment tree.
//Find the first element greater than or equal to the search value. Because the duplicate is removed and must exist, it is its own subscript.
xl = lower_bound(xx + 1,xx + len + 1,scan[i].xl) - xx;
xr = lower_bound(xx + 1,xx + len + 1,scan[i].xr) - xx;
update(1,1,len,xl,xr,scan[i].d);
}
printf("Test case #%d\nTotal explored area: %.2f\n\n",k,ans);
}
int main(){
k = 0;
pdd a,b;
while(~scanf("%d", &n) && n){
k ++,tot = 0;
for(int i = 1; i <= n; ++ i){
scanf("%lf%lf%lf%lf", &a.x, &a.y, &b.x, &b.y);
scan[++tot] = Line(a.x,b.x,a.y,1);
xx[tot] = a.x;
scan[++tot] = Line(a.x,b.x,b.y,-1);
xx[tot] = b.x;
}
solve();
}
return 0;
}
- Sweep from left to right
/**
*@filename:Rectangular area and
*@author: pursuit
*@created: 2021-08-07 20:33
**/
#include <bits/stdc++.h>
#define debug(a) cout << "debug : " << (#a)<< " = " << a << endl;
#define x first
#define y second
using namespace std;
typedef pair<double,double> pdd;
typedef long long ll;
const int N = 4e5 + 10;
const int P = 1e9 + 7;
const int INF = 0x3f3f3f3f;
int n,k;
struct Line{
double yd,yu,xx;//The y-up coordinate, y-down coordinate and abscissa of the edge.
int d;//Distinguish between in and out edges. The in side is 1 and the out side is - 1
bool operator < (const Line &A){
return xx < A.xx;
}
Line(){}
Line(double _yd,double _yu,double _xx,int _d):
yd(_yd),yu(_yu),xx(_xx),d(_d){}
}scan[N];//Scan line.
int tot;//Number of scan lines.
int cover[N];//Store the corresponding coverage value of i node.
double length[N];//Total length under storage section i.
double yy[N];//Store the value of y after discretization. We use lower as the subscript_ Bound to find.
void pushup(int rt,int l,int r){
if(cover[rt]){
length[rt] = yy[r] - yy[l];
}
else if(l + 1 == r){
length[rt] = 0;//To the leaf node.
}
else{
length[rt] = length[rt << 1] + length[rt << 1 | 1];
}
}
void update(int rt,int l,int r,int yl,int yr,int d){
if(yl <= l && yr >= r){
//Note that all sections are included.
cover[rt] += d;//Add the corresponding value according to the out edge and in edge.
pushup(rt,l,r);
return;
}
if(l + 1 == r)return;//Child node reached.
int mid = (l + r) >> 1;
if(yl <= mid){
update(rt << 1,l,mid,yl,yr,d);
}
if(yr > mid){
update(rt << 1 | 1,mid,r,yl,yr,d);
}
pushup(rt,l,r);
}
void solve(){
sort(yy + 1,yy + tot + 1);//Sort.
sort(scan + 1,scan + 1 + tot);
//Get the array after de duplication.
int len = unique(yy + 1,yy + tot + 1) - (yy + 1);
fill(length,length + N,0);
fill(cover,cover + N,0);
int yl,yr;
double ans = 0;//Accumulate the rectangular area.
for(int i = 1; i <= tot; ++ i){
ans += length[1] * (scan[i].xx - scan[i - 1].xx);
yl = lower_bound(yy + 1,yy + 1 + len,scan[i].yd) - yy;
yr = lower_bound(yy + 1,yy + 1 + len,scan[i].yu) - yy;
update(1,1,len,yl,yr,scan[i].d);
}
printf("Test case #%d\nTotal explored area: %.2f\n\n",k,ans);
}
int main(){
pdd a,b;
while(~scanf("%d", &n) && n){
k ++;
tot = 0;
for(int i = 0; i < n; ++ i){
//Coordinates of the lower left and upper right corners of the rectangle.
scanf("%lf%lf%lf%lf", &a.x, &a.y, &b.x, &b.y);
//Lower bottom scan line and upper bottom scan line.
//That is, assign values to the in and out edges.
scan[++tot] = Line(a.y,b.y,a.x,1);
yy[tot] = a.y;
scan[++tot] = Line(a.y,b.y,b.x,-1);
yy[tot] = b.y;
}
solve();
}
return 0;
}