E - Charles in Charge

Topic meaning: a person riding on the road with a battery car can be charged at every point. You can run as many miles as there is electricity. Now you are required to run the distance. The smaller the battery capacity of the electric vehicle, the better. What is the minimum capacity of the electric vehicle.
Idea: first run the shortest circuit to find the normal shortest circuit, and then calculate the battery capacity of the tram, that is, the length of the road. When dealing with the shortest circuit, the road larger than the battery capacity should be deleted, but it is difficult to operate, so it is directly in D i j k s t r a Dijkstra In Dijkstra, roads with a capacity greater than the battery capacity are not operated directly, which can be regarded as having no such side.

#include <bits/stdc++.h>
using namespace std;
#define inf 0x7f7f7f7f3f3f3f3f
#define int long long
const int N = 1e4 + 10, M = 2e5 + 10;
typedef pair<int, int> PII;
#define ll long long
bool vis[N];
int dis[N];
int h[N], w[M], e[M], ne[M], idx;
int n, m, x;
ll dex;
void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

int dijkstra(int mid) {
    memset(dis, 0x7f, sizeof(dis));
    memset(vis, 0, sizeof(vis));
    dis[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII> > q;
    q.push({0, 1});
    while (q.size()) {
        auto t = q.top();
        q.pop();
        int now = t.second;
        int distance = t.first;
        if (vis[now]) continue;
        vis[now] = 1;
        for (int i = h[now]; i != -1; i = ne[i]) {
            int j = e[i];
            if (w[i] > mid) {
                continue;
            }
            if (dis[j] > dis[now] + w[i]) {
                dis[j] = dis[now] + w[i];
                q.push({dis[j], j});
            }
        }
    }
    return dis[n];
}
signed main() {
    memset(h, -1, sizeof(h));
    cin >> n >> m >> x;
    while (m--) {
        int a, b, c;
        scanf("%lld%lld%lld", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }
    dex = (ll)dijkstra(inf);
    dex = dex + dex * x / 100;
    int l = 0, r = dex + 1;
    while (l < r) {
        int mid = (l + r) / 2;
        if ((ll)dijkstra(mid) <= dex) {
            r = mid;
        } else {
            l = mid + 1;
        }
    }
    cout << l << endl;
}

D - Bridge Automation

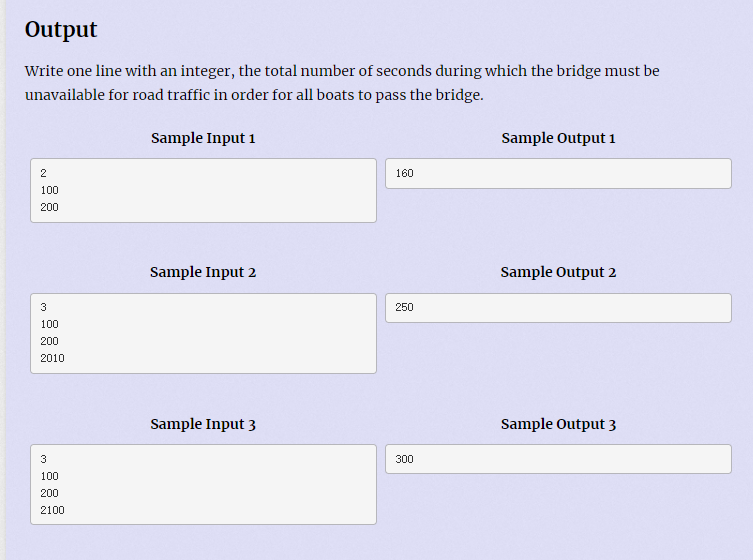
Meaning: it takes 60 seconds for a bridge to rise and fall. It takes 20 seconds for a ship to cross the bridge. A ship can wait in front of the bridge for up to 30 minutes. The ship can pass only when it is fully raised. If there are multiple ships waiting in front of the bridge, it also needs to pass one by one. Now give the arrival time of each ship, Now ask how long you should keep lifting at least (the process of lifting and lowering also counts)
Idea: establish f ( i ) f(i) f(i) is to i i The time when the bridge remains raised until i ships.
I The first i − 1 i-1 i − 1 didn't wait for it, No i i When i ship arrives, the whole process of raising, lowering and crossing the bridge is completed, that is f ( i − 1 ) + 60 + 60 + 20 f(i-1)+60+60+20 f(i−1)+60+60+20
II There is a ship waiting for it in front, and the ship waiting for it is ship j. then there are two situations at this time
1. Ship j couldn't wait. After waiting for 30 minutes, she drove away. For 30 minutes, the bridge was fully lowered, but the bridge remained fully raised, so it was f [ j − 1 ] + a [ i ] − a [ j ] − 1800 + 20 + 120 f[j-1]+a[i]-a[j]-1800+20+120 f[j−1]+a[i]−a[j]−1800+20+120
2. If ship j can wait, it will wait for ship i, that is f [ j − 1 ] + ( i − j + 1 ) ⋅ 20 + 120 f[j-1]+(i-j+1)·20+120 f[j−1]+(i−j+1)⋅20+120

#include <bits/stdc++.h>
using namespace std;
const int N = 4444;
int a[N], f[N];
int n;
int main() {
    ios_base::sync_with_stdio(false);
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    for (int i = 1; i <= n; i++) {
        f[i] = f[i - 1] + 140;
        for (int j = 1; j < i; j++) {
            f[i] = min(f[i], f[j - 1] + max((a[i] - a[j] - 1800) + 20 + 120, (i - j + 1) * 20 + 120));
        }
    }
    cout << f[n] << endl;
    return 0;
}

J - Programming Tutors

Meaning: give the plane coordinates of n students and N coaches. The distance between them is Manhattan distance, so that the students and coaches can match each other, so that the maximum distance between them can be minimized
Idea: dichotomy + Hungary, dichotomy: the maximum matching distance between them. If it is less than the correct answer res, it must not be matched in pairs. If it is greater than, it must be matched in pairs, but the distance can be narrowed. When matching in the bipartite graph, mid is used as the boundary. If the distance is greater than mid, both sides cannot match. Finally, see whether they can match one by one.

#include <bits/stdc++.h>
using namespace std;
const int N = 222;
#define ll long long
struct node {
    ll x, y;
} a[N], b[N];
ll g[N][N];
int vis[N];
int match[N];
int n;
bool find(int u, ll mid) {
    for (int i = 0; i < n; i++) {
        if (g[u][i] <= mid && !vis[i]) {
            vis[i] = 1;
            if (match[i] == -1 || find(match[i], mid)) {
                match[i] = u;
                return 1;
            }
        }
    }
    return 0;
}
bool check(ll mid) {
    int res = 0;
    for (int i = 0; i < n; i++) {
        memset(vis, 0, sizeof(vis));
        if (find(i, mid)) res++;
    }
    if (res == n)
        return 1;
    else
        return 0;
}
int main() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> a[i].x >> a[i].y;
    }
    for (int i = 0; i < n; i++) {
        cin >> b[i].x >> b[i].y;
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            g[i][j] = abs(a[i].x - b[j].x) + abs(a[i].y - b[j].y);
        }
    }
    ll l = 0, r = 1e12;
    while (l < r) {
        memset(match, -1, sizeof(match));
        ll mid = (l + r) / 2;
        if (check(mid))
            r = mid;
        else
            l = mid + 1;
    }
    cout << l << endl;
    return 0;
}

To be continued
If you have any suggestions or criticisms and additions, please leave a message and point it out. Thank you very much