Greatest common divisor

1. Seeking the Maximum Common Number
Euclidean algorithm-rolling Division
(a, b) maximum common divisor gcd(a, b) minimum common divisor lcm(a, b)
Theoretical basis: gcd(a, b) = gcd(b, a mod b)

//Core Code
int gcd(int a, int b)
{	
	return b > 0 ? gcd(b, a % b) : a;
}

AcWing 1246. Equal difference series

The math teacher gave Xiao Ming a question about summing up the equal difference columns.

But careless Xiao Ming forgot part of the columns and only remembered N integers.

Now given these N integers, Xiao Ming wants to know how many items are in the shortest column of equal difference that contains these N integers?

Input Format
The first line of input contains an integer N.

The second line contains N integers A1,A2,, AN. (Note that A1_AN is not necessarily an equal difference
Order in column given)

Output Format
Output an integer to represent the answer.

Data Range
2≤N≤100000,
0≤Ai≤109
Input sample:
5
2 6 4 10 20
Output sample:
10
Sample Interpretation
The shortest isometric column containing 2, 6, 4, 10, 20 is 2, 4, 6, 8, 10, 12, 14, 16, 18, 20.

thinking

Equal difference series: a1, a1 + d, a1 + 2d,..., a1 + nd;
Find out what the maximum tolerance is,

Code

import java.util.*;

public class Main {
    static final int N = 100010;
    static int n;
    static int[] a = new int[N];
    
    static int gcd(int a, int b) {
        return b > 0 ? gcd(b, a % b) : a;
    }
    
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        for (int i = 0; i < n; i ++ ) {
            a[i] = in.nextInt();
        }
        Arrays.sort(a, 0, n);
        int d = 0;
        for (int i = 1; i < n; i ++ ) {
            d = gcd(d, a[i] - a[0]);
        }
        
        if (d == 0) System.out.print(n);
        else {
            n = (a[n - 1] - a[0]) / d + 1;
            System.out.print(n);
        }
    }
}

Basic Theorems of Arithmetic

Prime factor decomposition:

AcWing 1295. Factor Chain of X

Enter a positive integer X to find the maximum length of a strictly increasing sequence whose factor X is greater than 1 that can divide any of the preceding items, and the number of sequences that satisfy the maximum length.

Input Format
The input contains multiple sets of data, one row for each set, and a positive integer for X.

Output Format
For each set of data, the maximum length of the output sequence and the number of sequences that meet the maximum length.

Each result takes one line.

Data Range
1≤X≤220
Input sample:
2
3
4
10
100
Output sample:
1 1
1 1
2 1
2 2
4 6

thinking

Similar to equal ratio columns: a1, a2, a3,..., an;
Set the prime factor to pi,
a1, a1 * p1, a1 * p1 * p2, ... , a1* p1* ... * pn

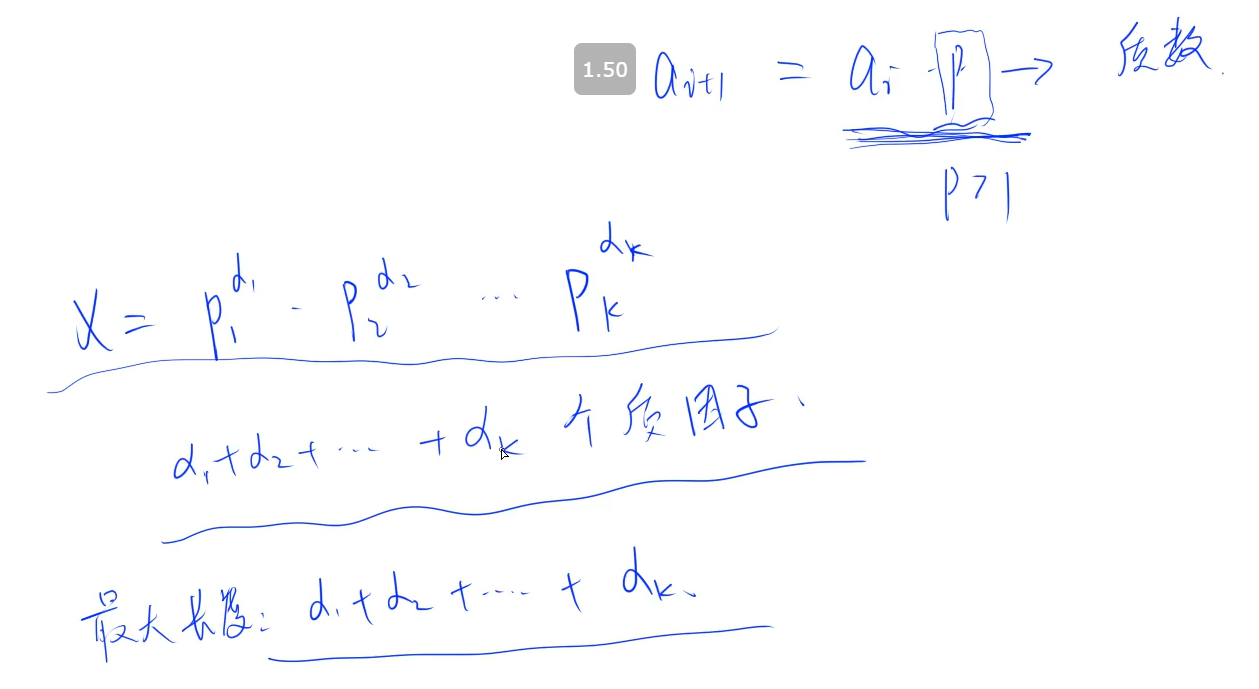
For example, 22 X 33 X 5,
There are 6! Species arrangement
But some of them are duplicated, for example, 2 has two, the positions of these two numbers can be exchanged, so we put the same group into one group, and then each class has a common: 2! X 3! 6!/ 2! X3! Classes

How do you understand that?
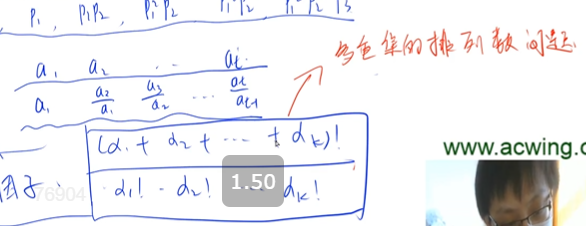
For the original sequence a1, a2, a3,..., an
There is a sequence similar to the differential sequence (temporarily referred to as the division fraction group): a1, a2/a1, a3/a1,..., an/an-1, each number of which corresponds to the prime factor of X; In order to ensure that the latter item divides any of the previous items, so each subsequent item must be multiplied by all the items in front of it, so that both the divisible and the increasing sequence are guaranteed. Then our longest sequence is equal to the sum of prime factors. How can we find how many different sequences satisfy the longest sequence? Changing from a division group to an original array, such as item 2 a2/a1, to A2 requires multiplying by a1, so for these division groups, the latter one will be an-1 times larger than the previous one, regardless of how their positions are swapped, so the longest sequence we need to differ is to divide the full arrangement of the groups, taking care to weigh them down. For instance:
For number 10:
It has three factors 2, 5, 10, of which there are two prime factors, and then we arrange the prime factors
2， 5
5， 2
The above sequences belong to division sequence (division group)
To return to the original number is listed as:
2, 2 * 5(10)
5, 5 * 2 (10)
So the answer is:
The longest sequence is: 2;
There are two longest sequences.

Directly decomposing the prime factor can be very large and difficult to decompose
Knowledge Points:
Screening for prime numbers - linear screening,


Code Template

public class Main {
    static final int N = 1000010;
    static int[] primes = new int[N]; //Store all prime numbers
    static int cnt; // Number of prime numbers
    static boolean[] st = new boolean[N]; // Is it screened
    
    static void get_primes(int n){ // O(n)
        for (int i = 2; i <= n; i ++ ) {
            if (!st[i]) primes[cnt ++ ] = i;
            for (int j = 0; primes[j] * i <= n; j ++ ) {
                st[primes[j] * i] = true; // Is to multiply the prime numbers before I by i, and get the total number, and then filter out true (Principle: Arithmetic Fundamental Theorem: Any integer can be decomposed into prime factors)
                if (i % primes[j] == 0) break; // Exit the loop when i traverse
            }
        }
    }
    
    public static void main(String[] args) {
        get_primes(100000);
        for (int i = 0; i < 20; i ++ ) System.out.println(primes[i]);
    }
}

Code