With the foundation of the red and black trees in front, our task in this section is relatively easy.
Let's explain what Map and Set are with the help of network literature.
First of all, we need to know that the bottom layers of Map and Set are red and black trees.
It is a balanced binary search tree, that is, binary balanced search tree.
set is the Key model we mentioned earlier, and map is the < K, V > model.
Next, we will introduce while comparing.
Introduction to set and map
Let's start with set:
By referring to the statement about set in the document, we can find that:

T here is what we call Key, which is key_type or value_type, that is, compare the size. These things are compared.
Then Compare is the way of comparison. It is an imitation function, which tells set how I Compare. Here you can refer to the related description of the linked list, which will not be repeated here.
Then, following the interface model below, we can simply create a set and traverse it.

Here are some member functions, there is nothing to say.

Functions like these, we've been using them for a long time. By analogy with the previous containers, we will skip them here. For details, we can see the following usage examples.
Let's take another look at the find function:
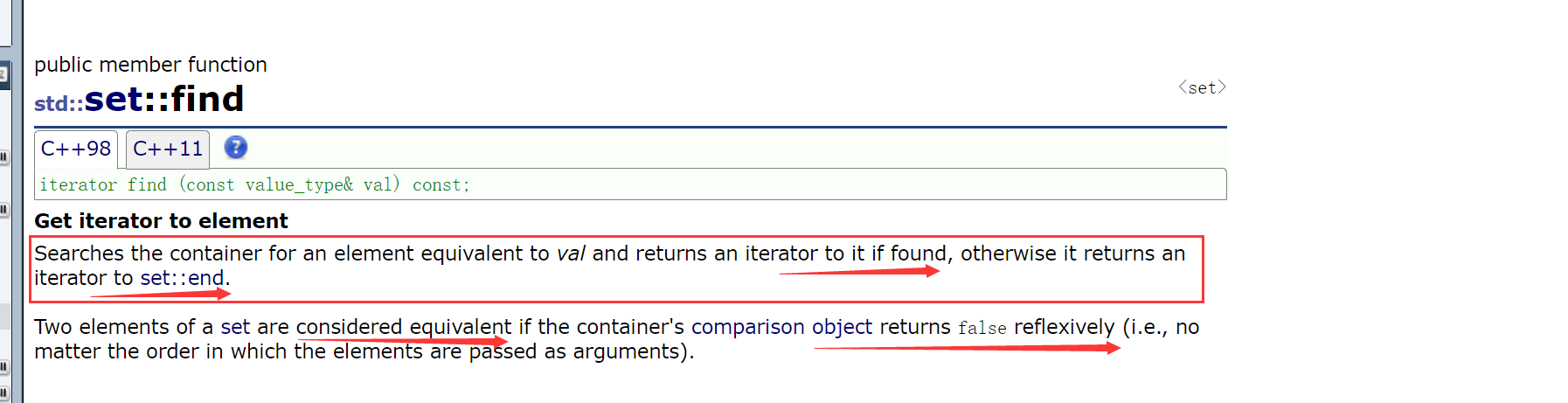
Its meaning is clear.
That is, when you find that location, you return the iterator of that location. Otherwise, set::end() is returned.
void test_set()
{
set<int> s; //establish
s.insert(3);
s.insert(4);
s.insert(8);
s.insert(10);
s.insert(1);
s.insert(26);
s.insert(7);
s.insert(2);
s.insert(3); //insert
set<int>::iterator is = s.begin(); //Define iterators
while (is != s.end())
{
cout << *is << " "; //Cyclic printing
is++;
}
cout << endl;
for (auto e : s) //Another printing method - print with range for
{
cout << e << " ";
}
//Sorting + de duplication
}
void test_set1()
{
set<string> ss;
ss.insert("hello"); //Insert string continuously
ss.insert("map");
ss.insert("set");
ss.insert("string");
ss.insert("wrong");
set<string>::iterator it = ss.find("wron"); //Find. If found, the iterator at the corresponding position will be returned. If not found
//Just return to SS end()
if (it == ss.end())
{
cout << "Can't find" << endl;
}
else
{
cout << "eureka" << endl;
}
}
int main()
{
test_set();
test_set1();
return 0;
}
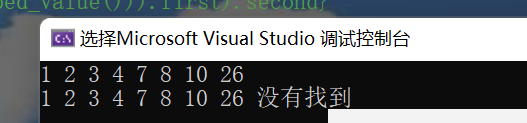
The printed results are shown in the figure above.
In the same way, let's take a look at map
In fact, map and set are very similar. It has one more parameter. (for the rotten K and V models mentioned above, when storing the Value of key, the Value of each key is followed by a Value)

As shown in the figure above, it is actually followed by a T. That is what we call value.
Its usage is slightly different from that of set, but we need to insert it with pair. As for what pair is, we mentioned it in the previous section. Here, let's say it again:

In other words, pair is essentially a class, which stores two types of values. Its use and advantage is that when a pair is returned, it is equivalent to returning two values.
So pair is equivalent to a packaged function. I pack the two values together and return them together. (but it is essentially a class)
Of course, we can also use make_pair come and go
make_pair is essentially a re encapsulation of pair type.
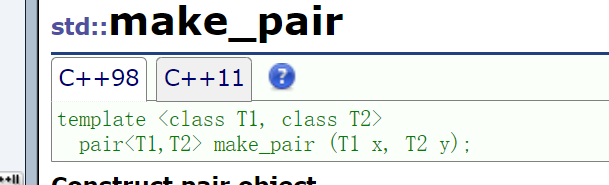
As you can see, a make_ The return value of pair is actually a pair.
The following code contains a lot of things, including different ways of writing a lot of content. You can taste it carefully.
void test_map1()
{
map<int, double> m; //K V model
m.insert(pair<int, double>(1, 1.1));//Call the constructor of pair to construct an anonymous object
m.insert(pair<int, double>(2, 2.1));
m.insert(pair<int, double>(5, 3.4));
m.insert(make_pair(2, 2.2)); //Call the function template and construct the object. The advantage is that there is no need to declare the parameters of pair,
//Let the function deduce by itself, which is more convenient to use
// If the key is the same, the insertion fails
map<int, double>::iterator it = m.begin();
while (it != m.end())
{
cout << (*it).first<<":"<<(*it).second << endl;
cout << it->first << ":" << it -> second << endl;
it++;
}
cout << endl;
}
void test_map2()
{
typedef map<string, string> DICT;
typedef pair<string, string> D_KV;
DICT dict;
dict.insert(D_KV("hello", "Hello"));
dict.insert(D_KV("fine", "I'm fine"));
dict.insert(D_KV("nice", "very good"));
dict.insert(D_KV("no", "Not good"));
dict.insert(D_KV("OK", "good"));
DICT::iterator it = dict.find("hello");
if (it != dict.end())
{
cout << it->second << endl;
string& str = it->second;
str.insert(0, "{");
str += "}";
cout << str << endl;
}
}
void test_map3()
{
//You can also read from the file!! File operation!!!
string arr[] = { "Apple","Apple" ,"Apple", "watermelon","Pear","watermelon","Durian","Banana","Banana","Apple" };
map<string, int> mp;
/*for (const auto& str : arr)
{
map<string, int>::iterator it = mp.find(str);
if (it != mp.end())
{
it->second++;
}
else
{
mp.insert(pair<string, int>(str, 1));
}
}*/
//Method of counting times 1
/*for (const auto& e : arr)
{
pair<map<string, int>::iterator, bool> ret = mp.insert(pair<string, int>(e, 1));
if (ret.second == false)
{
ret.first->second++;
}
}*/
//Statistical method 2
// The following is statistical method 3
for (const auto& e : arr)
{
mp[e]++; //The return value of [] is mapped_value, the first return value is an iterator of iterator, and the second is a value of bool type.
}
for (const auto& e : mp)
{
cout << e.first << ":" << e.second << endl;
}
map<string, string> dic;
dic.insert(make_pair("insert", "insert"));
dic["left"]; //insert
dic["left"] = "left"; //modify
dic["right"] = "right"; //Insert + modify
dic["left"] = "Left, remaining";
//mapped_value& operator[](const key_value& K)
//{ return (this->insert(make_pair(K,mapped_value())).first).second}
}
void test_map4()
{
string arr[] = { "Apple","Apple" ,"Apple", "watermelon","Pear","watermelon","Durian","Banana","Banana","Apple" };
map<string, int> mp;
for (const auto& e : arr)
{
mp[e]++; //The return value of [] is mapped_value, the first return value is an iterator of iterator, and the second is a value of bool type.
}
//Suppose you need to sort the fruit order
vector<map<string, int>::iterator> vp; //The purpose of using iterators is to reduce copy. Deep copy is a waste of time
map<string, int>::iterator it = mp.begin();
while (it != mp.end())
{
vp.push_back(it);
it++;
}
sort(vp.begin(), vp.end(), Comp());
//You can also directly use map sorting to copy the pair data
map<int, string,greater<int>> mmp;
for (const auto& e : mp)
{
mmp.insert(make_pair(e.second, e.first));
}
set<map<string, int>::iterator, Comp> SortSet; //You can also use set to row
while (it != mp.end())
{
SortSet.insert(it);
it++;
}
typedef map<string, int>::iterator M_IT;
priority_queue<M_IT, vector<M_IT>, Comp> pq;
while (it != mp.end())
{
pq.push(it);
it++;
}
}
void test_map5()
{
map<string, string> dict;
dict.insert(make_pair("left", "left"));
dict.insert(make_pair("left", "Or left"));
multimap<string, string> mdict;
mdict.insert(make_pair("left", "left")); //Allow key value redundancy; Does not exist []
mdict.insert(make_pair("left", "Or left"));
}One of the practical application values of map is to find a dictionary.
As shown in the above example, search through the value of the Key. If it is found, we can print its pair - > second.
That's all for the time being about the usage of map and set. It's still relatively simple
Let's look at its simulation implementation below:
Simulation Implementation of set and map:
We use a red black tree to encapsulate both map and set containers.
This time, we will focus on how to implement such encapsulation and the knowledge about the implementation of iterators. For some knowledge about red and black trees, this section is no longer the focus of attention.
Cut the crap. Let's go straight to the code. Still that sentence, everything is in the code. In fact, the simulation of iterators here is very similar to that of linked lists.
BRTree.h (we reuse the code of red black tree in the previous section)
#pragma once
#include<iostream>
using namespace std;
enum Colour
{
RED,
BLACK,
};
template<class T> //The template here is uniformly changed to T, that is, either K or pair < K, V >
struct RBTreeNode
{
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;
Colour _col; //Give a reference color (used to identify red or black)
RBTreeNode(const T& x) //Constructor of red black tree node
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_data(x)
,_col(RED)
{}
};
template<class T, class Ref, class Ptr> //T T& T*
struct __TreeIterator
{
typedef Ref reference;
typedef Ptr pointer;
typedef RBTreeNode<T> Node;
typedef __TreeIterator<T, Ref, Ptr> Self;
Node* _node;
__TreeIterator(Node* node)
:_node(node)
{}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &_node->_data;
}
bool operator != (const Self& s) const
{
return _node != s._node;
}
bool operator==(const Self& s) const
{
return !(_node != s._node);
}
Self operator++() //Front++
{
if (_node->_right)
{
Node* left = _node->_right;
while (left->_left)
{
left = left->_left;
}
_node = left;
}
else
{
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_right)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Self operator--()
{
if (_node->_left)//The left subtree of the root node is not empty
{
Node* right = _node->_left;//Then find the rightmost node of the left subtree
while (right->_right)
{
right = right->_right;
}
_node = right;
}
else
{
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_left)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
};
//iterator adaptor
template <class Iterator>
struct ReverseIterator
{
typedef typename Iterator::reference Ref;
typedef typename Iterator::pointer Ptr;
typedef ReverseIterator<Iterator> Self;
//Iterator extraction?
ReverseIterator(Iterator it)
:_it(it)
{}
Ref operator*()
{
return *_it;
}
Ptr operator->()
{
return _it.operator->();//?
}
Self& operator--()
{
++_it;
return *this;
}
Self& operator++()
{
--_it;
return *this;
}
bool operator !=(const Self& s) const
{
return !(_it == s._it);
}
Iterator _it;
};
template<class K, class T ,class KeyOfT>
class RBTree
{
typedef RBTreeNode<T> Node;
public:
typedef __TreeIterator<T, T&, T*> iterator;
typedef __TreeIterator<T, const T&, const T*> const_iterator;
typedef ReverseIterator<iterator> reverse_iterator;
reverse_iterator rbegin()
{
Node* right = _root;
while (right && right->_right)
{
right = right->_right;
}
return reverse_iterator(iterator(right));
}
reverse_iterator rend()
{
return reverse_iterator(iterator(nullptr));
}
iterator begin()
{
Node* left = _root;
while (left && left->_left)
{
left = left->_left;
}
return iterator(left);
}
iterator end()
{
return iterator(nullptr);
}
RBTree()
:_root(nullptr) //Constructor Initializers
{}
//Copy construction and operator implementation
void Destroy(Node* root)//Destroy function
{
if (root == nullptr)
return;
Destroy(root->_left); //Through continuous recursion, it is similar to binary search tree
Destroy(root->_right);
delete root;
}
~RBTree() //Destructor -- to call the destroy function
{
Destroy(_root);
}
Node* Find(const K& key) //Find (analogical search binary tree)
{
KeyOfT oft;
Node* cur = _root;
while (cur)
{
if (oft(cur->_data) > key)
{
cur = cur->_left;
}
else if (oft(cur->_data) < key)
{
cur = cur->_right;
}
else
{
return cur;
}
}
return nullptr;
}
pair<iterator ,bool> insert(const T& data)//insert
{
KeyOfT oft;
if (_root == nullptr)
{
_root = new Node(data);
_root->_col = BLACK;
return make_pair(_root, true);
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (oft(cur->_data) < oft(data))//If you want to implement musimap and musiset, it is (oft (cur - > _data) < = oft (data))
{
parent = cur;
cur = cur->_right;
}
else if(oft(cur->_data) > oft(data))
{
parent = cur;
cur = cur->_left;
}
else
{
return make_pair(iterator(_root), false);
}
}
Node* newnode = new Node(data);
newnode->_col = RED; //Marked red
if (oft(parent->_data) < oft(data))
{
parent->_right = newnode;
newnode->_parent = parent;
}
else
{
parent->_left = newnode;
newnode->_parent = parent;
}
cur = newnode; //The previous one is exactly the same as the insertion of search binary tree, so it is marked with color. I won't go into too much detail here
while (parent && parent->_col == RED) //If the father exists and the color is red, deal with it
{
//The key is to see uncle
Node* grandfather = parent->_parent;//And grandpa must exist
if (parent == grandfather -> _left) //If the father is the grandfather's left child
{
Node* uncle = grandfather->_right; //So my uncle is my grandfather's right child
if (uncle && uncle->_col == RED) //If Uncle exists and is red (case 1)
{
parent->_col = uncle->_col = BLACK;//Turn father and uncle black
grandfather->_col = RED; //Grandpa turned red
//Continue to process upward
cur = grandfather; //Give grandpa's position to grandson
parent = cur->_parent; //Father becomes grandfather's father
}
else //Case 2 + 3: uncle does not exist or uncle exists and is black
{
//Case 2: single rotation
if (cur == parent->_left) //If the child is the father's left child
{
RotateR(grandfather); //Right single rotation
grandfather->_col = RED; //Re discoloration
parent->_col = BLACK;
}
else//Case 3: double rotation
{
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK; //The final change is the color of grandfather and father
grandfather->_col = RED; //Grandfather's color turns red and father's color turns black
}
break;
}
}
else //parent == grandparent -> _ Right the situation is the same
{
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED)//Case 1
{
uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
else//Case 2 + 3
{
if (cur == parent->_right)
{
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else //cur is the father's left
{
//Double rotation
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
//End of insertion
break;
}
}
}
_root->_col = BLACK;
return make_pair(iterator(newnode), true);
}
//The rest will not be explained. It is the same as searching binary tree and AVLTree
//But the rotation here does not need to adjust the balance factor.
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
RotateL(parent->_left);
RotateR(parent);
}
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
RotateR(parent->_right);
RotateL(parent);
}
void RotateL(Node* parent) //Sinistral
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* parentparent = parent->_parent;
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
} //In pairs
subR->_left = parent;
parent->_parent = subR;//In pairs
//Connect the subject and find the organization
if (parent == _root)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (parentparent->_left == parent)
{
parentparent->_left = subR;
}
else
{
parentparent->_right = subR;
}
subR->_parent = parentparent;
}
}
void RotateR(Node* parent) //Right single rotation
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
subL->_right = parent;
Node* parentparent = parent->_parent;
parent->_parent = subL;
if (parent == _root)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
if (parentparent->_left == parent)
{
parentparent->_left = subL;
}
else
{
parentparent->_right = subL;
}
subL->_parent = parentparent;
}
}
bool _CheckBlance(Node* root, int blackNum, int count)
{
if (root == nullptr)
{
if (count != blackNum)
{
cout << "The number of black nodes varies" << endl;
}
return true;
}
if (root->_col == RED && root->_parent->_col == RED)
{
cout << "There are continuous red nodes" << endl;
return false;
}
if (root->_col == BLACK)
{
count++;
}
return _CheckBlance(root->_left,blackNum ,count)
&& _CheckBlance(root->_right, blackNum, count);
}
bool CheckBlance()
{
if (_root == nullptr)
{
return true;
}
if (_root->_col == RED)
{
cout << "The root node is red"<<endl;
return false;
}
//Find the leftmost path as the reference value of the black node
int blackNum = 0;
Node* left = _root;
while (left)
{
if (left->_col == BLACK)
{
blackNum++;
}
left = left->_left;
}
int count = 0;
return _CheckBlance(_root, blackNum, count);
}
private:
Node* _root;
};map.h
#pragma once
#include"BRTree.h"
namespace jxwd
{
template<class K, class V>
class map
{
public:
struct MapKeyOfT
{
const K& operator()(const pair<const K, V>& kv)
{
return kv.first;
}
};
typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;
typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::reverse_iterator reverse_iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
reverse_iterator rbegin()
{
return _t.rbegin();
}
reverse_iterator rend()
{
return _t.rend();
}
pair<iterator, bool> insert(const pair<const K, V>& kv)
{
return _t.insert(kv);
}
pair<iterator, bool> insert(const pair<K, V>& kv)
{
return _t.insert(kv);
}
V& operator[](const K& key)
{
pair<iterator, bool> ret = insert(make_pair(key, V()));
return ret.first->second;
}
private:
RBTree<K, pair<const K, V>, MapKeyOfT> _t;
};
}
set.h
#pragma once
#include "BRTree.h"
namespace jxwd
{
template<class K>
class set
{
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
typedef typename RBTree<K, K, SetKeyOfT>::iterator iterator;
typedef typename RBTree<K, K, SetKeyOfT>::reverse_iterator reverse_iterator;
reverse_iterator rbegin()
{
return _t.rbegin();
}
reverse_iterator rend()
{
return _t.rend();
}
bool insert(const K& k)
{
_t.insert(k);
return true;
}
iterator end()
{
return _t.end();
}
iterator begin()
{
return _t.begin();
}
private:
RBTree<K, K ,SetKeyOfT> _t;
};
}test.cpp
#include"set.h"
#include"map.h"
int main()
{
jxwd::map<int, int> t;
t.insert(make_pair(3, 3));
t.insert(make_pair(2, 2));
t.insert(make_pair(1, 1));
t.insert(make_pair(0, 7));
t.insert(make_pair(6, 2));
t[2] = 7;
jxwd::map<int, int>::reverse_iterator it = t.rbegin();
while (it != t.rend())
{
cout << (*it).first << ":" << (*it).second << endl;
cout << it->first<< ":" << it->second << endl;
++it;
}
jxwd::set<int> tt;
tt.insert(3);
tt.insert(1);
tt.insert(2);
tt.insert(4);
jxwd::set<int>::reverse_iterator sit = tt.rbegin();
while (sit != tt.rend())
{
cout << *sit << endl;
++sit;
}
cout << endl;;
return 0;
}
Screenshot of the last code run:
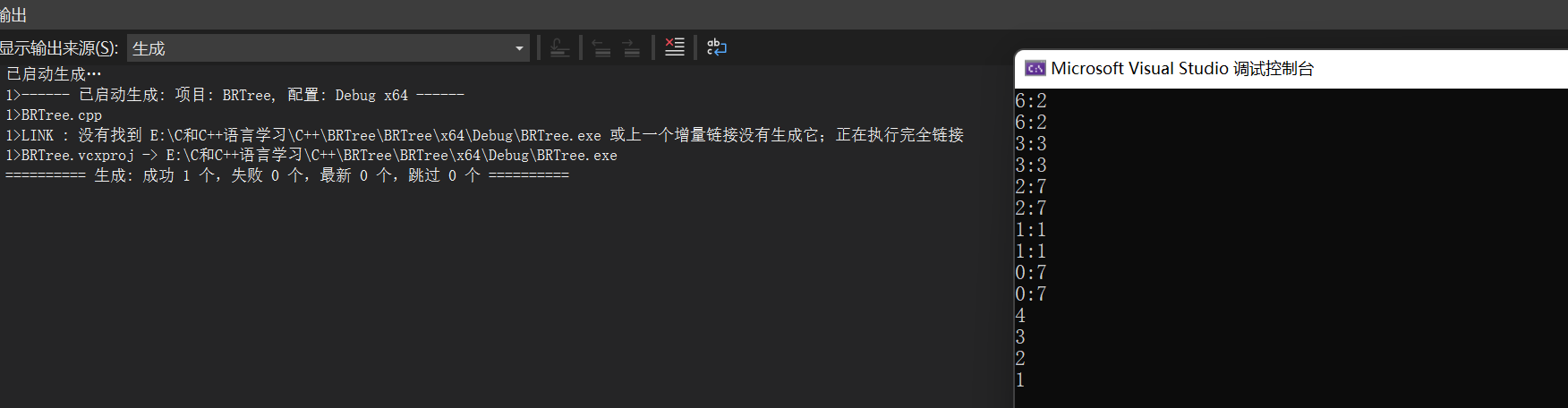
I'm really too lazy to type 😀, Everything is in the code.
I believe everyone can understand 😀.