In the previous article, we introduced bubble sorting and fast sorting in swap sorting, so this article will introduce selection sorting and heap sorting, and their comparison with fast sorting.

I. Direct Selection Sorting

1. Thought

Before describing the idea of direct selection ordering, let's start with a hypothesis. (Whatever the idea of ordering this hypothesis is.)

Suppose I have two sets, one is the set to be sorted, and the other is the empty set. Now I use this empty set to complete the sorting of the set to be sorted.

Step 1: I can traverse the listA collection, find the largest number of nums, and insert this num into listB.

listB.Insert(num);

listA.Remove(num);

Step 2: Repeat the first step until the number of listA sets is consumed.

In this way, the data will gradually flow from listA to listB. Finally, listB is an ordered set.

The code is as follows:

static List<int> InsertSort(List<int> listA)
{
    if (listA == null)
        return null;
    List<int> listB = new List<int>();
    int maxNum = 0;
    int ptr = 0;
    int i = 0;
    while (listA.Count > 0)
    {
        for (i = 0, ptr = 0, maxNum = listA[0]; i < listA.Count; i++)
        {
            if (listA[i] < maxNum)
            {
                maxNum = listA[i];
                ptr = i;
            }
        }
        listB.Add(maxNum);
        listA.RemoveAt(ptr);
    }
　　 listA = listB;
    return listA;
}

The idea of direct selection sort is the same as the idea here, except that it does not need to use intermediate set to sort, and it can be exchanged directly in its own set.

Next, to simplify the above process, you can select the sorted version directly:

static List<int> SelectionSort(List<int> list)
{
    int count = list.Count;
    //Number of times to traverse
    for (int i = 0; i < count - 1; i++)
    {
        //hypothesis tempIndex Minimum Subscript Value
        int tempIndex = i;

        for (int j = i + 1; j < count; j++)
        {
            //If tempIndex Subscript value greater than j Subscript value,Record smaller value Subscripts j
            if (list[tempIndex] > list[j])
                tempIndex = j;
        }

        //Finally, the hypothetical minimum is exchanged with the real minimum.
        var tempData = list[tempIndex];
        list[tempIndex] = list[i];
        list[i] = tempData;
    }
    return list;
}

 

 

2. Complexity

The time complexity of selection sort is O(n2). At first glance, how is it the same as that of bubble sort?

From the above code, the number of cycles to select the sort is as follows:

(n-1) + (n-2) + (n-3) + ... + 2 + 1

The results were: n2/2

Therefore, the time complexity of selecting sort is O(n2)

However, because there are few switching operations required for selection sort, at most n-1 switching occurs.

Bubble sorting is a two-to-two swap. At most, n2/2 swaps occur. Therefore, the performance of the selection of sorting is still due to bubble sorting.

This is also the last article, I will ask, why exchange every time, and can not find the maximum / minimum value, before the exchange operation.

 

II. Heap Sorting

1. Thought

1. Prelude

I believe many people like to watch basketball games, especially the nba playoffs, so first look at how the playoffs are promoted.

 

The nba playoffs are a step-by-step way to determine the final winner. Can I use this form for ranking?

1. Look at the three squares in the lower left corner. Two are level 4 and one is level 3. Assuming that there is a number in each square, which is different in size, can I compare the three numbers and then put the largest one in level 3?

2. If every three squares can be compared in this way, will a maximum value be determined and put into the only one at level 1?

There's another problem here. What if there are only two squares? One is on top, the other is on the bottom, not two on the bottom, because there needs to be a promotion.

 

2) Binary Reactor

Does the picture above look familiar and feel like a binary tree structure? Here is the binary heap.

Since we want to map a set of data into a binary heap, we need to understand how this set of data is stored and mapped.

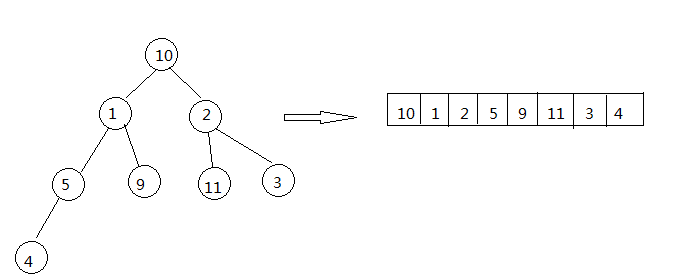
Mapping from top to bottom, from left to right. From the graph, the corresponding subscript range of each level is: 2n-1-2 (2n-1).

The next step is to sort him in a heap: just judge the parent node.

Here's the order of comparison: the parent node's order of comparison is from bottom to top, from right to left. And the node exchanged with the parent node also needs to be compared with the descendant node to determine its location.

Demo:

 

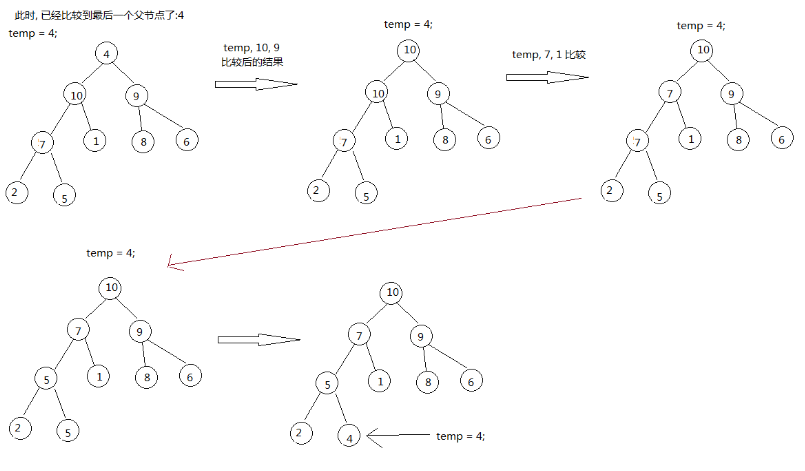
Comparing a parent node, the code is as follows:

static void HeapAdjust(List<int> list, int parent, int length)
{
    //temp Save the current parent node
    int temp = list[parent];

    //Get the left child's subscription(This is the definition of binary tree, you can see from the picture.)
    int child = 2 * parent + 1;

    while (child < length)
    {
        //If parent If you have a right child, you should judge whether the left child is smaller than the right child.
        if (child + 1 < length && list[child] < list[child + 1])
            child++; //At this point child Point to the right child

        //The parent node is larger than the child node, so there is no need for swapping.
        if (temp >= list[child])
            //It can be written here., that is because temp All nodes under nodes, They've all been filmed in sequence., It ensures that the parent node is the largest of the child nodes.
            break; 

        //Assigning the value of the larger child node to the parent node
        //This is equivalent to forward coverage., because temp It has been taken out., So it's equivalent to having a pit to fill in.
        list[parent] = list[child];

        //Here's how to prepare for the next cycle
        //In other words, Give Way parent point temp One of the large subnodes
        //The child node is then used as the next parent node
        parent = child;

        //Find the left child node of the new parent node
        child = 2 * parent + 1;
    }
    //Finally, temp Values are assigned to larger subnodes to form a two-value exchange
    list[parent] = temp;
}

Next comes the code for heap sorting.

///<summary>
/// Heap sorting
///</summary>
///<param name="list"></param>
public static void HeapSort(List<int> list)
{
    //list.Count/2-1 Is the subscript of the last parent node, All parent nodes are forward
    for (int i = list.Count / 2 - 1; i >= 0; i--)
    {
        HeapAdjust(list, i, list.Count);
    }

    //The final output heap element
    for (int i = list.Count - 1; i > 0; i--)
    {
        //Value alignment between the top of the heap and the last element of the current heap
        int temp = list[0];
        list[0] = list[i];
        list[i] = temp;

        //Remoulding Heap, Because the last element of the heap will be removed
        //Excluded data, Ordered data
        HeapAdjust(list, 0, i);
    }
}

The idea here is to constantly build the heap, get the maximum value, list[0], and then exchange the maximum value with the last value of the heap, eliminate the maximum value, and re-shape the heap. At this time, the heap has lost a value.

That is to say, there are 10 heap sorting numbers at the beginning, after a round, the maximum value is eliminated, and then the heap sorting time, there are only 9 values.

 

2. Complexity

The time complexity of heap sorting is O(nlog2n). In terms of complexity, it seems to be the same as fast sorting, so is it true?

The certification process is shown in the following reference link

 

3. Heap Sorting vs Quick Sorting

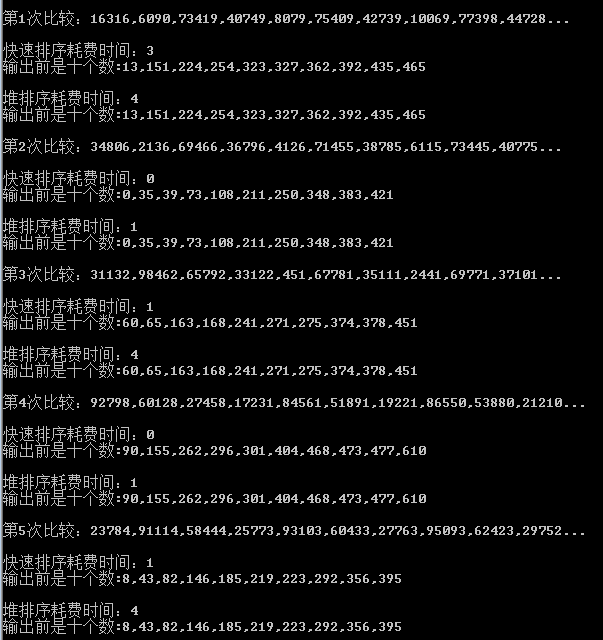
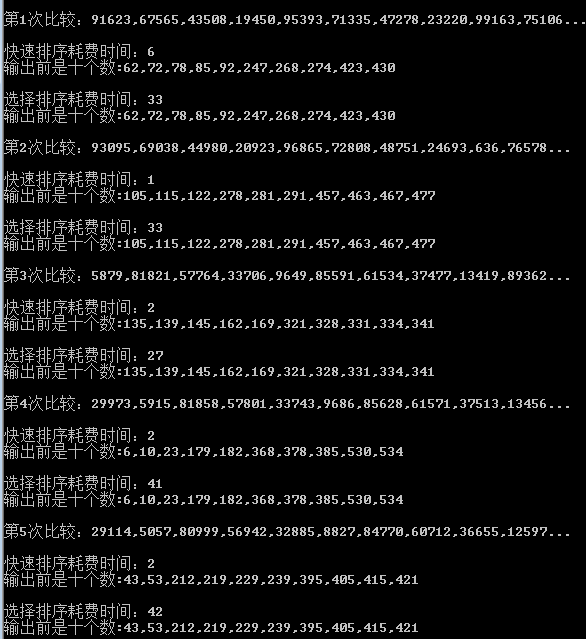
From the above point of view, in 2000 data volume, heap sorting is slow and fast, no wonder Microsoft will use fast sorting.

So is heap sorting useless?

Quick sorting can't extract some of the largest/smallest numbers without completing the sorting, but selective sorting and heap sorting are good at this, and can extract some of the largest/smallest data without completing the reordering.

Reference resources:

Algorithms Series 15 Days Quick - Seven Classic Sorting the Next Day

Heap Sorting of Sorting Algorithms and Its Time Complexity and Space Complexity