1, The idea of selecting sorting method: first take out the smallest (large) element, then take out the smallest (large) element in the remaining elements, and select the smallest (large) element among the unprocessed elements for sorting each time.

1. Two ideas:

① open up a new array space and put the smallest (large) elements in the new array for sorting

② sort in place and exchange elements in the source array.

2, Implementation of algorithm

1. Implementation of spatial sorting algorithm:

    /**
     * Open up space and sort in different places
     * Sort the elements of an array (output from small to large), and select sort
     */
    public static void sortArray2(int[] array){
        /*
        newArray//As an element to store the newly sorted array.
         */
        int[] newArray=new int[array.length];//Define a new array (new space)
        for (int i=0;i<array.length;i++){
            int minIndex=i;
            for (int j=i;j<array.length;j++){
                if (array[j]<array[minIndex]){
                    minIndex=j;
                }
                newArray[i]=array[minIndex];
            }
            array[minIndex]=array[i];//The smallest element cannot be cycled repeatedly and should be overwritten.
        }
        System.out.println(Arrays.toString(newArray));
    }

Such a sorting idea is simple, but it causes a waste of space, so we need to optimize the selection and sorting.

2. The idea of in-situ sorting is as follows:

            

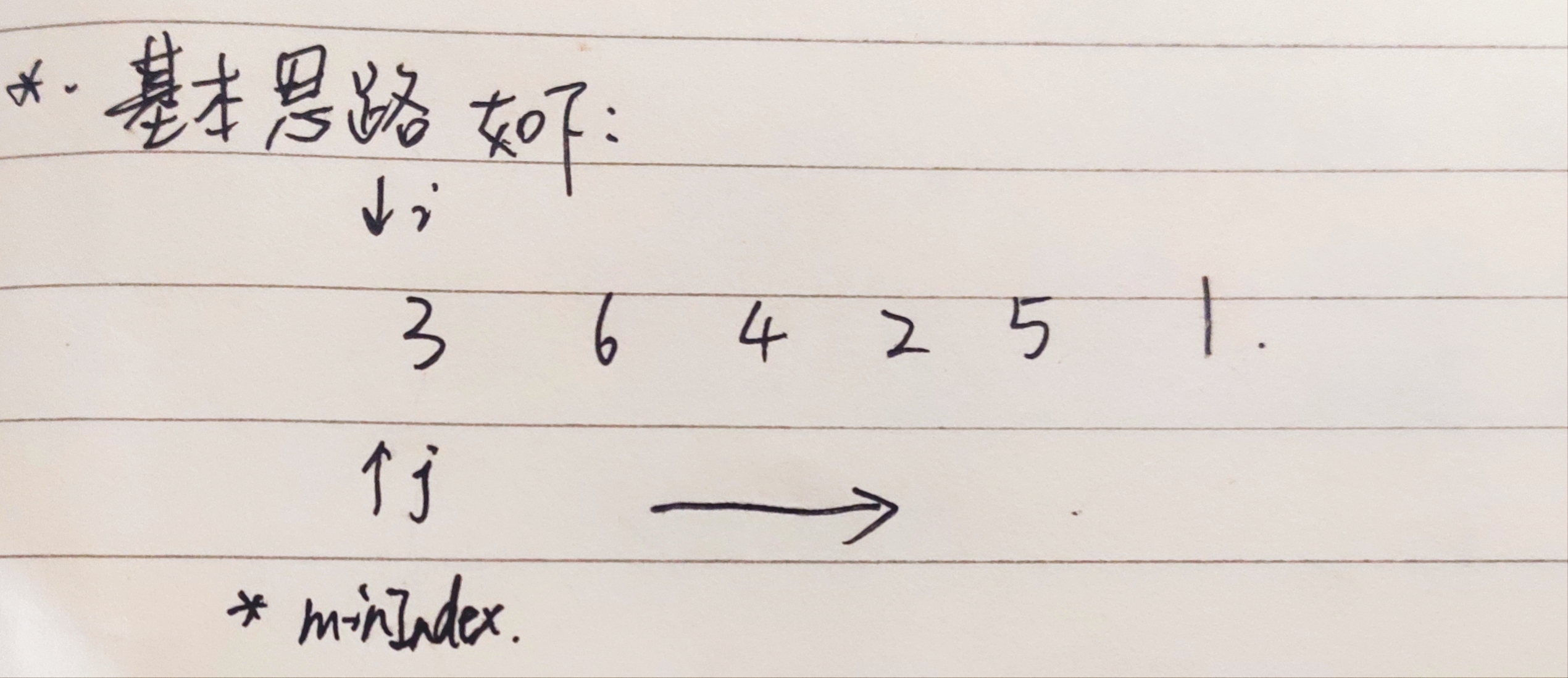
Parsing: set the i index as the beginning of the cycle and i as the outer cycle. After the cycle starts, set the minimum index as minIndex and tentatively as the element of index i, and then retrieve it from J. at this time, j=i. if the element at the j index position is less than the element at the minIndex index position, replace the minimum index minIndex with the current j; After the inner loop passes through, you can get the minimum value of the whole array (because this is the first loop). Each loop can find the minimum value within the range of [i, array.length). Then, you can exchange the obtained minimum value with the i element of the current outer loop, so as to complete in-situ sorting.

Note: the common pattern of element exchange: define a swap as an intermediate variable for exchange.

3. Algorithm implementation:

 /**
     * in-place sort 
     * Sort the elements of an array (output from small to large), and select sort
     */
    public static void sortArray1(int[] array) {
        /*int i = array[0];//Take out the first element and compare it with other elements in the array one by one. If it is greater than, replace it, otherwise it remains unchanged.
        int j;//Record the index of array elements to be compared and scanned, and scan arr[j,arr.length-1].
        int minIndex = 0;//Record the index of the replaced element after comparison
        int swap=0;As an intermediate variable in exchange (fixed mode)*/
        for (int i = 0; i < array.length; i++) {
            int minIndex=i;
            for (int j=i;j<array.length;j++){
                if (array[j]<array[minIndex]){
                    minIndex=j;
                }
            }
            //Exchange
            int swap=array[i];
            array[i]=array[minIndex];
            array[minIndex]=swap;
        }
       for (int k=0;k<array.length;k++){
           System.out.println(array[k]);
       }
    }

4. As a method, it should conform to the reusability of the method. Therefore, the method should be generalized as follows:

/**
     * Optimize selection sorting and in-situ sorting to improve the reusability of the algorithm -- that is, generalization.
     * Generic method: add < E > after the modifier. The function of extends comparable is to limit the parameters to be comparable (only receive the types of inherited classes and their subclasses).
     *         ** If it is super, the parameter only receives this class and its parent class.
     */
    public static <E extends Comparable<E>> void selectSort(E[] array){
        for (int i=0;i<array.length;i++){
            int minIndex=i;
            for (int j=i;j<array.length;j++){
                if (array[j].compareTo(array[minIndex])<0){//The comparableTo method is equivalent to the subtraction order. If the result is greater than zero, the former is greater than the latter;
                                                           //Otherwise, it is less than, and if they are equal, they are equal to zero.
                    minIndex=j;
                }
                //Exchange element positions to realize sorting
                E swap=array[i];
                array[i]=array[minIndex];
                array[minIndex]=swap;
            }
        }
        System.out.println(Arrays.toString(array));
    }

For the above methods, when testing, the array should be a comparable data type, not a basic data type, but its wrapper class. Expected generic, cannot be a base data type.

3, Analysis of algorithm complexity

From the implementation of the above algorithm, we can see that the retrieved elements are gradually reduced during the process of the program, which is similar to

 1+2+3+4+...+n, so we can list the formula of its complexity: 1/2n^2+1/2n. In addition, in the algorithm complexity analysis, the complexity of constant level can be ignored, that is, one-half of the coefficient before n square, and then n is lower than n square. When the data reaches a certain scale, it is also ignored, so the complexity of the algorithm is O(n^2).