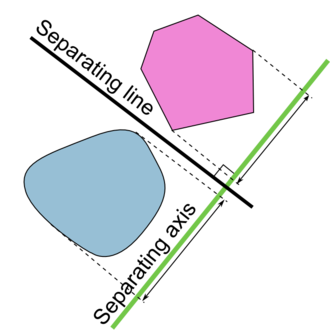
Collision detection can be divided into   Broad Phase   (Rough inspection) and   Narrow Phase   (fine detection) two stages. In the rough detection stage, we can directly compare whether the AABB bounding boxes of two objects collide, so as to save computation and time. In fine detection, SAT (separating axis theory) collision detection algorithm is intuitive and efficient, and its principle is clear and easy to understand, that is, if two objects do not collide, there will always be a straight line that can separate the two objects. The separation axis is applicable to the detection between convex polygons, not concave polygons. For the detection of concave polygons, the concave polygons can be divided into multiple convex polygons by algorithm and then calculated.

The algorithm steps are as follows:

Step 1: take out an edge from the polygon to be detected and find its normal vector, which will be our "projection axis".

Step 2: loop through each point of the first polygon and project them onto this axis.

Step 3: do the same for the second polygon.

Step 4: get the projections of the two polygons respectively, and detect whether the two projections overlap.

If you find a gap between the two "shadows" projected on the axis, the two figures must not intersect. But if there is no gap, they may touch. You need to continue to detect until each edge of the two polygons is detected. If you don't find any gaps after detecting each edge, they collide with each other.

According to the above steps, the key codes for collision detection between two convex polygons are as follows (refer to collision.py):

 1 def flatten_points_on(points, normal, result):
 2     minpoint = math.inf
 3     maxpoint = -math.inf
 4 
 5     for i in range(len(points)):
 6         dot = points[i].dot(normal)
 7         if dot < minpoint:
 8             minpoint = dot
 9         if dot > maxpoint:
10             maxpoint = dot
11 
12     result[0] = minpoint
13     result[1] = maxpoint
14 
15 
16 def is_separating_axis(a_pos, b_pos, a_points, b_points, axis):
17     range_a = [0, 0]
18     range_b = [0, 0]
19 
20     offset_v = b_pos-a_pos
21 
22     projected_offset = offset_v.dot(axis)
23 
24     flatten_points_on(a_points, axis, range_a)
25     flatten_points_on(b_points, axis, range_b)
26 
27     range_b[0] += projected_offset
28     range_b[1] += projected_offset
29 
30     if range_a[0] > range_b[1] or range_b[0] > range_a[1]:
31         return True
32 
33     return False
34 
35 
36 def test_aabb(b1,b2):
37     return b1[0][0] <= b2[1][0] and b2[0][0] <= b1[1][0] and b1[0][1] <= b2[2][1] and b2[0][1] <= b1[2][1]
38 
39 
40 def test_poly_poly(a, b):
41     a_points = a.rel_points
42     b_points = b.rel_points
43     a_pos = a.pos
44     b_pos = b.pos
45 
46     for n in a.normals:
47         if is_separating_axis(a_pos, b_pos, a_points, b_points, n):
48             return False
49 
50     for n in b.normals:
51         if is_separating_axis(a_pos, b_pos, a_points, b_points, n):
52             return False
53 
54     return True
55 
56 
57 def collide(a, b):
58     if not test_aabb(a.aabb, b.aabb):
59         return False
60 
61     return test_poly_poly(a, b)

  For the two convex polygons specified by the parameter, the collision detection function collide first calls test_aabb to determine whether their AABB bounding boxes intersect. If the outer bounding boxes do not intersect, it proves that there is no collision between the two polygons, and the function value returns False. On the contrary, the separation axis algorithm is used for fine detection. The function test_poly_poly follows the algorithm flow For each edge, if there is a separation axis on one edge so that the projections of two polygons on it do not coincide, it proves that the polygons do not intersect and returns False directly. The function is_separating_axis calculates whether the projections of polygons on the separation axis vector coincide according to the given positions of two polygons, the local coordinates of polygon vertices and the separation axis vector.

It should be noted that for many graphic views and animation frames, the graphic item is generally drawn using its own local coordinate system, usually with its center as the origin, and the position of the graphic item is the position of its origin in its parent graphic item or scene. The Coordinate Datum in the separation axis judgment function should be consistent, if the position of the first input parameter polygon $a $is used as the reference At the origin, the local coordinates of the vertex coordinates of polygon $b $under this reference system should be added with the offset of $\ overrightarrow {AB} $, so the offset after the projection of polygon $b $to the separation axis should also be added with the offset after the projection of $\ overrightarrow {AB} $$  \ overrightarrow{ab} \cdot \overrightarrow{n}$

reference resources:

collision.py

Hyperplane separation theorem

SAT (Separating Axis Theorem)

Explanation of separation axis theorem algorithm for collision detection

2D convex polygon collision detection algorithm (I) - SAT