1. Sequential storage representation of linear tables

• Sequential storage: A storage structure that is logically and physically adjacent. A set of memory cells with consecutive addresses stores data elements in a linear table in turn. This can be done with a static array V[n] or a dynamic array.
• Address calculation formula: LOC(ai) = LOC(a0) base address + i × C The same data type takes up the same size of space.
• The characteristics of the sequence table:

        (1) High storage density: storage density = the storage space required for the value of a data element / the storage space actually required for that element. However, you need to pre-allocate "enough" space, which can result in a waste of storage space.

        (2) Easy random access.

        (3) It is not easy to insert and delete because it will cause a large number of nodes to move.

2. Description of Sequential Table Classes

• Array space should be defined as "large enough" to be maxSize as needed. Considering that the length of a linear table is variable, a variable curLen is needed to record the current actual length of the linear table.
• Java code implementation:

package LinearList;

public class SqList implements IList{
	
	private Object[] listElem;
	private int curLen;
	
	public SqList(int maxSize) {
		curLen = 0;
		listElem = new Object[maxSize];
	}
}

3. Implementation of Basic Operations on Sequence Table

• Java code implementation:

package LinearList;

public class SqList implements IList{
	
	private Object[] listElem;
	private int curLen;
	
	public SqList(int maxSize) {
		curLen = 0;
		listElem = new Object[maxSize];
	}
	
	public void clear() {
		curLen = 0;
	}
	
	public boolean isEmpty() {
		return curLen == 0;
	}
	
	public int getLength() {
		return curLen;
	}
	
	public Object getValue(int i) throws Exception{
		if(i<0 || i>curLen-1)
			throw new Exception("No."+i+"Elements do not exist");
		return listElem[i];		
	}
	
	public void display() {
		for(int j=0;j<curLen;j++) 
			System.out.println(listElem[j]);
	}
	
	public void expandSpace(int newMaxSize) {
		Object[] newArr = new Object[newMaxSize];
		for(int i=0;i<listElem.length;i++)
			newArr[i]=listElem[i];
		listElem = newArr;
	}
	
	public void insert(int i,Object x) throws Exception{
		if(curLen == listElem.length)
			throw new Exception("Sequence table full");
		if(i<0 || i>curLen)
			throw new Exception("Illegal insertion position");
		for(int j=0;j>i;j--)
			listElem[j]=listElem[j-1];
		listElem[i]=x;
		curLen++;
	}
	
	public void remove(int i)throws Exception{
		if(i<0 || i>curLen-1)
			throw new Exception("Illegal Delete Location");
		for(int j=i;j<curLen-1;j++)
			listElem[j]=listElem[j+1];
		curLen--;
	}
	
	public int indexOf(Object x) {
		int j=0;
		while(j<curLen && !listElem[j].equals(x))
			j++;
		if(j<curLen)
			return j;
		else
			return -1;
	}

}

4. Introduction of several important methods and performance analysis of algorithms

1. Insert operation: Insert an element with a value of x before the first element ai, where 0 < I < curLen. When i=0, insert in the header; When i=curLen, insert at the end of the table.

Algorithmic steps:

(1) Detect if the space is full, throw an exception or call the expansion method if it is full.

(2) To judge the validity of parameter i, it is valid when 0 < I < curLen.

(3) Move the insertion position and all subsequent elements back one position. Note: You must move one by one from the last data element.

(4) Insert elements with a table length of 1.

Performance analysis: Inserting before the first data element causes n-i data elements to move backwards. Assuming that the probability of inserting before the first element is Pi, the average number of times an element is moved with equal probability:

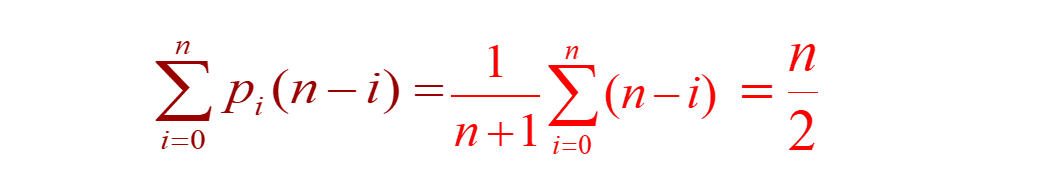
So the time complexity is O(n).

2. Delete operation: delete the data element at the first position from the order table.

Algorithmic steps:

(1) Judge the validity of parameter i, throw an exception if I < 0 || I > curLen-1 is not valid.

(2) Move all elements after the first element forward by one position.

(3) Table length minus 1.

Performance analysis: Deleting the first data element causes n-1-i data elements to move forward. Assuming the probability of deleting the first element is pi, the average number of times an element is moved with equal probability:

                        

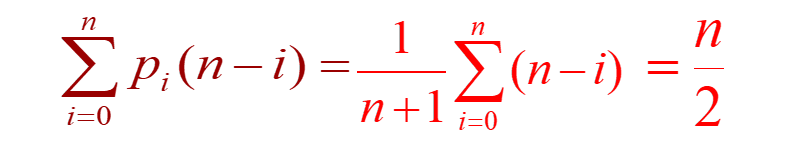
So the time complexity is O(n).

3. Find by value operation: Find if data element x exists in the order table, if it exists, return the location where x first appeared, otherwise return -1.   

          Algorithmic step: Compare each element from beginning to end, return its bit number if it is equal, otherwise return -1.

          Performance analysis: if the data element x to be found is the first i in the sequence table   i+1 comparisons are required for locations, so under equal probability conditions, the average number of comparisons of data elements is:

     

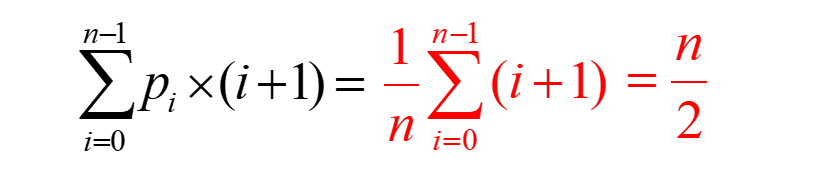
          So the time complexity is O(n).

5. Summary of this section

The implementation of arrays allows random access operations to take only a constant amount of time, and traversal of linear tables is performed in linear time. However, insertion and deletion are too expensive, moving half the elements on average, and therefore require linear time. On the other hand, if all operations occur at the high end of the table, there are no elements to move, and insertion and deletion only take O(1) time.

There are many real-world situations, such as a roster, where tables are usually built with high-end insertions followed by only access to arrays. In this case, the array order table is an appropriate implementation. However, inserting and deleting tables frequently (especially on the front end) is not a good option.