Sort, also known as Sort Algorithm, is the process of sorting a set of data according to a specified message.
Sorted classification:
1) Internal sorting: means that all data that needs to be processed is loaded into internal memory for sorting. Internal sorting includes insert sort (direct insert or Hill sort), select sort (simple sort and heap sort), exchange sort (bubble sort and quick sort), merge sort, cardinality sort.
2) External Sorting: The amount of data is too large to be loaded into memory, so external storage is needed to sort.
- Bubble sort #
- Select Sort #
- Insert Sort #
- Shell Sort #
- Quick Sort #
- Merge Sort #
- Cardinality sorting #
- Summary and comparison of common sorting algorithms #
1. Bubble sort
The principle of bubble sorting is to compare two adjacent elements to each other, swapping large (or small) numbers with the latter. In this way, the largest (or smallest) elements are ranked at the end of the queue, the next last, the next last... in each round of comparison. You can queue up.
The case of bubble sorting:
Bubble sorting rule:
1. Sort number is array length-1 (outer loop)
2. The number of comparisons needed for each sort decreases gradually, and the number of comparisons needed for the nth sort is array length-n-1 (inner loop)
Example: Array {1,3,4,2} Array length 4
Number of external cycles (4-1)
The number of inner loops is (4-current sort-1)
The following cases not only have the function of bubble sorting, but also can customize the reverse order sorting rule, which adds the optimization method of bubble sorting.
public class BubbleSort {
/**
* Bubble sorting rule
* Sort number is array length-1 (outer loop)
* The number of comparisons needed for each sort decreases gradually, and the number of comparisons for the nth sort is the array length-n-1 (inner loop)
* Example: Array {1,3,4,2} Array length 4
* Number of external cycles (4-1)
* The number of inner loops is (4-current sort-1)
*/
public static void bubbleSort(int[] arr,Sort sortType){
for (int i = 1; i < arr.length; i++) {
boolean flag = false; //Used to determine if a digital exchange has occurred
for (int j = 0; j < arr.length-i; j++) {
int a = arr[j];
int b = arr[j+1];
if(sortType==Sort.POSITIVE_SEQUENCE&&a > b){//Positive order places large values back
arr[j+1] = a;
arr[j] = b;
flag = true;
}else if(sortType==Sort.INVERTED_ORDER&&a < b){//Put small values back in reverse order
arr[j+1] = a;
arr[j] = b;
flag = true;
}
}
if(!flag){
System.out.printf("Sort completed, current sort is first%d Secondary sorting.\n",i);
break;
}
}
}
public static void main(String[] args) {
int[] arr = new int[8000];
for (int i = 0; i < 8000; i++) {
arr[i] = new Random().nextInt(8000);
}
long begin = System.currentTimeMillis();
bubbleSort(arr,Sort.POSITIVE_SEQUENCE);
long end = System.currentTimeMillis();
System.out.println((double)(end-begin)/1000 + "s");
}
}
enum Sort{
POSITIVE_SEQUENCE,
INVERTED_ORDER
}
2. Select Sort
Selective sorting is an internal sorting method in which the largest (smallest) in the search queue is first compared and the largest (smallest) after the first is placed in the second, so that the search is done in turn until the queue is sorted. Each lookup of the selection sort will only have one swap.
code implementation
public class SelectionSort {
/**
* Select Sort
* @param arr
* @param sortType
*/
public static void sort(int[] arr,Sort sortType){
for (int i = 0; i < arr.length-1; i++) {
int k = i;//The subscript for the maximum (small) value, initially defaulting to the current element
for (int j = i +1; j < arr.length; j++) {
if(sortType == Sort.POSITIVE_SEQUENCE && arr[k] > arr[j]){
k = j;//Save smaller tabs
}else if(sortType == Sort.INVERTED_ORDER && arr[k] < arr[j]){
k = j;
}
}
//Swap the resulting maximum (minimum) value with the current sorting position
int temp = arr[i];
arr[i] = arr[k];
arr[k] = temp;
}
}
public static void main(String[] args) {
int[] arr = new int[8000];
for (int i = 0; i < 8000; i++) {
arr[i] = new Random().nextInt(8000);
}
long begin = System.currentTimeMillis();
SelectionSort.sort(arr,Sort.INVERTED_ORDER);
long end = System.currentTimeMillis();
System.out.println((double)(end-begin)/1000+"Select sort efficiency in seconds");
for (int i : arr) {
System.out.print(i+"\t");
}
}
}
enum Sort{
POSITIVE_SEQUENCE,
INVERTED_ORDER
}
3. Insert Sort
The idea of inserting sort is to consider the data queue to be sorted as a combination of an ordered list and an unordered list, and to consider the first value arr[0] as an ordered value, to compare the value of arr[1] with that of arr[0], to sort a new ordered list based on the comparison results, and to compare the value of arr[2] with that of the previous ordered list. This completes the sorting of the data queue by comparing each subsequent value to the value in the sequential table.
public class InsertSort {
public static void main(String[] args) {
int[] arr = new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i] = (int) (Math.random() * 8000000);
}
long begin = System.currentTimeMillis();
insertSort(arr);
long end = System.currentTimeMillis();
System.out.println((double)(end-begin)/1000 + "s");
}
public static void insertSort(int[] arr) {
int insertVal = 0;
int insertIndex = 0;
for(int i = 1; i < arr.length; i++) {
insertVal = arr[i];//Value to compare
insertIndex = i - 1;//Previous element subscript
while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];// Move element backward
insertIndex--;
}
if(insertIndex + 1 != i) {
arr[insertIndex + 1] = insertVal;
}
}
}
}
Problem with insert sort: When the queue to be sorted is expected to have the top data at the end of the queue, there is too much backward (swap) operation at this time. Solution (optimized using Hill sorting)
4. Hill Sorting
Hill sorting is an optimization of simple insert sorting. The idea of Hill sorting is that the queues to be sorted are grouped by a certain increment, and each group is sorted by an insert sorting algorithm; As the increment decreases, each group contains more and more elements. When the increment decreases to 1, the entire queue is divided into exactly one group and the algorithm terminates.
/**
* Hill sorting: Insert sorting has one drawback: its worst case is when the queue expects the top data to be at the bottom of the queue.
* There are too many backward (swap) operations at this time. Hill sorting is an optimization of this problem.
*/
public class ShellSort {
public static void main(String[] args) {
int[] arr = {8,9,1,7,2,3,5,4,6,0};
shellSort2(arr);
for (int i : arr) {
System.out.print(i + " ");
}
System.out.println();
int[] arr1 = new int[80000];
for (int i = 0; i < 80000; i++) {
arr1[i] = (int) (Math.random() * 8000000);
}
long begin = System.currentTimeMillis();
shellSort(arr1);
long end = System.currentTimeMillis();
System.out.println((double)(end-begin)/1000 + "s");//Test duration 12s
int[] arr2 = new int[80000];
for (int i = 0; i < 80000; i++) {
arr2[i] = (int) (Math.random() * 8000000);
}
long begin2 = System.currentTimeMillis();
shellSort2(arr2);
long end2 = System.currentTimeMillis();
System.out.println((double)(end2-begin2)/1000 + "s");//Test duration 0.023s
}
//Exchange method
public static void shellSort(int[] arr){
int temp = 0;
for (int gap = arr.length/2; gap > 0;gap /= 2) {
//First round of Hill sort
//Because in the first round of sorting, 10 data are divided into five groups
for (int i = gap; i < arr.length; i++) {
//Traverse the elements in each group with a step of 5
for (int j = i-gap; j >= 0; j -= gap) {
if(arr[j] > arr[j+gap]){
temp = arr[j];
arr[j] = arr[j+gap];
arr[j+gap] = temp;
}
}
}
}
}
//displacement method
public static void shellSort2(int[] arr){
for (int gap = arr.length/2; gap > 0;gap /= 2) {
for (int i = gap; i < arr.length; i++) {
int j = i;
int temp = arr[j];
if(arr[j] < arr[j-gap]){
while (j - gap >= 0 && temp < arr[j-gap]){
arr[j] = arr[j-gap];
j -= gap;
}
arr[j] = temp;
}
}
}
}
}
5. Quick Sorting
Quick sorting idea: Separate the queue to be sorted into two queues by one sort, where the data in one queue is always less than the value in the other. Sort the two parts separately by the same algorithm (recursively) to make the whole queue an ordered list.
public class QuickSort {
public static void main(String[] args) {
// int[] arr = {-9,78,23,-567,70};
int[] arr = new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i] = new Random().nextInt(800000);
}
long begin = System.currentTimeMillis();
QuickSort.sort(arr,0,arr.length-1);
long end = System.currentTimeMillis();
System.out.println((double)(end-begin)/1000);//Test result is 0.03s
for (int i : arr) {
System.out.print(i + " ");
}
}
/**
* @param arr
* @param left
* @param right
*/
public static void sort(int[] arr,int left,int right){
int l = left;//Left Subscript
int r = right;//Right Subscript
//pivot median
int pivot = arr[(left + right)/2];
int temp = 0;
//The purpose of the while loop is to put a value smaller than pivot to the left
//Values larger than pivot are placed to the right
while (l < r){
//Look from left to right of pivot and exit only if you find a value less than or equal to pivot
while (arr[l] < pivot){
l += 1;
}
//Look left from right of pivot and exit only if you find a value greater than or equal to pivot
while (arr[r] > pivot){
r -= 1;
}
//Exit once l and r are both ordered
if(l >= r){
break;
}
temp = arr[l];
arr[l] = arr[r];
arr[r] = temp;
//If the swap finishes, find this arr[l] = pivot -- move forward
if(arr[l] == pivot){
r -= 1;
}
// 345 Scale 4
//If the swap is complete, the arr[r] = pivot ++ is found to move back
if(arr[r] == pivot){
l += 1;
}
}
if(l == r){
l += 1;
r -= 1;
}
//Recursion Left
if(left < r){
sort(arr,left,r);
}
//Recursion Right
if(right > l){
sort(arr,l,right);
}
}
}
6. Merge Sort Method
Quicksort is an improvement on bubble sorting. The basic idea is that the data to be sorted is divided into two separate parts by one-time sorting, in which all the data in one part is smaller than all the data in the other part. Then the two parts are sorted quickly by this method, and the whole sorting process can be done recursively so that the whole data becomes an ordered sequence.
public class MergeSort {
public static void main(String[] args) {
int[] arr = new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i] = (int) (Math.random() * 8000000);
}
int temp[] = new int[arr.length];
long begin = System.currentTimeMillis();
mergeSort(arr,0,arr.length-1,temp);
long end = System.currentTimeMillis();
System.out.println((double)(end-begin)/1000 + "s");//Test duration 0.014s
}
/**
*
* @param arr Sorted original array
* @param left Initial index of left ordered sequence
* @param mid Intermediate Index
* @param right Right Index
* @param temp Array to be transferred
*/
//Method of merging
public static void merge(int[] arr,int left,int mid,int right,int[] temp){
int i = left;//Initial index of right ordered sequence
int j = mid + 1;//Initialize j, initial index of right ordered sequence
int t = 0;//Current index of temp array
//(1)
//Fill the left and right (ordered) data into the temp array as a rule first
//Until one side of the ordered sequence is processed
while (i <= mid && j <= right){//Continue
//If the current element of the left ordered sequence is less than or equal to the current element of the right ordered sequence
//Copy the current element on the left to the temp array
//Then t++, i+.
if(arr[i] <= arr[j]){
temp[t] = arr[i];
t += 1;
i += 1;
} else{//Instead, fill the current element of the right ordered sequence into the temp array
temp[t] = arr[j];
t += 1;
j += 1;
}
}
//(2)
//Fill temp with data from one side of the remaining data in turn
while (i <= mid){//Ordered sequence on left with remaining elements, all filled to temp
temp[t] = arr[i];
t += 1;
i += 1;
}
while (j <= right){
temp[t] = arr[j];
t += 1;
j += 1;
}
//(3)
//Copy elements of temp array to arr
t = 0;
int tempLeft = left;
while (tempLeft <= right){//First merge tempLeft
arr[tempLeft] = temp[t];
t += 1;
tempLeft += 1;
}
}
//Division+Combination Method
public static void mergeSort(int[] arr,int left,int right,int[] temp){
if(left < right){
int mid = (left + right) / 2; //Intermediate Index
//Decomposition recursively to the left
mergeSort(arr,left,mid,temp);
//Decomposition Recursively Right
mergeSort(arr,mid +1,right,temp);
//merge
merge(arr,left,mid,right,temp);
}
}
}
7. Cardinal Sorting
Cardinal sorting is the implementation of bucket sorting. It assigns sorted elements to some "barrels" by the values in each bit of the key value, cuts integers into different numbers by bits, and compares them by bits to achieve the sorting effect. The cardinality sorting method is a stable sorting method, and the cardinality sorting method is an efficient and stable sorting method.
The basic idea of cardinality ordering is to unify all the values to be compared into the same number of digits, with the shorter digits preceded by zeros. Then, start with the lowest bit and sort one by one. In this way, the sequence becomes an ordered sequence from the lowest to the highest.
public class RadixSort {
public static void main(String[] args) {
// int arr[] = { 53, 3, 542, 748, 14, 214};
// 80000000 * 11 * 4 / 1024 / 1024 / 1024 =3.3G
int[] arr = new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i] = (int) (Math.random() * 80000);
}
long begin = System.currentTimeMillis();
radixSort(arr);
long end = System.currentTimeMillis();
System.out.println((double) (end - begin) / 1000 + "s");
// for (int i : arr) {
// System.out.print(i + " ");
// }
}
public static void radixSort(int[] arr) {
int max = arr[0];
for(int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
int maxLength = (max + "").length();
int[][] bucket = new int[10][arr.length];
int[] bucketElementCounts = new int[10];
for(int i = 0 , n = 1; i < maxLength; i++, n *= 10) {
for(int j = 0; j < arr.length; j++) {
int digitOfElement = arr[j] / n % 10;
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
bucketElementCounts[digitOfElement]++;
}
int index = 0;
for(int k = 0; k < bucketElementCounts.length; k++) {
if(bucketElementCounts[k] != 0) {
for(int l = 0; l < bucketElementCounts[k]; l++) {
arr[index++] = bucket[k][l];
}
}
bucketElementCounts[k] = 0;
}
}
}
}
8. Summary and comparison of common sorting algorithms
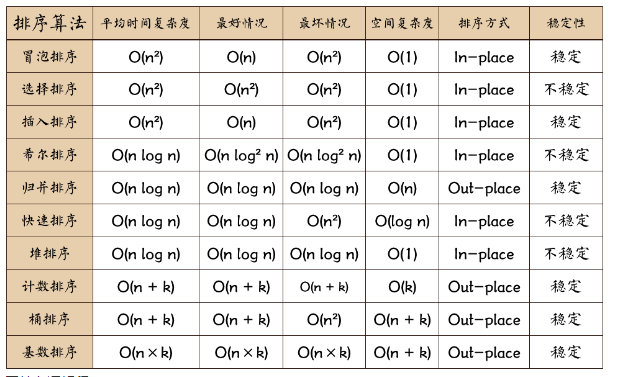
Interpretation of related terms:
Stability: if a was originally in front of B and a=b, a would still be in front of B after sorting;
Unstable: if a is before B and a=b, a may appear after B after sorting;
Internal sorting: All sorting operations are done in memory;
Outside sorting: Because the data is too large, the data is placed on disk, and sorting can only be done by data transfer from disk and memory;
Time Complexity: The time it takes an algorithm to execute.
Spatial Complexity: The amount of memory required to run a program.
n: Data size
k: Number of buckets
In-place: Does not consume extra memory
Out-place: Extra memory usage