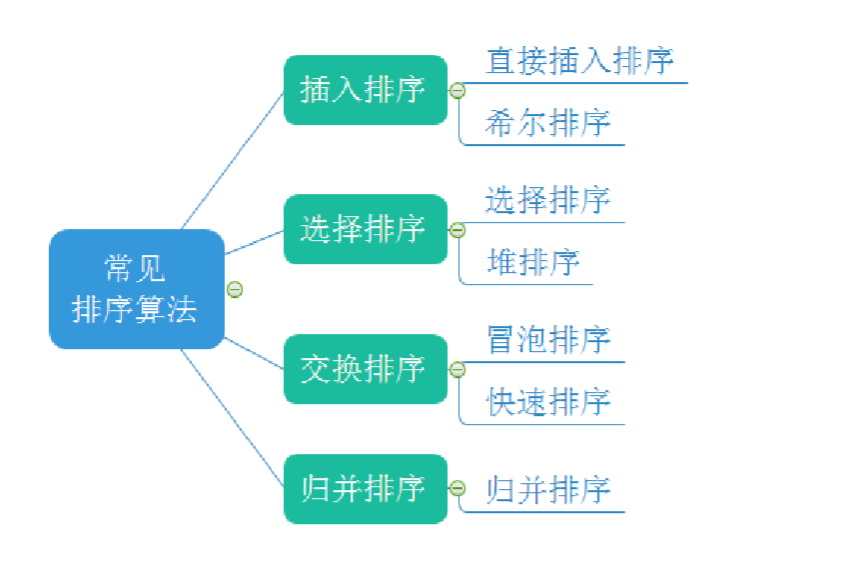
Direct insert sort

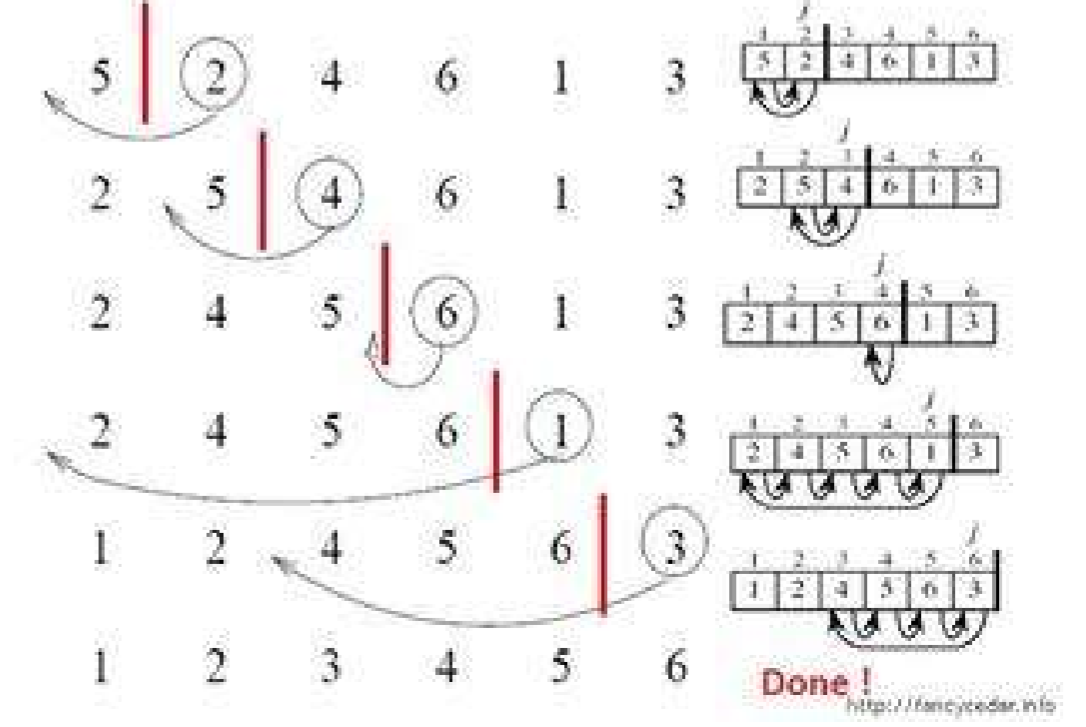
When the I (I > = 1) element is inserted, the preceding array[0],array[1] , array[i-1] has been ordered. At this time, use the sorting code of array[i] and array[i-1],array[i-2] By comparing the order of sorting codes, find the insertion position, i.e. insert array[i], and move the order of elements in the original position backward

1. The closer the set of elements is to order, the more efficient the direct insertion sorting algorithm is
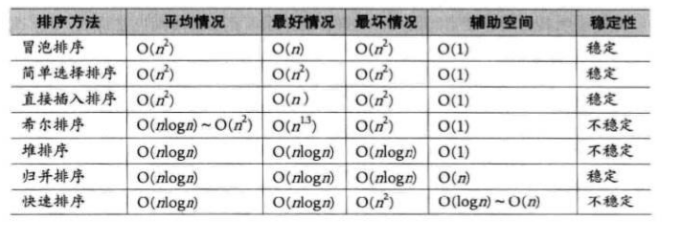
2. Time complexity: O(N^2)
3. Spatial complexity: O(1), which is a stable sorting algorithm
4. Stability: stable

//The order is like playing cards. When you get a card, the cards are in order,
//Compared with the biggest card in hand, when you know that it is bigger than other cards, insert
private void insertSort(int[] array) {
    for (int i = 1; i < array.length; i++) {
        int tmp = array[i];       //Draw cards
        int j;
        for (j = i - 1; j >= 0 ; j--) {  // Compare from the last one
            if (array[j] > tmp){
                array[j + 1] = array[j];  //If the current card is larger than the drawn card, move one backward
            }else {
                break;      // Until bigger than the current card, jump out of the loop
            }
        }
        array[j + 1] = tmp;  // Insert after current position
    }
}

Selection sort

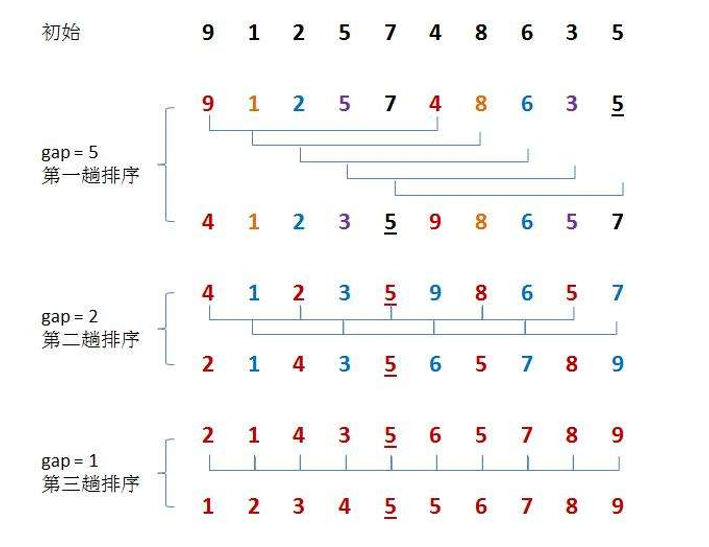
The basic idea of hill sorting method is to select an integer first, divide all records in the file to be sorted into groups, divide all records with a distance into the same group, and sort the records in each group. Then, take and repeat the above work of grouping and sorting. When = 1 is reached, all records are ordered in a unified group.

private void shellSort(int[] array) {
    int[] gap = {5,3,1};
    for (int i = 0; i < gap.length; i++) {
        shell(array,gap[i]);
    }
}

private void shell(int[] array, int gap) {
    for (int i = gap; i < array.length; i++) {
        int tmp = array[i];
        int j;
        for (j = i - gap; j >= 0; j -= gap) {
            if(array[j] > tmp){
                array[j + gap] = array[j];
            }else {
                break;
            }
        }
        array[j + gap] = tmp;
    }
}

Summary of the characteristics of hill sorting:

1. Hill sort is an optimization of direct insertion sort.
2. When gap > 1, they are all pre ordered, in order to make the array closer to order. When gap == 1, the array is almost ordered, so it will be very fast. In this way, the overall effect of optimization can be achieved. After implementation, we can compare the performance test.
3. The time complexity of hill sorting is not easy to calculate, so it needs to be derived, and the average time complexity is derived:
   O(N1.3—N2)
4. Stability: unstable

Selection sort

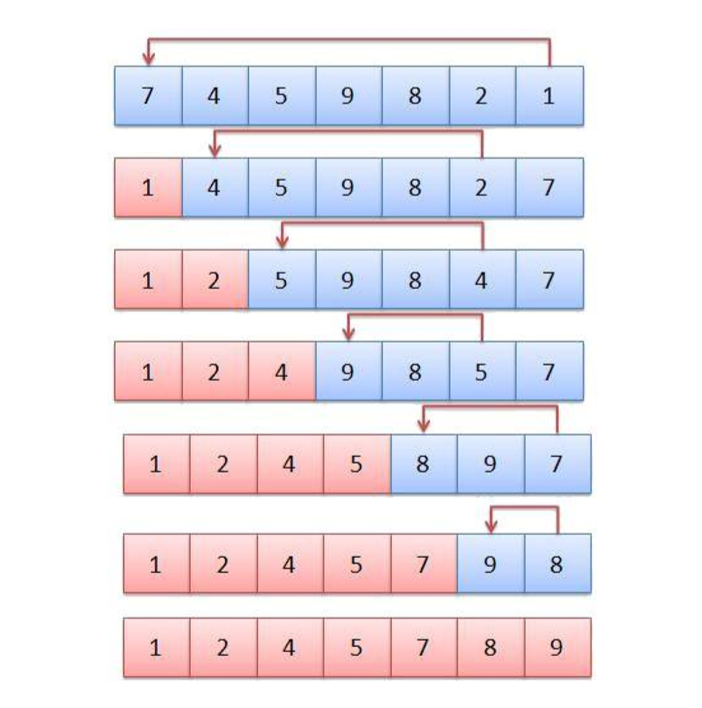
Each time, select the smallest (or largest) element from the data elements to be sorted, and store it at the beginning of the sequence until all the data elements to be sorted are finished.

private void selectSort(int[] array) {
    for (int i = 0; i < array.length; i++) {
        for (int j = i + 1; j < array.length; j++) {
            if (array[i] > array[j]){
                int tmp = array[i];
                array[i] = array[j];
                array[j] = tmp;
            }
        }
    }
}

1. It's easy to understand how to think by direct selection and sorting, but the efficiency is not very good. Rarely used in practice
2. Time complexity: O(N^2)
3. Space complexity: O(1)
4. Stability: unstable

Bubble sort

The so-called exchange is to exchange the positions of the two records in the sequence according to the comparison results of the two record keys in the sequence. The characteristics of exchange sorting are: move the records with larger key values to the tail of the sequence, and the records with smaller key values to the front of the sequence.

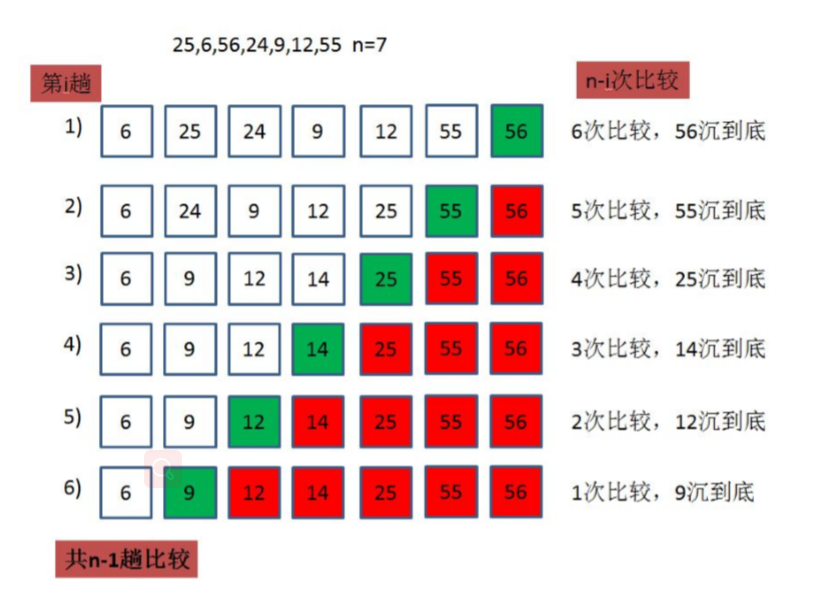
private void bubbleSort(int[] array) {
    for (int i = 0; i < array.length - 1; i++) {
        boolean flag = false;
        for (int j = 0; j < array.length - 1 - i; j++) {
            if (array[j] > array[j+1]){
                int tmp = array[j];
                array[j] = array[j+1];
                array[j+1] = tmp;
                flag = true;
            }
        }
        if (!flag){
            break;
        }
    }
}

Summary of bubble sorting characteristics:

1. Bubble sorting is a very easy to understand sort
2. Time complexity: O(N^2)
3. Space complexity: O(1)
4. Stability: stable

Quick sort

Take any element in the sequence of elements to be sorted as the reference value, and divide the set to be sorted into two subsequences according to the sorting code. All elements in the left subsequence are less than the reference value, and all elements in the right subsequence are greater than the reference value. Then repeat the process in the left and right subsequences until all elements are arranged in corresponding positions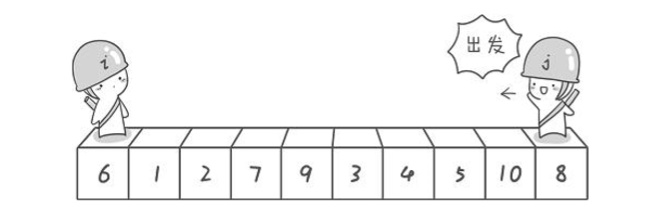

private void quickSort(int[] array) {
    quick(array,0,array.length - 1);
}

private void quick(int[] array, int start, int end) {
    int p = par(array,start,end);
    if (p > start + 1){
        quick(array,start,p - 1);
    }
    if (p < end - 1){
        quick(array,p+1,end);
    }
}

private int par(int[] array, int low, int high) {
    int tmp = array[low];
    while (low < high){
        while(low < high && array[high] >= tmp){
            high--;
        }
        if (low >= high){
            break;
        }else {
            array[low] = array[high];
        }
        while(low < high && array[low] <= tmp){
            low++;
        }
        if (low >= high){
            break;
        }else {
            array[high] = array[low];
        }
    }
    array[low] = tmp;
    return low;
}

Summary of quick sorting features:

1. The overall comprehensive performance and usage scenarios of quick sorting are relatively good, so we dare to call it quick sorting
2. Time complexity: O(N*logN)
3. Spatial complexity: O(logN)
4. Stability: unstable

Merge sort

By combining the ordered subsequences, we can get the completely ordered sequence, that is, first make each subsequence orderly, then make the subsequence segments orderly. If two ordered tables are combined into one, it is called two-way merge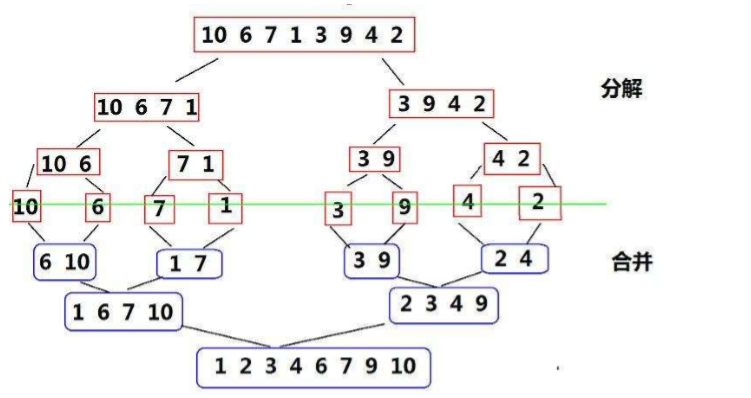

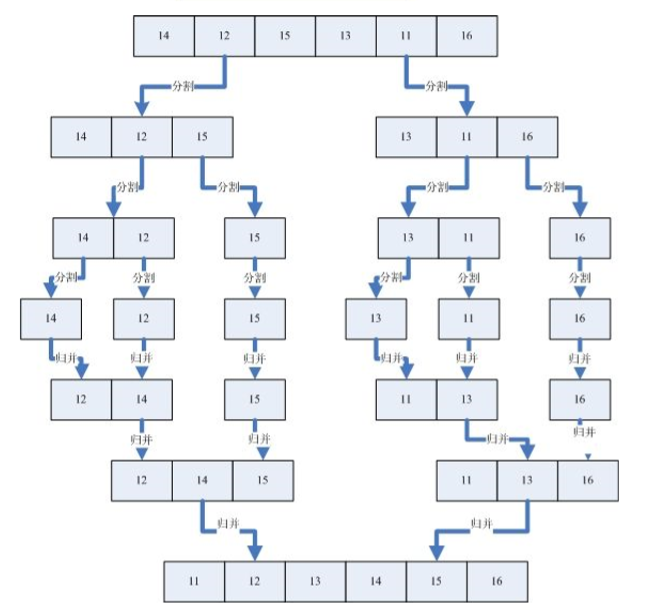
private void mergeSort(int[] array) {
    merge(array,0,array.length - 1,new int[array.length]);
}

private void merge(int[] array, int start, int end, int[] tmpArray) {
    if (start >= end){
        return;
    }
    int mid = (start + end)/2;
    merge(array,start,mid,tmpArray);
    merge(array,mid+1,end,tmpArray);
    //Execute after the left and right full traversal of the current array segment
    merges(array,start,mid,end,tmpArray);
}

private void merges(int[] array, int start, int mid, int end, int[] tmpArray) {
    int index = start;
    int i = start;
    int j = mid + 1;
    while (start <= mid && j <= end){
        if (array[start] <= array[j]){
            tmpArray[index++] = array[start++];
        }else {
            tmpArray[index++] = array[j++];
        }
    }
    while(start <= mid){
        tmpArray[index++] = array[start++];
    }
    while (j <= end){
        tmpArray[index++] = array[j++];
    }
    for (; i <= end; i++) {
        array[i] = tmpArray[i];
    }
}

Summary of characteristics of merging and sorting:

1. The disadvantage of merging is that it needs O(N) space complexity. The thinking of merging and sorting is more to solve the problem of sorting out of disk.
2. Time complexity: O(N*logN)
3. Space complexity: O(N)
4. Stability: stable

Heap sort

Heap sort is a sort algorithm designed by using the data structure of heap tree. It is a kind of selective sort. It selects data through the heap. It should be noted that a large pile should be built in ascending order and a small pile should be built in descending order.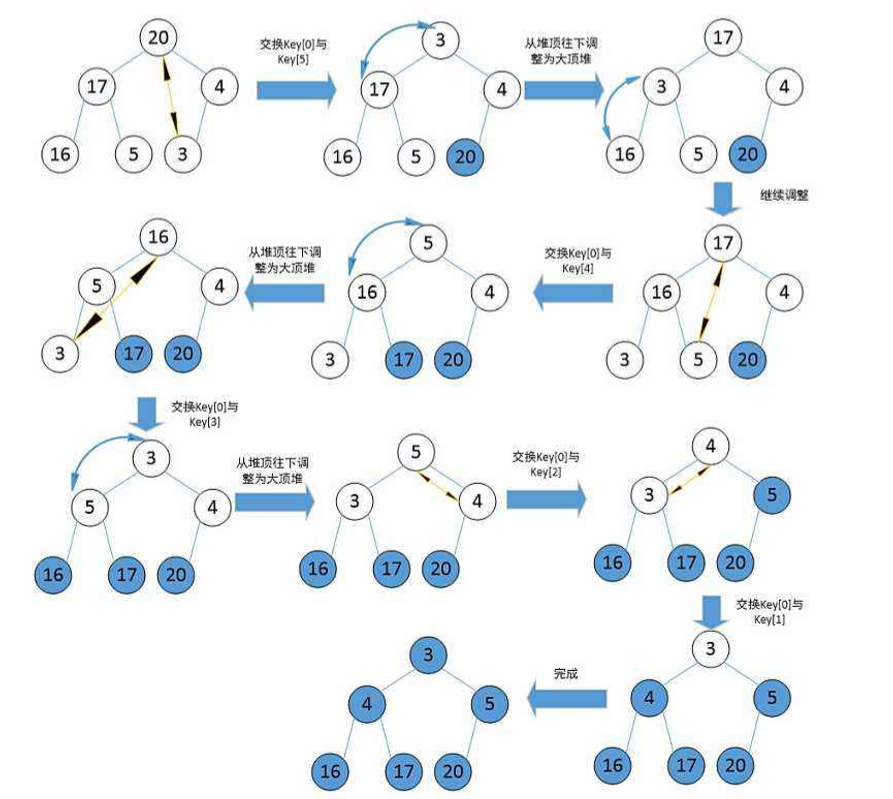

private void heapSort(int[] array) {
    bigHeap(array,array.length);
    for (int i = array.length - 1; i >= 0 ; i--) {
        int tmp = array[i];
        array[i] = array[0];
        array[0] = tmp;
        bigHeap(array,i);
    }
}

private void bigHeap(int[] array, int length) {
    for (int i = (array.length-2)/2; i >= 0 ; i--) {
        AdjustDown(array,i,length);
    }
}

private void AdjustDown(int[] array, int root, int length) {
    int parent = root;
    int child = 2*parent + 1;
    while(child < length){
        if (child  + 1 < length && array[child] < array[child+1]){
            ++child;
        }
        if (array[child] > array[parent]){
            int tmp = array[child];
            array[child] = array[parent];
            array[parent] = tmp;
            parent = child;
            child = 2*parent + 1;
        }else {
            break;
        }
    }
}

A summary of the characteristics of heap sorting:

1. Heap sorting uses heap to select data, which is much more efficient.
2. Time complexity: O(N*logN)
3. Space complexity: O(1)
4. Stability: unstable