1, dijkstra algorithm

The single source shortest path algorithm has the lowest complexity among the four basic shortest path algorithms, but it is not suitable for graphs with negative weight edges. Greedy thought, from the beginning to the end, a layer of ergodic graph. The shortest path from the starting point to any point can be found. The idea is a bit like prim (minimum spanning tree algorithm)

1. Algorithm:

First set up two sets, S and Q. The S set is used to store the shortest path point that has been determined, and the Q set is used to store the undetermined point.

Next, we use dist [] array to represent the distance from the starting point to each point.

Then start the demonstration:
First, you have a map (how to build a map is determined according to the meaning of the topic)

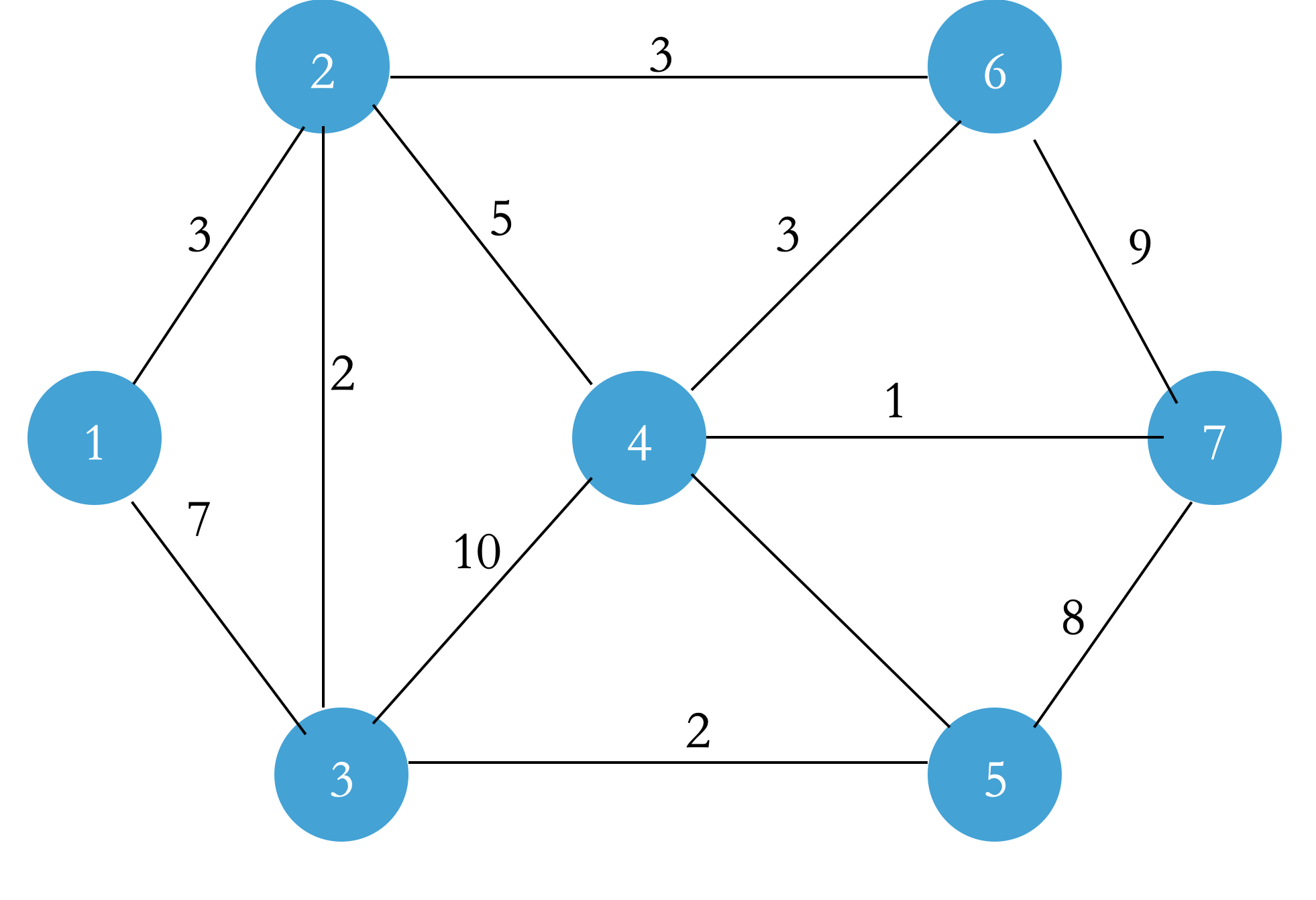
The path distance of all points is set to ∞, that is, dist[1 ~ n] = ∞. The dist[1] of the starting point is updated to 0 (this is the distance from your home to your home!);

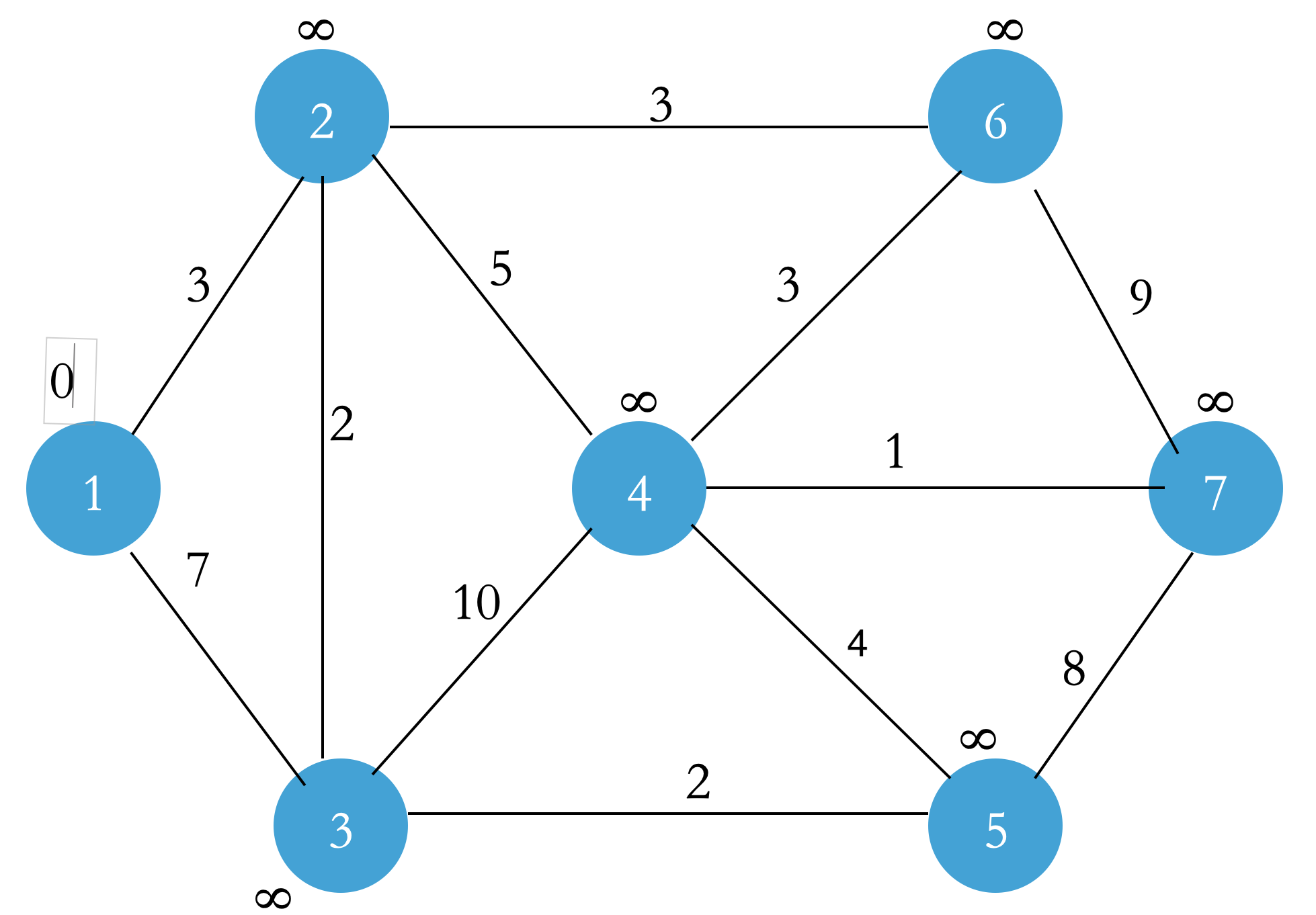
Update the point linked by the first point in the Q set: to update the point dist = min (dist of the point, dist + edge weight of the first point) (relaxation operation), and add the first point to the S set;

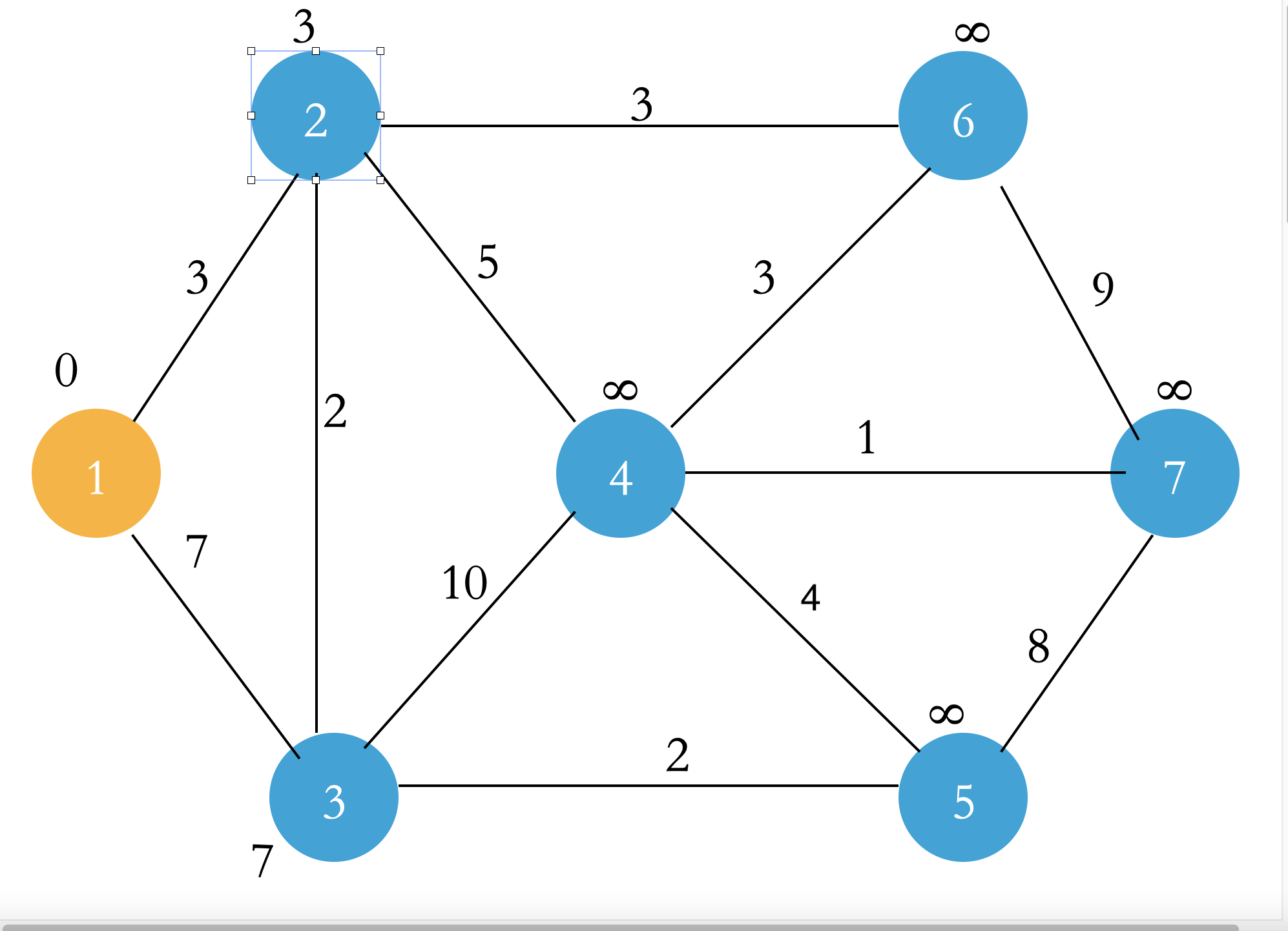
Select the point u with the smallest dist in the Q set. Let the points connected to point u and not in the S set and point u relax, and add point u to the S set. Then repeat this step until all points enter the S set.

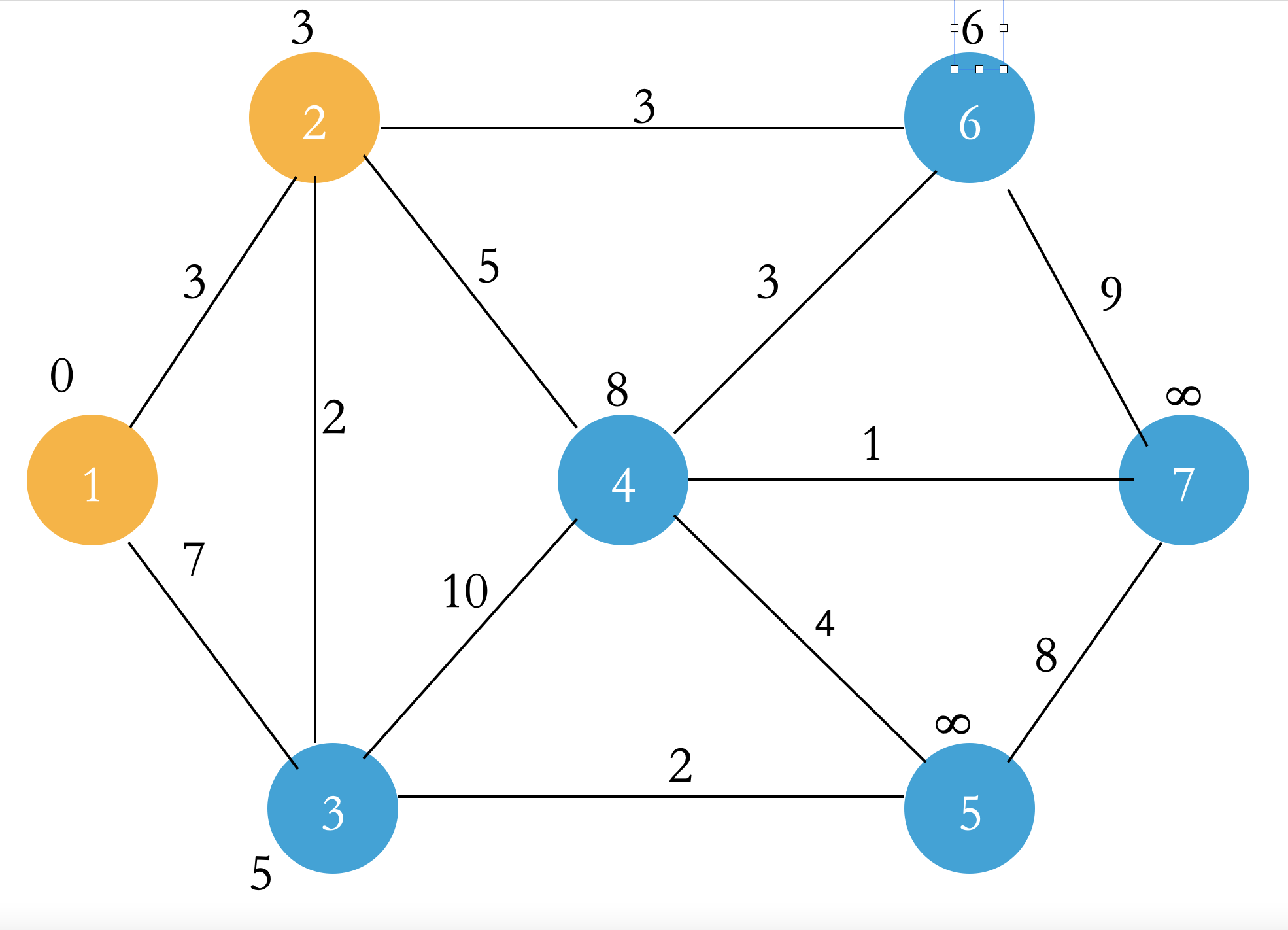
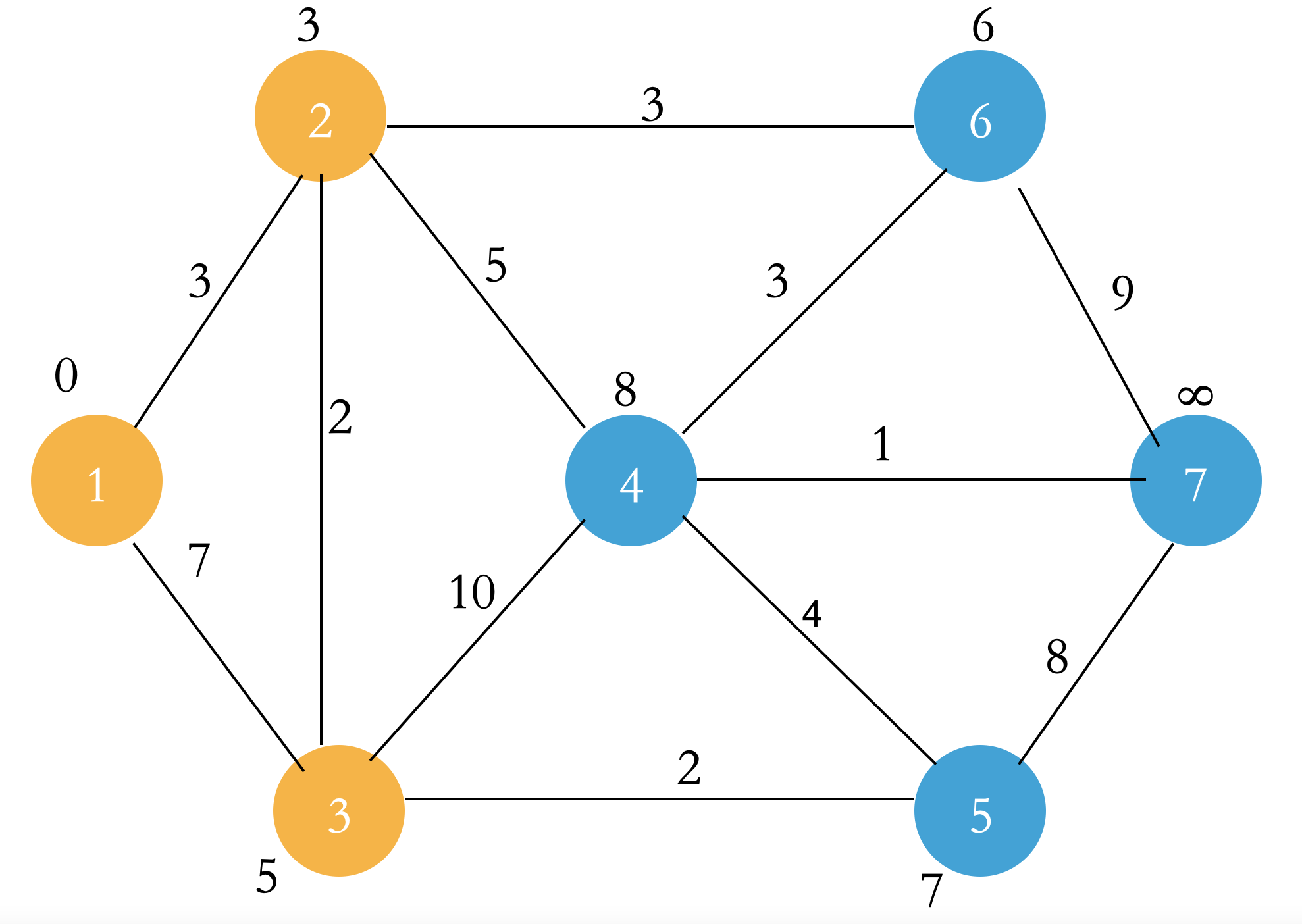
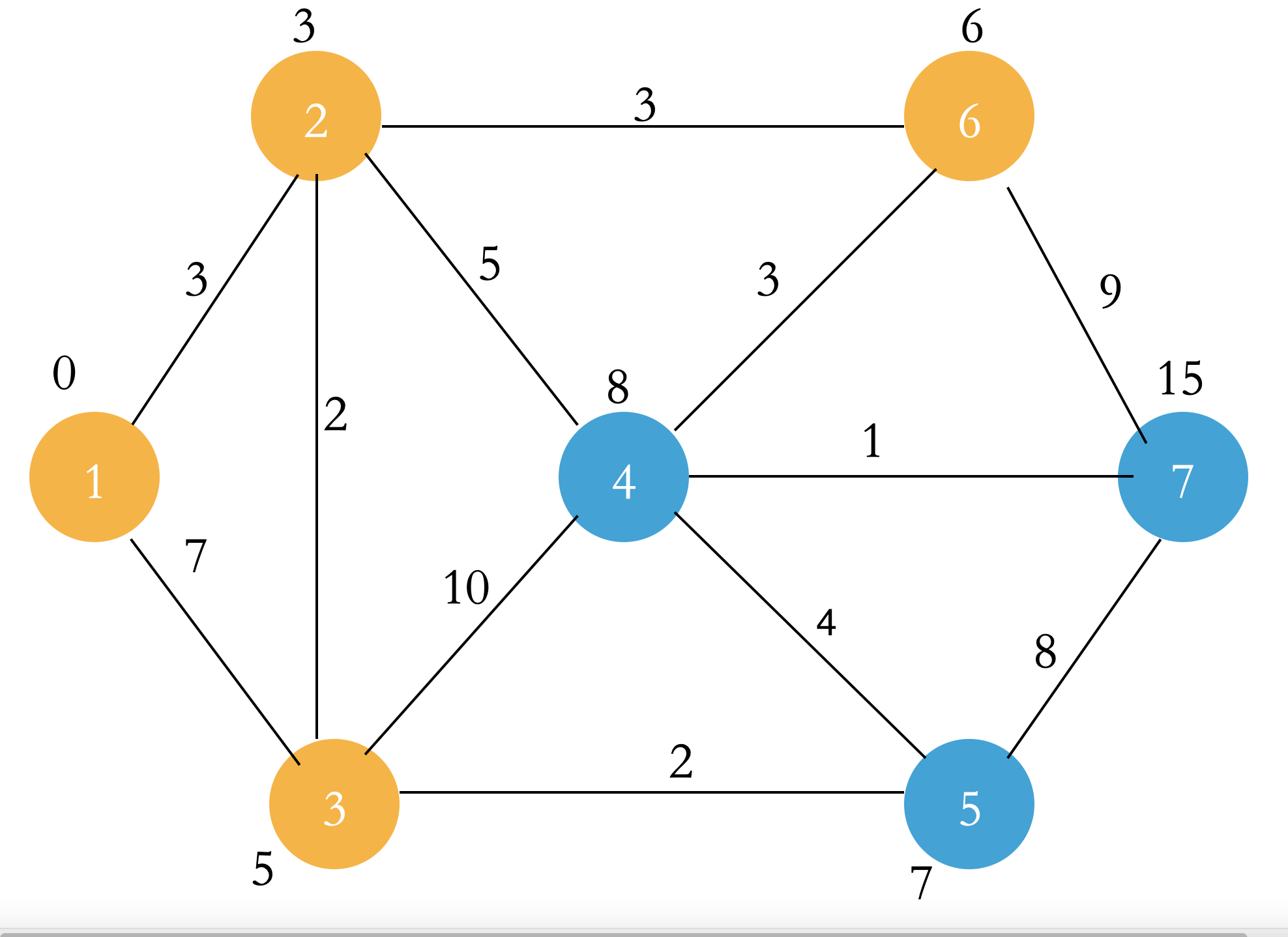
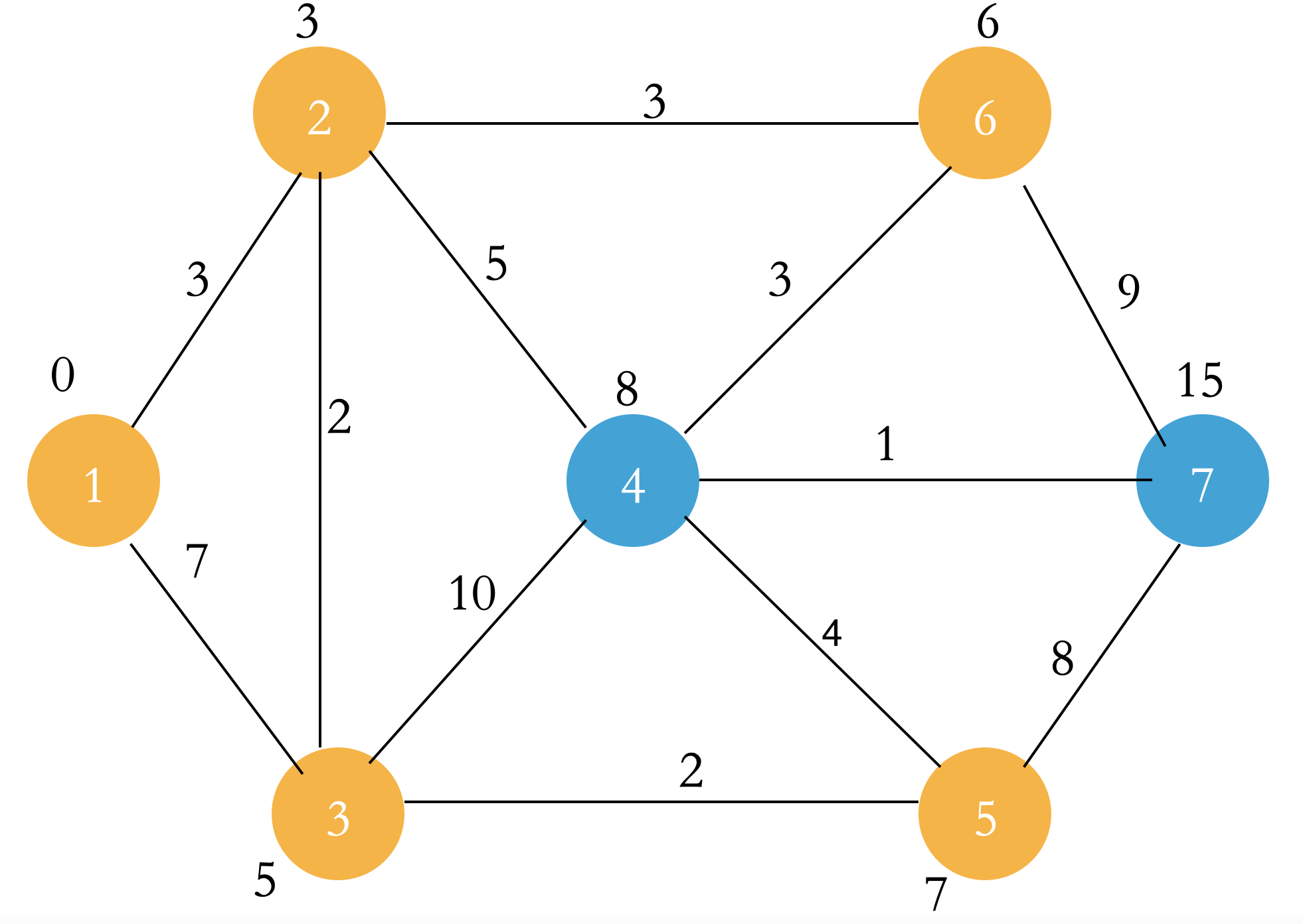
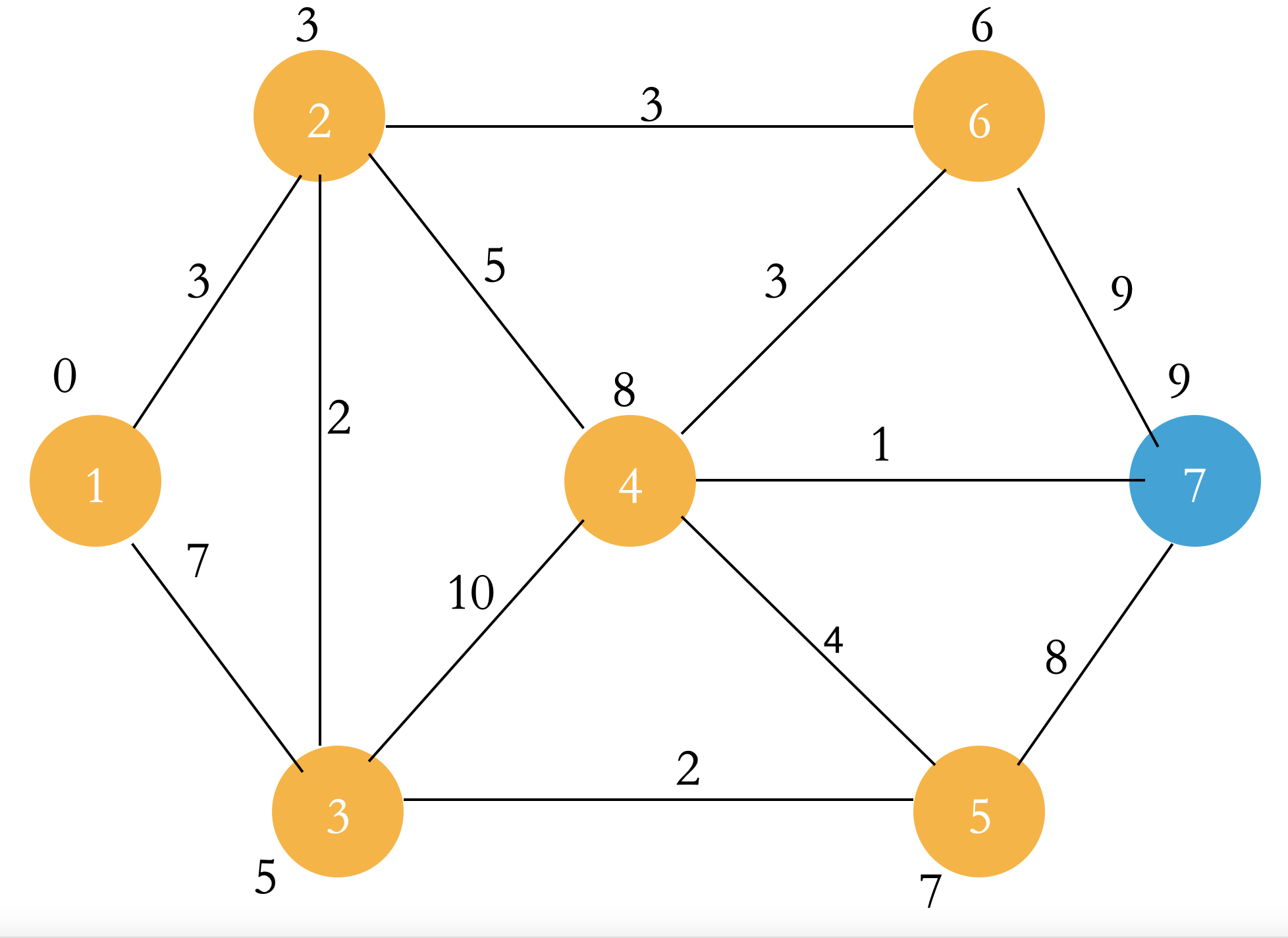
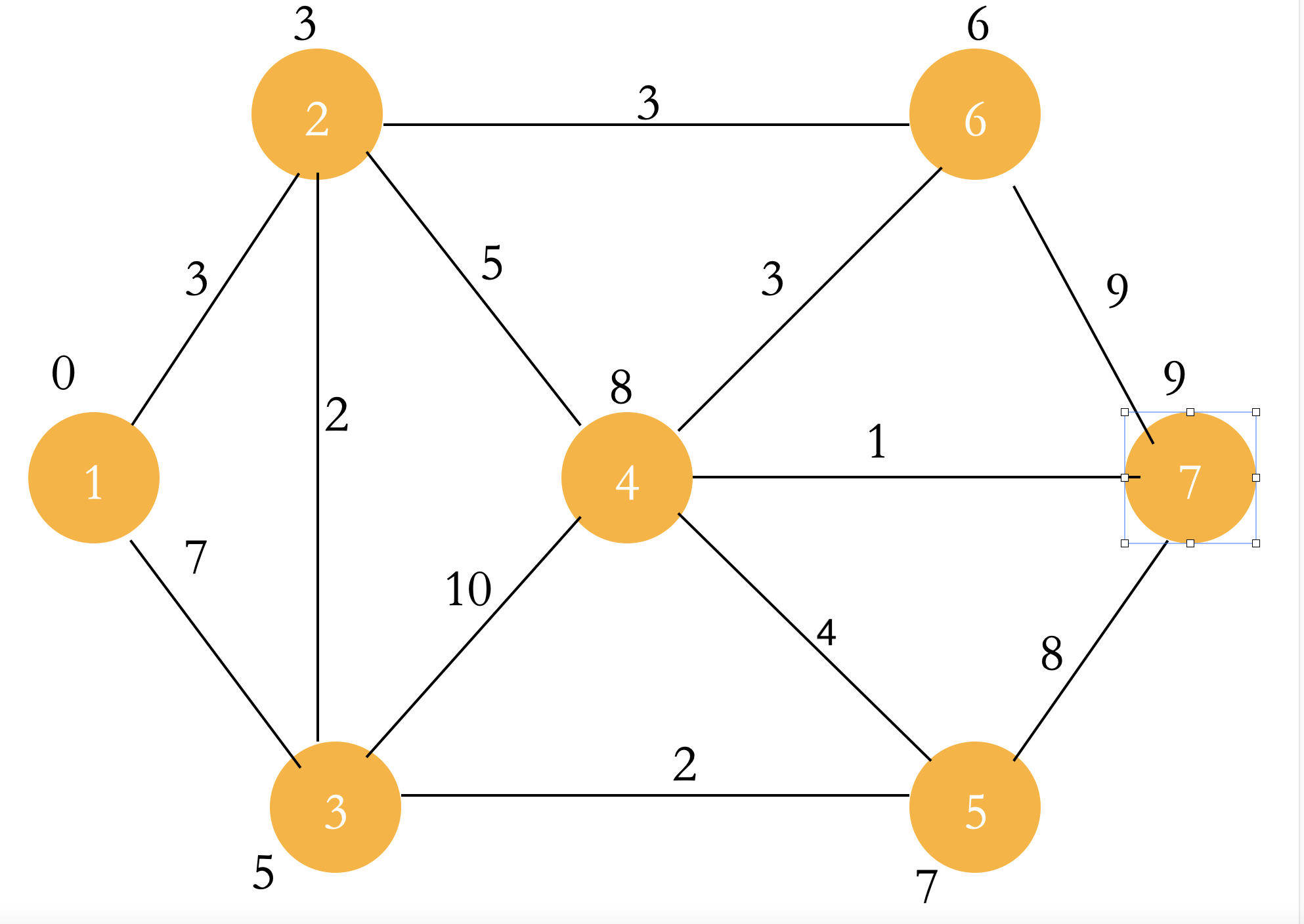
When all steps are completed, the dist of the point in the figure is the shortest path from the starting point to each point!

Thought:

Update layer by layer, and select the point closest to the point in the S set each time to enter the S set

2. Code implementation

#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
typedef long long int ll;
const int N = 1e5+7;
const int INF = 1e9;
struct one_tu//Chain forward star construction map
{
    int v, w, next;
}tu[N];
int head[N],top,n,m;
void build(int u,int v,int w)
{
    top ++;
    tu[top] = {v, w, head[u]};
    head[u] = top;
}

struct node//Set up a priority queue
{
    bool friend operator < (node a, node b)
    {
        return a.cost > b.cost;//Sort by cost from small to large (overload is the opposite)
    }
    ll cost, to;//Cost - > distance and to - > point stored in the queue
};
int dist[N];//Distance, used to save the distance from the starting point to the change point
bool jud[N];//Judge whether to enter S queue

void dijkstra(int s)//dijkstra algorithm 
{
    priority_queue <node> q;//Establish priority queue
    for(int i = 1; i <= n; i++)
    {
        dist[i] = INF;//Update maximum
        jud[i] = false;//Tag data update
    }
    dist[s] = 0;
    q.push({0,s});//Initial point join the team
    while(!q.empty())
    {
        ll u = q.top().to;
        q.pop();
        if(jud[u])continue;
        jud[u] = true;//Add point u to S set
        for(int i = head[u]; i; i = tu[i].next)
        {
            int v = tu[i].v, w = tu[i].w;
            if(dist[v] > dist[u] + w)//Slack operation
            {
                dist[v] = dist[u] + w;
                if(!jud[v])//Judge whether point v is in the team
                    q.push({dist[v],v});//Point v join the team
            }
        }
    }
}
//dist[N] array will finally represent the shortest path from the starting point to 1 ~ n points
int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 0; i <= m; i++)
    {
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        build(u,v,w);//Mapping
    }
    dijkstra(1);
    
    printf("%d",dist[n]);
    return 0;
}

2, Description of some problems

1. Why dijkstra can't we seek the path with negative weight!

Because the negative weight path may have a negative ring, dijkstra will make mistakes, but it is only wrong, and there will be no cycle of life and death. Unless the code is wrong!!
Let's start with a diagram:

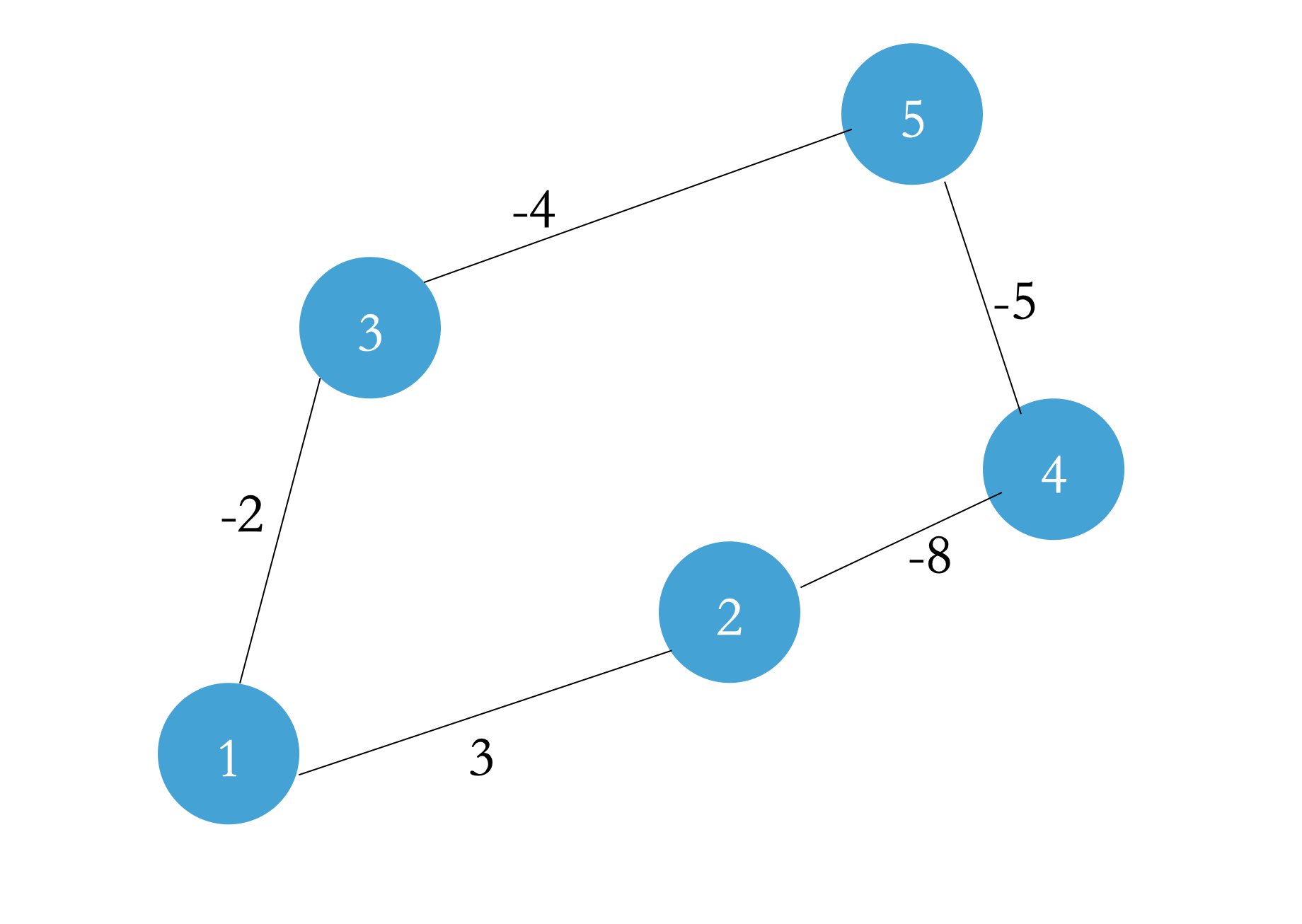
In this figure, you can easily find that if you run according to dijkstra algorithm, it will display dist[5] = -6; But in fact, dist[5] = -10, dist[5] = - ∞. In fact, as long as you run a few more laps, his value will become smaller and smaller, so you can run - ∞;

2. If there is no negative ring, but there is a negative weighted edge, is that ok?

The answer is yes. It doesn't affect dijkstra's running method. However, if you want to test whether it has a negative loop, why not use the algorithm to run its shortest path!

3. If there are negative weight edges on the graph, can I subtract the minimum edge weight from all the edge weights?

Answer: no! Come on, picture above, just a picture!

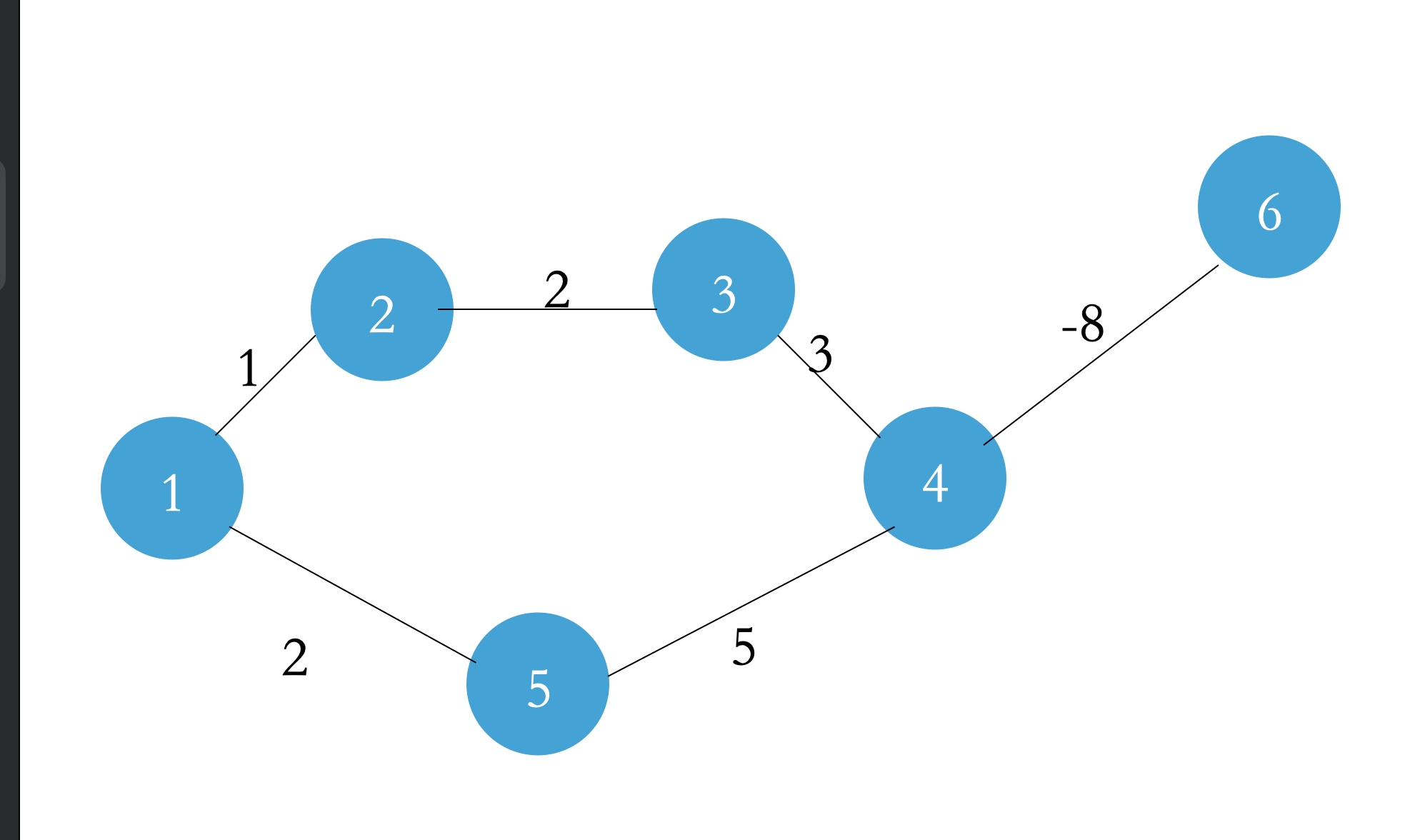
For this graph, if you want to add all the edge weights to the same value, it will lead to the shortest path, not the previous one!
Each edge weight - (- 8) so
Original shortest path: the edge weight of 1 - > 2 - > 3 - > 4 will be + 24, and the total edge weight will become 30;
However, the new shortest path is: 1 - > 5 - > 4 edge weights. After updating, the total edge weights will be 7 + 16 = 23;
That's it! He can't

4. What if I want to run a graph with negative weight with dijkstra

There's a way! For details, see: Johnson
I wrote this by myself. It's mainly the idea above. It's really good!