What is signed distance field (SDF)?
Signed distance field (SDF) refers to the establishment of a spatial field in which each pixel or voxel records its distance from the surrounding pixels or voxels. If it is inside the object, the distance bit is negative. If it is outside, the distance of the difference is recorded, and the bit on the edge is just 0
The demonstration on 2D is as follows
Original drawing:

SDF

In short, it is an information recording spatial distance.
What can SDF do?
1. High definition text (TMP)
2. Deformation animation
3. Sequence frame animation is too soft
4. Collision detection
5. Soft shadow
6. Environmental shelter (AO)
TMP:
People who have used TMP may have the impression that he is a friendly distance text, and his own picture information records his distance field.

GPU determines the information of intermediate points by interpolation
For bitmaps, each pixel is RGB color, and the interpolation of the surrounding values has no practical significance. (a mixture of Mathematics).
However, for SDF, each pixel is the directional distance of the boundary, and the new points are obtained after interpolation. SDF uses the characteristics of interpolator to realize the smooth amplification effect.
In this step, you only need to record the image of the signed distance field, and then interpolate in the shader.
for instance:
fixed4 sdf = tex2D(_SDFTextTexture, i.uv); float distance = sdf.a; col.a = smoothstep(_DistanceMark - _SmoothDelta, _DistanceMark + _SmoothDelta, distance); col.rgb = lerp(fixed3(0,0,0), fixed3(1,1,1), col.a);
Deformation animation:

This is composed of two signed distance field data

Then a simple Lerp operation is performed in the sampling of two distance field textures (remember linear space, do not compress the texture).
Sequence frame animation is too soft:
Its implementation principle is to sample one more frame in the sequence frame of signed distance field, and then make time transition between the two frames.

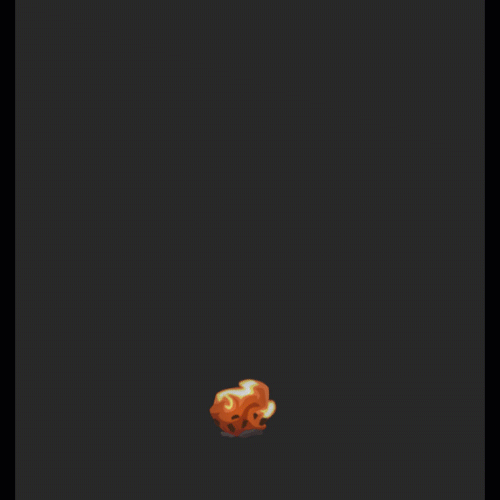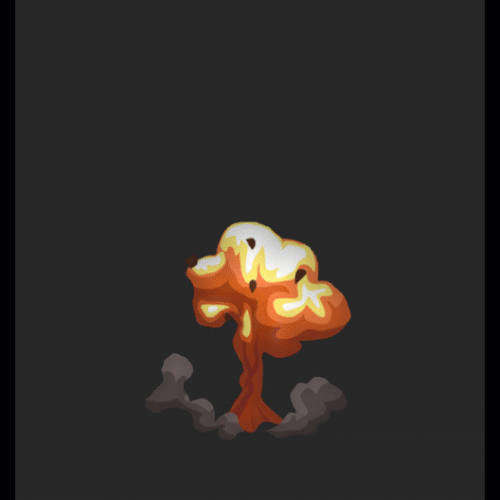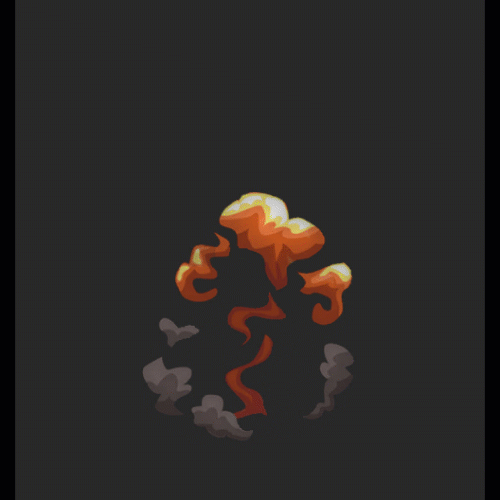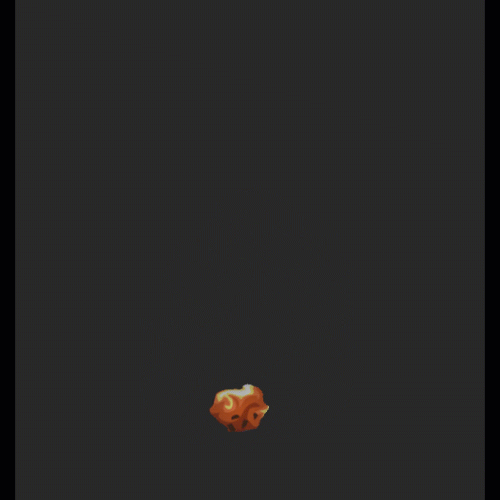
Collision detection:
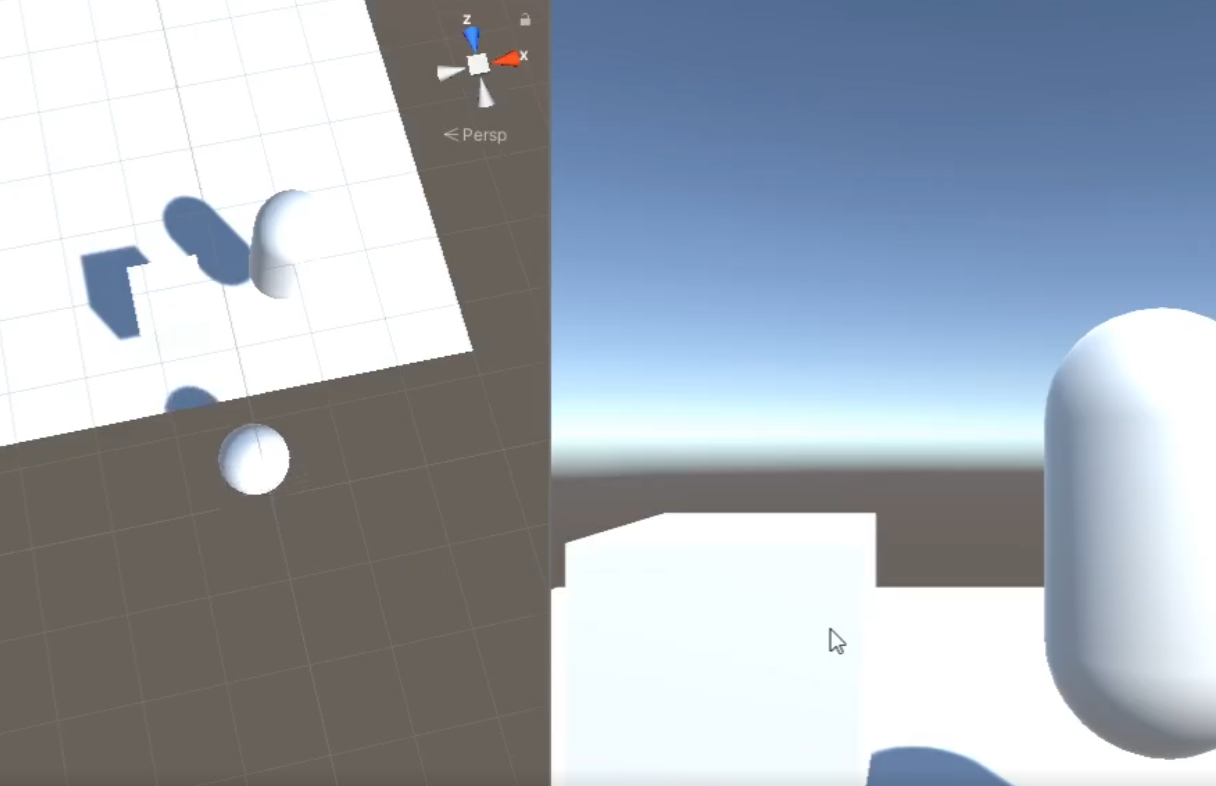
The implementation process of this can be described in detail:
First, establish a signed distance field:
for (int i = -half; i < half; i++)
{
for (int j = -half; j < half; j++)
{
for (int k = -half; k < half; k++)
{
bool isContinue = false;
for (int q = 0; q < SDFCollider.Length; q++)
{
Vector3 origin = new Vector3(i, j, k);
Vector3Int vector = new Vector3Int(Mathf.RoundToInt(i * floatToIntNum), Mathf.RoundToInt(j * floatToIntNum), Mathf.RoundToInt(k * floatToIntNum));
Vector3 dir = (SDFCollider[q].transform.position - origin).normalized;
Ray ray = new Ray(origin, dir);
if (Physics.Raycast(ray, 1f))
{
SubSDF(new Vector3(i, j, k), SDFCollider);
isContinue = true;
continue;
}
AddSDFData(vector, ray);
}
if (isContinue)
{
continue;
}
}
}
}The method here is to detect whether the emitted ray hits the object surface between - half and half according to the center of all collider s of sdfcollier. If not, record the distance. (note that ijk is incremented by int, which means I use 1 as a prime.).
If there is a collision with the surface, it means that there is a collision body here, and the collision body needs to be refined. Here, I continue to detect the finer distance field in SubSDF.
private void SubSDF(Vector3 startVector, Transform[] trans)
{
float interval = 0.1f;
for (float i = startVector.x-1; i <= startVector.x + 1; i+= interval)
{
for (float j = startVector.y-1; j <= startVector.y + 1; j += interval)
{
for (float k = startVector.z-1; k <= startVector.z + 1; k += interval)
{
bool isContinue = false;
for (int q = 0; q < trans.Length; q++)
{
Vector3 origin = new Vector3(i, j, k);
Vector3Int vector = new Vector3Int(Mathf.RoundToInt(i * floatToIntNum), Mathf.RoundToInt(j * floatToIntNum), Mathf.RoundToInt(k * floatToIntNum));
Vector3 dir = (trans[q].transform.position - origin).normalized;
Ray ray = new Ray(origin, dir);
if (Physics.Raycast(ray, (interval + 0.1f)))
{
AddSDF(vector, -1);
isContinue = true;
continue;
}
AddSDFData(vector, ray);
}
if (isContinue)
{
continue;
}
}
}
}
}In SubSDF, I will step by step to find collision points with an interval of 0.1. If there are collision points, AddSDFData will be added to the sdf data.
The tree data structure is used here, which is equivalent to taking 1 as the step if there is no collision data. If there is collision data, it indicates that there is a collision body within 1 meter, and it is refined to 0.1 meter as the step.
If you visually look at the boundaries covered by these signed distance fields, you can see something like this
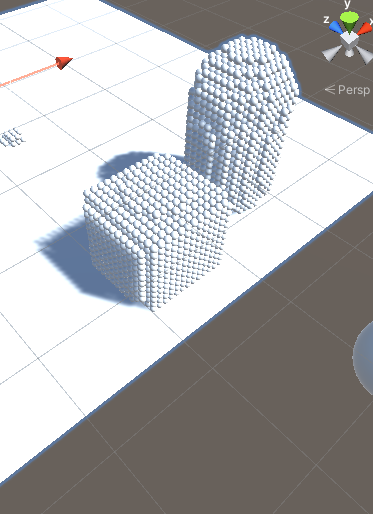
Signed distance field detection:
There are two ways to detect:
The first is relatively simple. According to the number of collision bodies, traverse, and then subtract their center from the center of the current point as the direction, and then step here. If the step distance has distance field data and its value is less than 0, it means that he has collided with the edge and won't let him go.
for (int i = 0; i < SDFCreator.SDFCollider.Length; i++)
{
Vector3 radius = (SDFCreator.SDFCollider[i].transform.position - this.transform.position).normalized * 0.4f;
Vector3 newPos = this.transform.position;
Vector3 circle = newPos + radius;
Vector3Int vector = new Vector3Int(Mathf.RoundToInt(circle.x * SDFCreator.floatToIntNum), Mathf.RoundToInt(circle.y * SDFCreator.floatToIntNum), Mathf.RoundToInt(circle.z * SDFCreator.floatToIntNum));
if (SDFCreator.mSDFValue.ContainsKey(vector))
{
//Debug.Log("distance:" + SDFCreator.mSDFValue[vector]);
if (SDFCreator.mSDFValue[vector] < 0)
{
//Debug.LogError("hit");
this.transform.position -= pos;
break;
//Vector3 normalDir =
}
}
}The second is more complex. It is more applicable to the case of more collision bodies, but it will also increase additional memory. That is, the octree is used to record the area where the current signed distance field is.
The specific judgment is to go down layer by layer until the smallest unit has collision data, indicating that it is a collision.
The code to create a field and move is:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class SDFCreator : MonoBehaviour
{
public static Dictionary<Vector3Int, float> mSDFValue = new Dictionary<Vector3Int, float>();
public int TotalNum = 50;
public const float floatToIntNum = 10.0f;
public static Transform[] SDFCollider;
// Start is called before the first frame update
void Start()
{
CreateSDF();
//ShowSDF();
RemoveCollider();
}
private void AddSDF(Vector3Int vector, float value)
{
if (mSDFValue.ContainsKey(vector))
{
if (value < mSDFValue[vector])
{
mSDFValue[vector] = value;
}
}
else
{
mSDFValue.Add(vector, value);
}
}
private void ShowSDF()
{
foreach(var sdf in mSDFValue)
{
if (sdf.Value < 0)
{
GameObject go = GameObject.CreatePrimitive(PrimitiveType.Sphere);
Component.Destroy(go.GetComponent<Collider>());
go.transform.SetParent(this.transform);
go.transform.position = new Vector3((float)sdf.Key.x / floatToIntNum, (float)sdf.Key.y / floatToIntNum, (float)sdf.Key.z / floatToIntNum);
go.transform.localScale = new Vector3(0.1f, 0.1f, 0.1f);
}
}
}
private void SubSDF(Vector3 startVector, Transform[] trans)
{
float interval = 0.1f;
for (float i = startVector.x-1; i <= startVector.x + 1; i+= interval)
{
for (float j = startVector.y-1; j <= startVector.y + 1; j += interval)
{
for (float k = startVector.z-1; k <= startVector.z + 1; k += interval)
{
bool isContinue = false;
for (int q = 0; q < trans.Length; q++)
{
Vector3 origin = new Vector3(i, j, k);
Vector3Int vector = new Vector3Int(Mathf.RoundToInt(i * floatToIntNum), Mathf.RoundToInt(j * floatToIntNum), Mathf.RoundToInt(k * floatToIntNum));
Vector3 dir = (trans[q].transform.position - origin).normalized;
Ray ray = new Ray(origin, dir);
if (Physics.Raycast(ray, (interval + 0.1f)))
{
AddSDF(vector, -1);
isContinue = true;
continue;
}
AddSDFData(vector, ray);
}
if (isContinue)
{
continue;
}
}
}
}
}
private void AddSDFData(Vector3Int vector, Ray ray)
{
RaycastHit[] hits = Physics.RaycastAll(ray);
if (hits.Length > 0)
{
float minDistance = 10000;
foreach (var hit in hits)
{
minDistance = Mathf.Min(hit.distance, minDistance);
}
AddSDF(vector, minDistance);
}
}
public void CreateSDF()
{
SDFCollider = this.GetComponentsInChildren<Transform>();
int half = TotalNum / 2;
for (int i = -half; i < half; i++)
{
for (int j = -half; j < half; j++)
{
for (int k = -half; k < half; k++)
{
bool isContinue = false;
for (int q = 0; q < SDFCollider.Length; q++)
{
Vector3 origin = new Vector3(i, j, k);
Vector3Int vector = new Vector3Int(Mathf.RoundToInt(i * floatToIntNum), Mathf.RoundToInt(j * floatToIntNum), Mathf.RoundToInt(k * floatToIntNum));
Vector3 dir = (SDFCollider[q].transform.position - origin).normalized;
Ray ray = new Ray(origin, dir);
if (Physics.Raycast(ray, 1f))
{
SubSDF(new Vector3(i, j, k), SDFCollider);
isContinue = true;
continue;
}
AddSDFData(vector, ray);
}
if (isContinue)
{
continue;
}
}
}
}
}
private void RemoveCollider()
{
foreach (var c in SDFCollider)
{
Component.Destroy(c.GetComponent<Rigidbody>());
Component.Destroy(c.GetComponent<Collider>());
}
}
private void Update()
{
if (Input.GetKey(KeyCode.Space))
{
OCTree();
}
}
public struct ocTree
{
public Vector3 startPos;
public float Len;
}
private void OCTree()
{
int half = TotalNum / 2;
CreateOCTree(-half, 0, -half, 0, -half, 0, half, 1);
}
private Dictionary<int, List<ocTree>> mOCTrees = new Dictionary<int, List<ocTree>>();
private void CreateOCTree(float left, float right, float top, float bottom, float front, float back, float len, int index, bool isAddIndex = true)
{
int nextIndex = index;
if (isAddIndex)
{
nextIndex = index + 1;
}
if (nextIndex >= 10000)
{
return;
}
ocTree lefttopfront = new ocTree();
lefttopfront.startPos = new Vector3(left, top, front);
lefttopfront.Len = len;
ocTree lefttopback = new ocTree();
lefttopback.startPos = new Vector3(left, top, back);
lefttopback.Len = len;
ocTree leftbottomfront = new ocTree();
leftbottomfront.startPos = new Vector3(left, bottom, front);
leftbottomfront.Len = len;
ocTree leftbottomback = new ocTree();
leftbottomback.startPos = new Vector3(left, bottom, back);
leftbottomback.Len = len;
ocTree righttopfront = new ocTree();
righttopfront.startPos = new Vector3(right, top, front);
righttopfront.Len = len;
ocTree righttopback = new ocTree();
righttopback.startPos = new Vector3(right, top, back);
righttopback.Len = len;
ocTree rightbottomfront = new ocTree();
rightbottomfront.startPos = new Vector3(right, bottom, front);
rightbottomfront.Len = len;
ocTree rightbottomback = new ocTree();
rightbottomback.startPos = new Vector3(right, bottom, back);
rightbottomback.Len = len;
List<ocTree> trees = new List<ocTree>();
trees.Add(lefttopfront);
trees.Add(lefttopback);
trees.Add(leftbottomfront);
trees.Add(leftbottomback);
trees.Add(righttopfront);
trees.Add(righttopback);
trees.Add(rightbottomfront);
trees.Add(rightbottomback);
mOCTrees.Add(index, trees);
for (int j = 0; j < trees.Count; j++)
{
Vector3Int vectorStart = new Vector3Int(Mathf.RoundToInt(trees[j].startPos.x * floatToIntNum),
Mathf.RoundToInt(trees[j].startPos.y * floatToIntNum),
Mathf.RoundToInt(trees[j].startPos.z * floatToIntNum));
Vector3Int vectorEnd = new Vector3Int(Mathf.RoundToInt((trees[j].startPos.x + trees[j].Len) * floatToIntNum),
Mathf.RoundToInt((trees[j].startPos.y + trees[j].Len) * floatToIntNum),
Mathf.RoundToInt((trees[j].startPos.z + trees[j].Len) * floatToIntNum));
SubTrees(vectorStart, vectorEnd, nextIndex, trees[j], j);
}
}
private void SubTrees(Vector3Int vectorStart, Vector3Int vectorEnd, int nextIndex, ocTree tree, int nextIndex2)
{
for (int ii = vectorStart.x; ii < vectorEnd.x; ii++)
{
for (int jj = vectorStart.y; jj < vectorEnd.y; jj++)
{
for (int kk = vectorStart.z; kk < vectorEnd.z; kk++)
{
Vector3Int searchPos = new Vector3Int(ii, jj, kk);
if (mSDFValue.ContainsKey(searchPos) && mSDFValue[searchPos] < 0)
{
int cIndex = nextIndex * 10 + (nextIndex2 + 1);
float clen = tree.Len / 2;
float cleft = tree.startPos.x;
float cright = cleft + clen;
float ctop = tree.startPos.y;
float cbottom = ctop + clen;
float cfront = tree.startPos.z;
float cback = cfront + clen;
CreateOCTree(cleft, cright, ctop, cbottom, cfront, cback, clen, cIndex, false);
return;
}
}
}
}
}
}using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class Move : MonoBehaviour
{
public float _speed = 2f;
// Start is called before the first frame update
void Start()
{
}
// Update is called once per frame
void Update()
{
Vector3 pos = Vector3.zero;
if (Input.GetKey(KeyCode.A))
{
pos.x -= Time.deltaTime * _speed;
}
else if (Input.GetKey(KeyCode.D))
{
pos.x += Time.deltaTime * _speed;
}
else if (Input.GetKey(KeyCode.W))
{
pos.z += Time.deltaTime * _speed;
}
else if (Input.GetKey(KeyCode.S))
{
pos.z -= Time.deltaTime * _speed;
}
CheckHit(pos);
}
private void CheckHit(Vector3 pos)
{
this.transform.position += pos;
if (SDFCreator.SDFCollider == null)
{
return;
}
for (int i = 0; i < SDFCreator.SDFCollider.Length; i++)
{
Vector3 radius = (SDFCreator.SDFCollider[i].transform.position - this.transform.position).normalized * 0.4f;
Vector3 newPos = this.transform.position;
Vector3 circle = newPos + radius;
Vector3Int vector = new Vector3Int(Mathf.RoundToInt(circle.x * SDFCreator.floatToIntNum), Mathf.RoundToInt(circle.y * SDFCreator.floatToIntNum), Mathf.RoundToInt(circle.z * SDFCreator.floatToIntNum));
if (SDFCreator.mSDFValue.ContainsKey(vector))
{
//Debug.Log("distance:" + SDFCreator.mSDFValue[vector]);
if (SDFCreator.mSDFValue[vector] < 0)
{
//Debug.LogError("hit");
this.transform.position -= pos;
break;
//Vector3 normalDir =
}
}
}
}
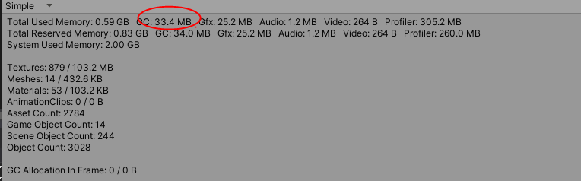
}cpu consumption comparison:
Signed distance field:

Collision detection consumption

Memory:
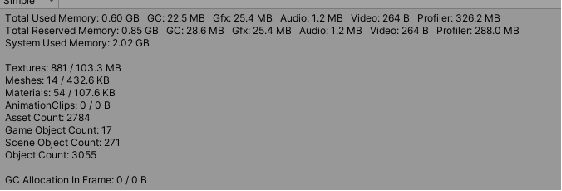
Signed distance field consumption:
Collision detection consumption:
Soft shadows:

This is demonstrated by creating floors and squares with a light step.
reference resources: https://www.shadertoy.com/view/lsKcDD
The steps are:
1. From the perspective of camera (after rotation and position offset), step in the straight line direction for each pixel. If the object with a signed distance field can be found in the step direction, proceed to the next step. Here, he found two real-time distance fields. One is the floor. The distance field of the floor is easy to determine, which is a height. If it is at this height, it is the floor. The other is the box box , the way to judge box is to abs(p) let him change from six quadrants to three positive quadrants first, because box is symmetrical. Then subtract his length, width and height
float3 d = abs(p) - b; If D is negative, it means that this point is in the box, then min(max(d.x, max(d.y, d.z)), 0.0)=0, and length(max(d, 0.0)) is also 0 If one is not negative, there is a distance.
2. If there is a colliding object, find its normal directly from the radius to the distance t (this is also the advantage of the signed distance field. Unlike ordinary light stepping, it has a fixed step every time. It accurately guides where the next colliding point is, so the radius can be easily determined).
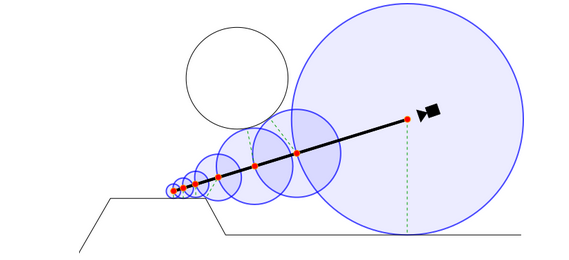
The normal is obtained by constructing four points - k0 = {1, - 1, - 1}, k1 = {- 1, - 1,1}, k2 = {- 1,1,-1} and k3 = {1,1,1} In fact, you build a cone, the current P point is in the center of the cone, and then offset the four points. Finally, we can find the slope of the current P.
vec3 calcNormal( in vec3 pos )
{
vec2 e = vec2(1.0,-1.0)*0.5773*0.0005;
return normalize( e.xyy*map( pos + e.xyy ).x +
e.yyx*map( pos + e.yyx ).x +
e.yxy*map( pos + e.yxy ).x +
e.xxx*map( pos + e.xxx ).x );
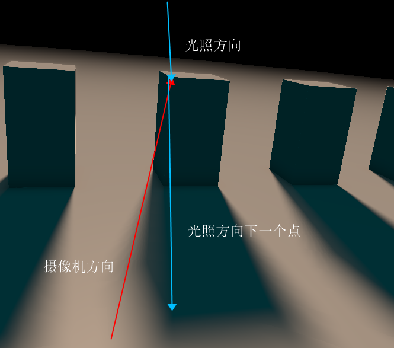
}3. Then the key is to calculate the shadow:
Shadow calculation is to find the point where the current camera steps in, and then study the lighting direction to find the next point, which is our shadow point.
4. Finally, if he wants to present soft shadows, he must have some virtualization effects. Here, the formula of s*s*(3.0-2.0*s) is used. His meaning is the attenuation of the third power. The principle of using this formula is to get the values of f(0)=0,f(1)=1,f(0.5)=0.5.
5. Then another step is to calculate Ao, where Ao is to find the nearest object along the normal direction. For example, if the ground is close to the object, the next point in the normal direction is the point of the ground. Naturally, we can get d, and we can calculate his Ao for so long. Determine the depth of a Ao color based on their distance.
Others are more common:
Full code:
//
// Testing Sebastian Aaltonen's soft shadow improvement
//
// The technique is based on estimating a better closest point in ray
// at each step by triangulating from the previous march step.
//
// More info about the technique at slide 39 of this presentation:
// https://www.dropbox.com/s/s9tzmyj0wqkymmz/Claybook_Simulation_Raytracing_GDC18.pptx?dl=0
//
// Traditional technique: http://iquilezles.org/www/articles/rmshadows/rmshadows.htm
//
// Go to lines 54 to compare both.
// make this 1 is your machine is too slow
#define AA 1
float3 _Light;
//------------------------------------------------------------------
float sdPlane(float3 p)
{
return p.y;
}
float sdBox(float3 p, float3 b)
{
float3 d = abs(p) - b;//abs(p) converts 6 quadrants into 3 imaginations (all positive numbers), and subtracts b to subtract its length, width and height
//If d is negative, it means that this point is in the box, then min(max(d.x, max(d.y, d.z)), 0.0)=0, and length(max(d, 0.0)) is also 0
//If there is a non negative number, there is a distance
return min(max(d.x, max(d.y, d.z)), 0.0) + length(max(d, 0.0));
}
//------------------------------------------------------------------
//Determine whether the stepping position is the floor or the box through the distance field
float map(in float3 pos)
{
float3 qos = float3(frac(pos.x + 0.5) - 0.5, pos.yz);//Here, multiple can be divided according to the x-axis by frac remainder
return min(sdPlane(pos.xyz - float3(0.0, 0.00, 0.0)),
sdBox(qos.xyz - float3(0.0, 0.25, 0.0), float3(0.2, 0.5, 0.2)));
}
//------------------------------------------------------------------
//ro is the current point and rd is the light direction
float calcSoftshadow(in float3 ro, in float3 rd, in float mint, in float tmax, int tech)
{
float res = 1.0;
float t = mint;
float ph = 1e10; // big, such that y = 0 on the first iteration
for (int i = 0; i < 32; i++)
{
float h = map(ro + rd * t);
// traditional tech
if (tech == 0)
{
//The traditional method is to divide the distance of the last position by the distance of the 10 * position
res = min(res, 10.0*h / t);
}
// improved tech
else
{
// use this if you are getting artifact on the first iteration, or unroll the
// first iteration out of the loop
//float y = (i==0) ? 0.0 : h*h/(2.0*ph);
float y = h * h / (2.0*ph);
float d = sqrt(h*h - y * y);
res = min(res, 10.0*d / max(0.0, t - y));
ph = h;
}
t += h;//Only when the road is h so far away can we find the projection position in rd direction of the current position from the light direction
if (res<0.0001 || t>tmax) break;
}
res = clamp(res, 0.0, 1.0);
return res * res*(3.0 - 2.0*res);//The output here is the attenuation to the third power. The principle of using this formula is to get the values of f(0)=0,f(1)=1,f(0.5)=0.5
}
//Find the points by stepping up, down, left and right distance fields, and then add them and have weights to get the normal information of his center
float3 calcNormal(in float3 pos)
{
//We construct four points k0 = {1,-1,-1}, k1 = {-1,-1,1}, k2 = {-1,1,-1} and k3 = {1,1,1} In fact, you build a cone, the current P point is in the center of the cone, and then offset the four points. Finally, we can find the slope of the current P.
float2 e = float2(1.0, -1.0)*0.5773*0.0005;
return normalize(e.xyy*map(pos + e.xyy) +
e.yyx*map(pos + e.yyx) +
e.yxy*map(pos + e.yxy) +
e.xxx*map(pos + e.xxx));
}
//ro is the camera position and rd is the step direction
float castRay(in float3 ro, in float3 rd)
{
float tmin = 1.0;
float tmax = 20.0;
#if 1
// bounding volume
float tp1 = (0.0 - ro.y) / rd.y; if (tp1 > 0.0) tmax = min(tmax, tp1);
float tp2 = (1.0 - ro.y) / rd.y; if (tp2 > 0.0) {
if (ro.y > 1.0) tmin = max(tmin, tp2);
else tmax = min(tmax, tp2);
}
#endif
//Here, first take the radius of 0.0005 as the starting point to step, and find the minimum distance between each rd direction and plane and box as the size of the next step. Keep stepping out of range
float t = tmin;
for (int i = 0; i < 64; i++)
{
float precis = 0.0005*t;
float res = map(ro + rd * t);
if (res<precis || t>tmax) break;//Res < precis indicates that the current point is inside the object and stops stepping
t += res;
}
if (t > tmax) t = -1.0;
return t;
}
float calcAO(in float3 pos, in float3 nor)
{
float occ = 0.0;
float sca = 1.0;
for (int i = 0; i < 5; i++)
{
float h = 0.001 + 0.15*float(i) / 4.0;
float d = map(pos + h * nor);//Find the nearest object in the normal direction. For example, if the ground is close to the object, the next point in the normal direction is the point of the ground. Naturally, we can get d, and we can calculate his ao for so long.
occ += (h - d)*sca;//Determine the depth of an ao color based on their distance
sca *= 0.95;//Depth decrement
}
return clamp(1.0 - 1.5*occ, 0.0, 1.0);
}
//ro is the camera position and rd is the step direction
float3 render(in float3 ro, in float3 rd, in int tech)
{
float3 col = float3(0,0,0);
float t = castRay(ro, rd);//With the distance fields sdplane and sdbox, you can step to a specified point in a large range to get the distance t in this direction
if (t > -0.5)
{
float3 pos = ro + t * rd;//Camera direction stepping
float3 nor = calcNormal(pos);
// material
float3 mate = float3(0.3,0.3,0.3);
// key light
//float3 lig = normalize(float3(-0.1, 0.3, 0.6));
float3 hal = normalize(_Light - rd);
//Diffuse reflection and its shadow. The shadow is obtained by stepping. The next projected point in the light direction is the shadow point, and then it becomes a soft shadow with the attenuation of the third power
float dif = clamp(dot(nor, _Light), 0.0, 1.0) *
calcSoftshadow(pos, _Light, 0.01, 3.0, tech);//Step in the direction of the camera and look at the shadow in the direction of illumination
//Highlight
float spe = pow(clamp(dot(nor, hal), 0.0, 1.0), 16.0)*
dif *
(0.04 + 0.96*pow(clamp(1.0 + dot(hal, rd), 0.0, 1.0), 5.0));
//The color is the material itself, and the color is combined with diffuse reflection and soft shadow
col = mate * 4.0*dif*float3(1.00, 0.70, 0.5);
//Plus highlights
col += 12.0*spe*float3(1.00, 0.70, 0.5);
// ambient light
float occ = calcAO(pos, nor);
float amb = clamp(0.5 + 0.5*nor.y, 0.0, 1.0);
col += mate * amb*occ*float3(0.0, 0.08, 0.1);
// fog
col *= exp(-0.0005*t*t*t);
}
return col;
}
float3x3 setCamera(in float3 ro, in float3 ta, float cr)
{
float3 cw = normalize(ta - ro);//A point outside the camera and the direction obtained by the camera, this is one of the axes
float3 cp = float3(sin(cr), cos(cr), 0.0);//Camera rotation angle
float3 cu = normalize(cross(cw, cp));//Cross multiply to get an axis of the camera
float3 cv = normalize(cross(cu, cw));//Another axis is obtained by another cross multiplication.
return float3x3(cu, cv, cw);//Camera coordinates (xyz axis)
}
void mainImage(out float4 fragColor, in float2 fragCoord, in float2 iResolution)
{
// camera
float iTime = _Time.y;
float an = 12.0 - sin(0.1*iTime);
float3 ro = float3(3.0*cos(0.1*an), 1, -3.0*sin(0.1*an));//Camera position
float3 ta = float3(0.0, 2, 0.0);//The point outside determines the coordinate system of the camera
// camera-to-world transformation
float3x3 ca = setCamera(ro, ta, 0.0);
int tech = (frac(iTime / 2.0) > 0.5) ? 1 : 0;
float3 tot = float3(0,0,0);
#if AA>1
for (int m = 0; m < AA; m++)
for (int n = 0; n < AA; n++)
{
// pixel coordinates
float2 o = float2(float(m), float(n)) / float(AA) - 0.5;
float2 p = (-iResolution.xy + 2.0*(fragCoord + o)) / iResolution.y;
#else
float2 p = (-iResolution.xy + 2.0*fragCoord) / iResolution.y;//(- iResolution.xy + 2.0*fragCoord) is to set the camera to - 1 to 1, and then divide iresolution Y is equivalent to multiplying by one screen size
#endif
// ray direction
float3 rd = mul(ca, normalize(float3(p.xy, 2.0)));//Screen space coordinates go to camera space
// render
float3 col = render(ro, rd, tech);
// gamma
col = pow(col, 0.4545);//pow(col, float3(0.4545));
tot += col;
#if AA>1
}
tot /= float(AA*AA);
#endif
fragColor = float4(tot, 1.0);
}Environmental masking (AO)
What is environmental masking (AO)

The effect on the left is not Ao. You can see that its stereoscopic sense is relatively poor. Some positions that should be difficult to be illuminated are bright. After wearing Ao on the right, his indirect light effect is more three-dimensional. Ao is also a very important module in global illumination. There are many Ao methods on the market, such as mapping Ao, ssao, hbao, gtao, dfao, etc.
dfao is the ao effect based on signed distance field integrated in UE.
The advantages of dfao are:
Dfao produces a more accurate ao effect than the general real-time screen space ao through the distance field,
It can provide the shielding effect of ambient light specular reflection, improve the real-time effect of the picture without too much consumption.
Disadvantages:
Dfao is not suitable for too fine object projection, because the construction of dfao is mostly a fitting of the object;
The masking effect sometimes affects the luster of the covering; Not suitable for hosts other than pc; Will interact with other transparency effects
Conflicts, etc.

His construction method:
UE uses violence to build a field, that is, directly iterate 32 * 32 * 32 points, then emit a lot of light around each point, and then save the minimum distance to be handed over as the value of the distance field at this point.
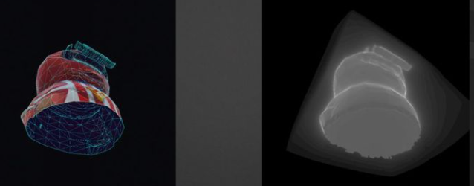

In terms of search, a kd tree can be used to speed up the search:
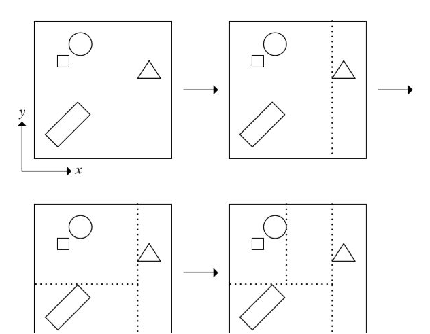
In three-dimensional space, it is a tree structure that divides all objects according to xyz three axes. Its advantage is that it can quickly find nearby objects. Its search method is to first find the object in the bifurcation near the tree species, and then search whether the object within this radius is closer with the object to be found and the position of the object as the radius. This is because the nearest object may not be on one side of its own tree, but on the other side. So we need to find this radius again.
The above is some knowledge about the signed distance field that I have learned and practiced. If you have any questions, please point out.