Reference material:
A note of someone's quantification principles
https://blog.csdn.net/sinat_31425585/article/details/101607785
Someone's more detailed introduction to int8
https://zhuanlan.zhihu.com/p/58182172
Someone's understanding of ncnn quantification principles and source codes (ncnn quantization is based on tensorRT improvements)
https://zhuanlan.zhihu.com/p/72375164
 

1. Rough Understanding of Two Diagrams and Quantitative Ideas

A sentence maps the original value equal scale to -127~127 for int8.
The original idea was to use the maximum absolute value of the original value as the threshold value, but if the original value is not evenly distributed, some of the value domains are wasted, resulting in a great loss of precision. (For example, the original range of values is -1270.0~+1270.0, but most of them are 0~+10, so quantification becomes int8+1 all).
So in many cases, it is intercepting a portion of it (that is, using a small threshold) to establish a mapping relationship. Why (why is the saturated intercept on the right ok ay? https://zhuanlan.zhihu.com/p/58182172)

The whole question of quantification becomes how to find the optimal threshold to minimize the loss of precision?
 

2. Model reasoning after int8 quantification

First, take multiplication in a simple network layer as an example to see the forward inference formula quantified with int8:

Zoom factor: s = 127 / T, this T Is the threshold value to be found on the original value.
Input Vector:
    input_int8 = s_input * input_fp,
input_int8 yes input Quantified value, s_input yes input Zoom factor of, input_fp yes input Original value, fp Express float type
 Model weight:
    weight_int8 = s_weght * weight_fp,
weight_int8 yes weght Quantified value, s_weight yes weight Zoom factor of, weight_fp yes weight Original value
forward Calculates the product of the two: 
    input_fp * weight_fp = (input_int8 * weight_int8) / (s_input * s_weight)
order ss_fp = 1 / (s_input * s_weight), So this calculation can be done in two steps:
First is int8 Calculation:
    inner_int8 = (input_int8 * weight_int8)
The second is multiplication float Coefficient of type reverts back to original float type
    output_fp = inner_int8 * ss_fp

Summary: In each layer of calculation, you need to quantify feature map to INT8, then weights to INT8, and finally convolution to get the output value of INT32, the output value multiplied by scale (float) value to reverse quantify to float, and then add bias in floating-point format as the next input. (This passage is https://zhuanlan.zhihu.com/p/58182172 Inside, it's about the bottom quantization of ncnn).
 

3. How to find the optimal threshold T?

With the threshold T and the zoom factor, the problem is almost solved.
How do I find the optimal threshold T? By calculating the difference between the two data distributions before and after quantification, the threshold T with the smallest difference in distribution is the optimal threshold.
The KL divergence (relative entropy) is used to calculate the difference between two distributions:

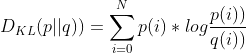
p(i) denotes the value of an element in the original distribution P, and q(i) denotes the value of an element in the quantified distribution Q.
However, the values are continuous in the process of model inference. How can P and Q distributions be obtained? It is represented by histogram statistics.

Histogram statistics (that is, distribution P) of the original values are calculated:
 

1. Calculate Original fp Maximum absolute value of type data(That is, the maximum of the absolute value of the maximum and minimum): 
    mav = max(abs(min_v), abs(max_v))
2. Divide raw data into 2048 bins, each bin Width:
    interval = mav / 2048
3. Histogram of Statistical Original Values, p(i)Is the first i individual bin Number of original data points in.

Next comes the process of finding the optimal threshold T, which is the center of the entire quantization algorithm (remember that T is <=mav and uses -T and + T to truncate data):

for num_bins from 127 to 2048:
    a. T_cur = interval * num_bins, (ncnn Is used(interval+0.5)*num_bins, Take a bin Center Point),
       Use T_cur Stage data, Get Truncated Distribution P'(Values outside the truncation zone are added to the last value of the truncation zone, such as num_bins Is 200, That's the last one bin The serial number of the is 200,  Then 201~2048bin Frequency on(Frequency or frequency?)Were added to the 20th bin upper)
    b. hold P'Distribution maps to Q, Q Of bins Is 128, Q Is the quantified data distribution
       (Be careful, Here is the direct-to-histogram P'Map to 128 bins Histogram Q, Instead of mapping the original data to int8 Restatistics Histogram)
       (see https://zhuanlan.zhihu.com/p/7237516 The general idea to know ncnn is to put the original num_ The histogram of bins is redistributed evenly into 128 bins)
    c. take Q Extend to and P'Same length, obtain Q_expand(To calculate KL Spread assumes two distributions have the same length)
    d. Calculation P'and Q_expand Of KL divergence, And judge KL Is divergence minimum

The process can be seen https://zhuanlan.zhihu.com/p/72375164 The understanding of NCNN quantification source code is very detailed and worth looking at. It can be understood more deeply.

Step c above extends Q to the same length as P', as illustrated below (from https://zhuanlan.zhihu.com/p/72375164 Copied from:

P=[1 2 2 3 5 3 1 7]     // Statistical Histogram of fp32, T=8
// Assume that only two bins are quantified, that is, only -1/0/+1 is the quantified value
Q=[1+2+2+3, 5+3+1+7] = [8, 16]
// P and Q cannot do KL divergence now, so extend Q to the same length as P
Q_expand = [8/4, 8/4, 8/4, 8/4, 16/4, 16/4, 16/4, 16/4] = [2 2 2 2 4 4 4 4]
D = KL(P||Q_expand)  // This allows calculation of KL dispersion

This extended operation, like up-sampling of an image, uploads the low-precision statistical histogram (Q) to the high-precision statistical histogram (Q_expand) of the up-sampling. Q_Sampled on Q since one bin in Q corresponds to four bins in P During expansion, all data is divided by 4.

done.