1, Problem description

In the actual daily life, people often encounter the following problems: find the function in a given definition field X f ( x ) f(x) The optimal value corresponding to f(x). Here, the minimum value problem is taken as an example (the maximum value problem can be equivalent to the minimum value problem), which is formalized as: min ⁡ x ∈ C f ( x ) \min _{x \in C }f(x) minx∈C​f(x)

If X is a discrete finite value, the optimal solution of the problem can be obtained by the finite value method; If X is continuous, but f ( x ) f(x) If f(x) is convex, the optimal solution can be obtained by gradient descent and other methods; If X is continuous and f ( x ) f(x) f(x) is non convex. Although the solution of the problem can be found according to the existing approximate solution method, whether the solution is optimal remains to be considered. In many cases, if the initial value is not selected well, it is very easy to fall into the local optimal value.

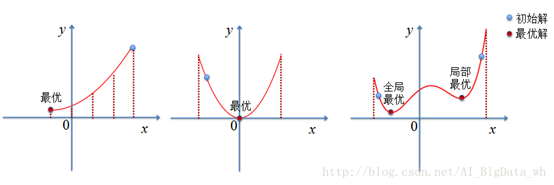
Therefore, in order to jump to the optimal solution more effectively, simulated annealing came into being

• However, how does simulated annealing algorithm simulate the principle of metal annealing?
  1. Mainly apply the theory of thermodynamics to statistics, and imagine every point in the search space as a molecule in the air;
  2. The energy of a molecule is its own kinetic energy;
  3. Every point in the search space also has "energy" like air molecules to indicate the suitability of the point to the proposition.
  4. The algorithm starts with an arbitrary point in the search space: each step first selects a "neighbor", and then calculates the probability of reaching the "neighbor" from the existing location.
  5. If the probability is greater than the given threshold, jump to "neighbor"; If the probability is small, stay in the original position.
  6. As the temperature decreases, the jump becomes more and more random, and the optimal solution becomes more and more stable
  (gif takes 10s, quoted from wiki)

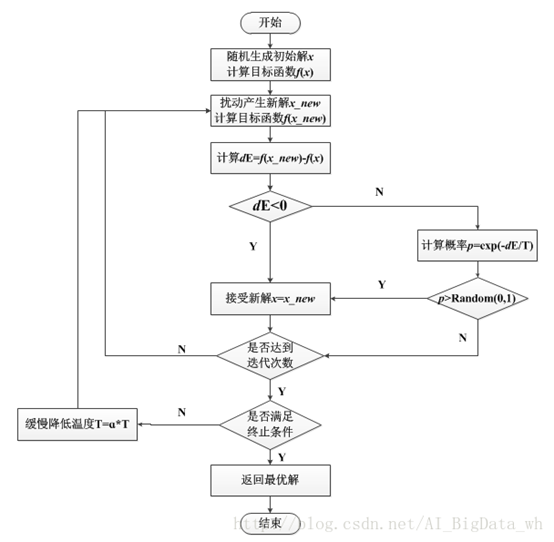
2, Algorithm implementation

According to the principle of thermodynamics, when the temperature is T, the energy difference is d E dE The probability of dE cooling is p ( d E ) p(dE) p(dE), expressed as p ( d E ) = e x p ( d E k T ) p(dE)=exp(\frac{dE}{kT}) p(dE)=exp(kTdE​)

Quantized extracted exp and independent variables

In a simulated annealing, the temperature tt needs to cover three times of the data range. I think it is because it conforms to the normal distribution 3 δ 3δ three δ Most of the coverage (probably) 96 96% 96) data range

Because it is a randomized algorithm, the whole timing function, if there is time, run more, and the optimal solution is still very easy to do

3, Examples

1. Two dimensional Fermat point

There are n points on the two-dimensional plane, and the coordinates of the ith point are (xi,yi). Please find a point to minimize the sum of the distances from the point to the n points. The point can be selected at any position in the plane or even coincide with the positions of the n points.

#include<iostream>
#include<cmath>
#include<ctime>
#include<cstring>
#include<algorithm>

#define x first
#define y second
using namespace std;

typedef pair<double ,double >pdd;
double ans;
int n;
pdd q[109];

inline int read ()
{
    int x; bool flag = 1; char ch = getchar();
    while(ch>'9'&&ch<'0')if(ch=='-')flag = 0,ch= getchar();
    while(ch<='9'&&ch>='0')x=(x<<1)+(x<<3)+ch-'0',ch = getchar ();
    if(!flag)return ~(x-1);
    else return x;
}

inline double  randx (double l , double r)
{
    return (double)rand() / RAND_MAX * (r - l ) + l;
}

inline double dis(pdd a, pdd b)
{
    return sqrt((a.x - b.x)*(a.x - b.x ) + (a.y - b.y ) * (a.y - b.y ));
}

double clac (pdd k)
{
    double res=0;
    for(int i= 1;i<=n;i ++)res+=dis(k,q[i]);
    ans =min(ans,res);
    return res;
}
void simulate_anneal()
{
    pdd dx (randx(0,10000),randx (0,10000));
    for(double  t = 1e4; t >1e-4 ; t*=0.99)
    {
        pdd dt  (randx (dx.x -t,dx.x + t) , randx (dx.y-t,dx.y+t));
        double dlata= clac(dt)- clac(dx);
        if (exp(-dlata/t) > randx(0, 1) ) dx =dt ;
    }
}

signed main(void)
{
    ans = 1e8+9;
    n=read();
    for(int i = 1 ; i <=n; i ++ )cin>>q[i].x>>q[i].y;
    for(int i= 1; i<=100;i++)simulate_anneal();
    printf ("%.0lf",ans);
}