Six basic sorting
Learning records
I Simple sort
1.1 bubble sorting
It means that two adjacent elements are compared, and the largest element is selected at each time and placed on the last side
package sort;
/**
* Bubble sorting
* It means that two adjacent elements are compared, and the largest element is selected at each time and placed on the last side
*/
public class Bubble {
/**
* Sort the elements in array a
*
* @param a
*/
public static void sort(Comparable[] a) {
for (int i = 1; i < a.length; i++) {
for (int j = 0; j < a.length - i; j++) {
if (greater(a[j],a[j+1])) {
exch(a,j,j+1);
}
}
}
}
/**
* Compare whether the v element is larger than the w element
*
* @param v
* @param w
* @return
*/
public static boolean greater(Comparable v, Comparable w) {
return v.compareTo(w) > 0;
}
/**
* Data element i,j exchange location
*
* @param a
* @param i
* @param j
*/
public static void exch(Comparable[] a, int i, int j) {
Comparable temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
Time complexity analysis:
Worst case scenario:
Element comparison times: N^2/2-N/2
Number of element exchange: N^2/2-N/2
Total execution times: N^2-N;
According to the large o rule, the highest order term is retained, and the final time complexity is O(N^2)
1.2 select sort
In each traversal, it is assumed that the first element is the minimum value, and the values at other indexes are compared in turn. If the value at the current index is greater than the value at some other index, it is assumed that the value at some other index is the minimum value. Finally, the index where the minimum value is located can be found, and then the values at the first index and the minimum value index can be exchanged
package sort;
//Select sort
public class Selection {
/**
* Sort the elements in array a
*
* @param a
*/
public static void sort(Comparable[] a) {
for (int i = 0; i < a.length-1; i++) {
//Record minimum index
int minIndex=i;
for (int j = i+1; j < a.length; j++) {
//Find minimum index
if (greater(a[minIndex],a[j])) {
minIndex = j;
}
}
//Exchange the index minIndex where the minimum value is located and the value at index i
exch(a,minIndex,i);
}
}
/**
* Compare whether the v element is larger than the w element
*
* @param v
* @param w
* @return
*/
public static boolean greater(Comparable v, Comparable w) {
return v.compareTo(w) > 0;
}
/**
* Data element i,j exchange location
*
* @param a
* @param i
* @param j
*/
public static void exch(Comparable[] a, int i, int j) {
Comparable temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
Time complexity analysis:
Worst case scenario:
Element comparison times: N^2/2-N/2
Number of element exchange: N-1
The total number of executions is: N^2+N/2-1;
According to the large o rule, the highest order term is retained, and the final time complexity is O(N^2)
1.3 insert sort
All elements are divided into two groups, sorted and unordered
Inserts the first element in an unordered group into a sorted group
When inserting, traverse the sorted array in reverse order, compare with the elements to be inserted in turn, and exchange the element position if it meets the conditions until an element less than or equal to the element to be inserted is found, that is, find the final position of the element in the sorted group
package sort;
//Insert sort
public class Insertion {
/**
* Sort the elements in array a
*
* @param a
*/
public static void sort(Comparable[] a) {
//By default, the first element is a sorted group, and the subsequent elements are unordered
for (int i = 1; i < a.length; i++) {
for (int j = i; j > 0; j--) {
//Compare the values at index j and index j-1. If the value at j-1 is greater than the value at j, exchange the elements. Otherwise, find the appropriate position and exit the loop
if (greater(a[j-1],a[j])) {
exch(a,j-1,j);
}else {
break;
}
}
}
}
/**
* Compare whether the v element is larger than the w element
*
* @param v
* @param w
* @return
*/
public static boolean greater(Comparable v, Comparable w) {
return v.compareTo(w) > 0;
}
/**
* Data element i,j exchange location
*
* @param a
* @param i
* @param j
*/
public static void exch(Comparable[] a, int i, int j) {
Comparable temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
Time complexity analysis:
Worst case scenario:
Element comparison times: N^2/2-N/2
Number of element exchange: N^2/2-N/2
Total execution times: N^2-N;
According to the large o rule, the highest order term is retained, and the final time complexity is O(N^2)
II Advanced sorting
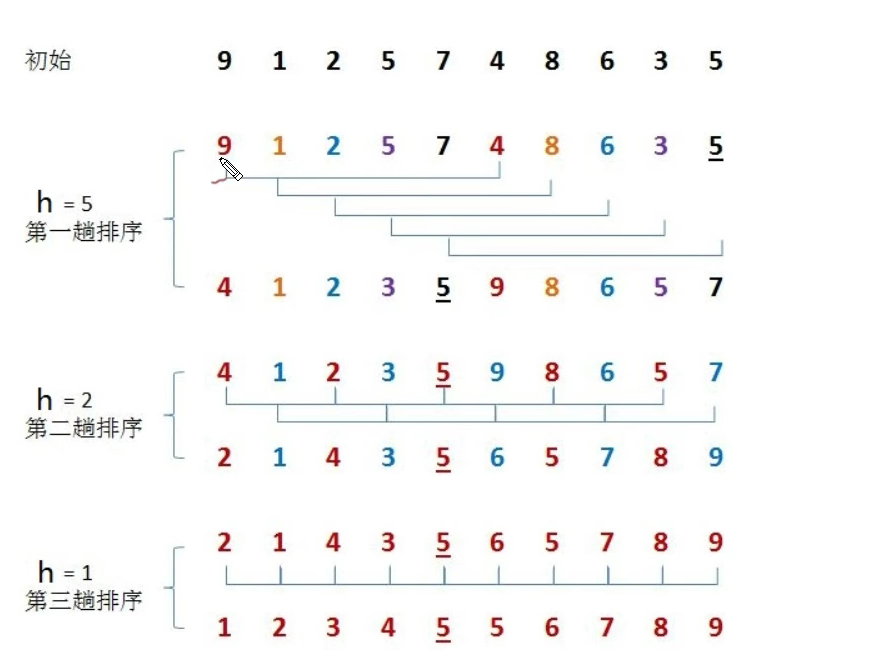
2.1 Hill sorting
Hill sort is a kind of insert sort, also known as "narrow incremental sort", which is a more efficient and improved version of insert sort
Select a growth amount h and group the array according to the growth amount h as the basis for data grouping;
Insert and sort each group of data with the best group;
Reduce the growth to 1 and repeat the second step
package sort;
public class Shell {
/**
* Sort the elements in array a
*
* @param a
*/
public static void sort(Comparable[] a) {
//1. Determine the growth amount h according to the array length
int h = a.length >> 1;
//2. Hill sort
while (h >= 1) {
//sort
//Find element to insert
for (int i = h; i < a.length; i++) {
//Insert the element to be inserted into the ordered sequence
for (int j = i; j >=h; j-=h) {
//The element to be inserted is a[j]
if (greater(a[j-h],a[j])) {
exch(a,j,j-h);
}else {//The element to be inserted finds the appropriate position and ends the loop
break;
}
}
}
//Decrease the value of h
h = h >> 1;
}
}
/**
* Compare whether the v element is larger than the w element
*
* @param v
* @param w
* @return
*/
public static boolean greater(Comparable v, Comparable w) {
return v.compareTo(w) > 0;
}
/**
* Data element i,j exchange location
*
* @param a
* @param i
* @param j
*/
public static void exch(Comparable[] a, int i, int j) {
Comparable temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
Time complexity analysis:
Ex ante analysis is complicated. If mathematics is not very good, we won't analyze it
Post analysis:
package sort;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Objects;
public class ShellCompareToInsertion {
public static void main(String[] args) throws IOException {
//Create an Arraylist collection and save the read integers
ArrayList<Integer> list = new ArrayList<>();
//Create a cache read stream BufferedReader, read the data, and store it in the Arraylist
BufferedReader reader = new BufferedReader(new InputStreamReader(Objects.requireNonNull(ShellCompareToInsertion.class.getClassLoader().getResourceAsStream("Test file"))));
String line = null;
while ((line = reader.readLine()) != null) {
int i = Integer.parseInt(line);
list.add(i);
}
//Convert the ArrayList collection to an array
Integer[] a = new Integer[list.size()];
list.toArray(a);
Integer[] b = a.clone();
//Call test code
testInsertion(a);
testshell(b);
}
//Test Hill sort
public static void testshell(Integer[] a) {
//Get start time
long start = System.currentTimeMillis();
//Execution algorithm
Shell.sort(a);
//Get end time
long end = System.currentTimeMillis();
//Calculate the program execution time and output
System.out.println("Hill sort execution time:" +(start-end)+"millisecond");
}
//Test insert sort
public static void testInsertion(Integer[] a) {
//Get start time
long start = System.currentTimeMillis();
//Execution algorithm
Insertion.sort(a);
//Get end time
long end = System.currentTimeMillis();
//Calculate the program execution time and output
System.out.println("Insert sort execution time:" +(start-end)+"millisecond");
}
}
2.2 merge sort
2.2.1 recursion
When a method is defined, the method itself is called inside the method
A large complex problem is transformed into a smaller problem similar to the original problem
Note: the boundary must be set to end the recursion, because each recursive call will open up a new space in the stack memory and re execute the method. If the recursion level is too deep, it is easy to cause stack memory overflow
Example: find the factorial of N
package sort;
public class TestFactorial {
public static void main(String[] args) {
//Factoring N
long result = factorial(5);
System.out.println("result = " + result);
}
//Find the factorial of n
private static long factorial(int i) {
if (i==1) {
return 1;
}
return i*factorial(i-1);
}
}
2.2.2 merge sort
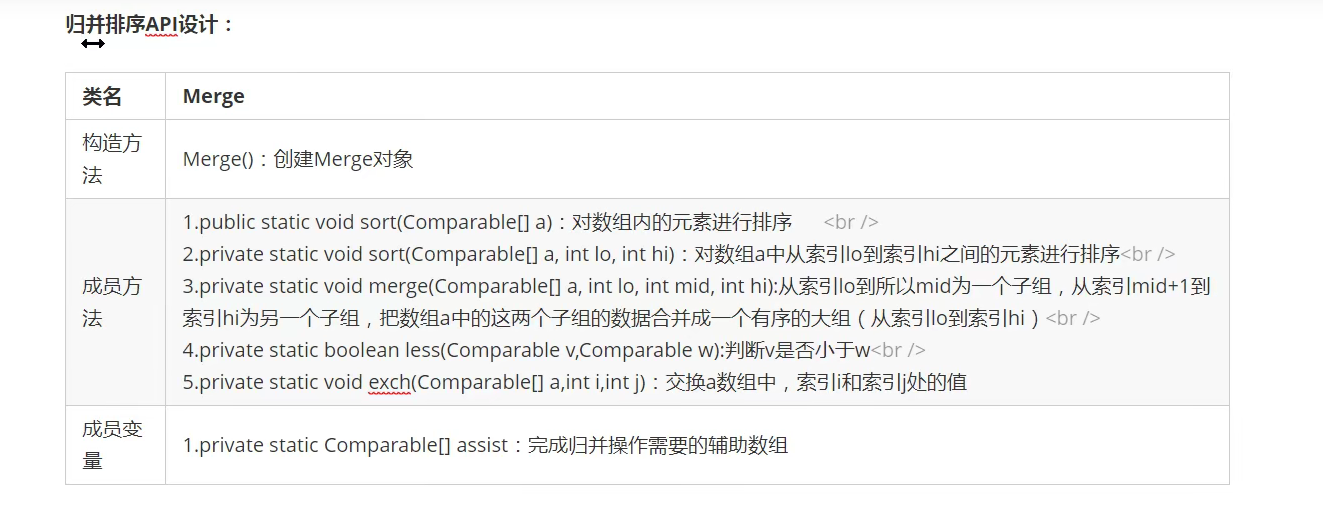
Merge sort is an effective sort algorithm based on merge operation. It is a very typical application of divide and conquer method The ordered subsequences are combined to obtain a completely ordered sequence
That is, first order each subsequence, and then order the subsequence segments,
Split a group of data into two subgroups with equal elements as far as possible, and continue to split each word group until the number of elements in each subgroup is 1
Merge two adjacent subgroups into an ordered large group,
Repeat the previous step until there is only one group

package sort;
/**
* Merge sort
*/
public class Merge {
//Auxiliary array needed for merge sort
private static Comparable[] assist;
/**
* Sort the elements in array a
*
* @param a
*/
public static void sort(Comparable[] a) {
//Initialize auxiliary array assist
assist = new Comparable[a.length];
//Define a lo variable and hi variable to record the smallest index and the largest index in the array respectively
int lo = 0;
int hi = a.length - 1;
//Call the sort overloaded method to sort the elements in array a from index lo to hi
sort(a, lo, hi);
}
/**
* Sort the elements from lo to hi in array a
*
* @param a
* @param lo
* @param hi
*/
public static void sort(Comparable[] a, int lo, int hi) {
//Do safety verification
if (hi <= lo) {
return;
}
int mid = lo + (hi - lo)/2;
//Sort each group of data separately
sort(a, lo, mid);
sort(a, mid + 1, hi);
//Then merge the data in the two groups
merge(a, lo, mid, hi);
}
/**
* In the array, from lo to mid is a group, and from mid+1 to hi is a group. Merge the two groups of data
*
* @param a
* @param lo
* @param mid
* @param hi
*/
public static void merge(Comparable[] a, int lo, int mid, int hi) {
//Define three pointers
int i = lo;
int p1 = lo;
int p2 = mid + 1;
//Traverse, move the p1 and p2 pointers, compare the value at the corresponding index, find the smallest one, and put it at the corresponding index of the auxiliary array
while (p1 <= mid && p2 <= hi) {
//Compare the values at the corresponding index
if(less(a[p1],a[p2])) {
assist[i++] = a[p1++];
}else {
assist[i++] = a[p2++];
}
}
//Traversal. If the p1 pointer is not completed, move the p1 pointer in sequence and put the corresponding element at the corresponding index of the auxiliary array
while (p1<=mid) {
assist[i++] = a[p1++];
}
//Traversal. If the p2 pointer is not completed, move the p2 pointer in sequence and put the corresponding element at the corresponding index of the auxiliary array
while (p2<=hi) {
assist[i++] = a[p2++];
}
//Copy the elements in the auxiliary array to the original array
for (int index = lo;index<=hi;index++) {
a[index] = assist[index];
}
}
/**
* Compare whether the v element is smaller than the w element
*
* @param v
* @param w
* @return
*/
public static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
/**
* Data element i,j exchange location
*
* @param a
* @param i
* @param j
*/
public static void exch(Comparable[] a, int i, int j) {
Comparable temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
Time complexity analysis:
Worst case scenario:
Element comparison times: the comparison times of the nth layer is 2^n
Merge sort is used to split log(2)n, so there are log2(n) layers
Total execution times: log(2)n * 2^log(2)n = log(2) * n
According to the large o rule, the highest order term is retained, and the final time complexity is O (nlogn)
Disadvantages: typical space for time operation
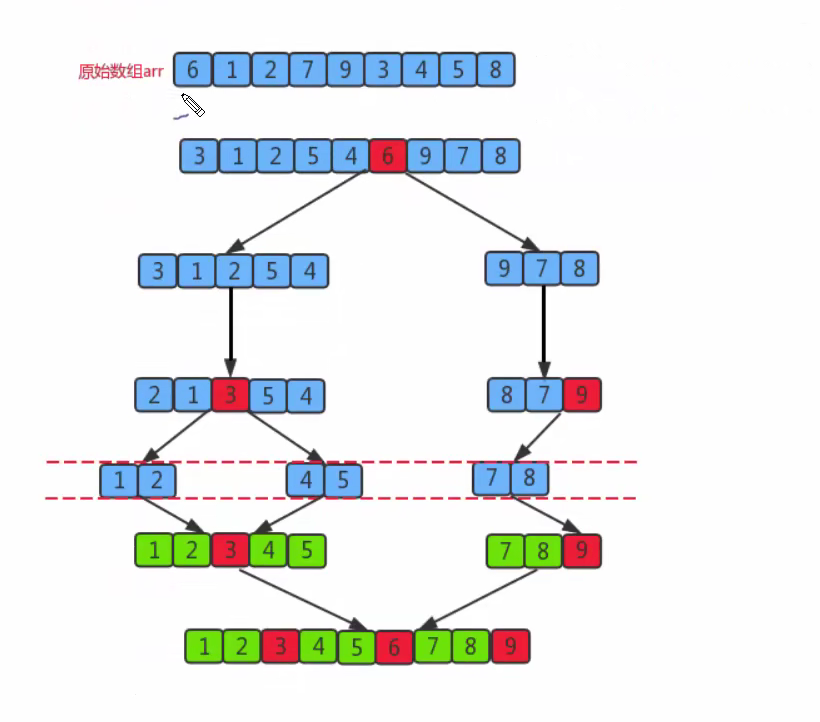
2.3 quick sort
Firstly, a boundary value is defined, and the array is divided into left and right parts through the boundary value;
Send the data greater than or equal to the boundary value to the right of the array, and the data less than the boundary value to the left of the array. At this time, all elements in the left part are less than or equal to the boundary value, while all elements in the right part are greater than or equal to the boundary value;
Then, the data on the left and right can be sorted independently. For the array data on the left, a boundary value can be taken and the part can be divided into left and right parts. Similarly, the smaller value is placed on the left and the larger value is placed on the right. The array data on the right can also be processed similarly
Repeat the above steps,

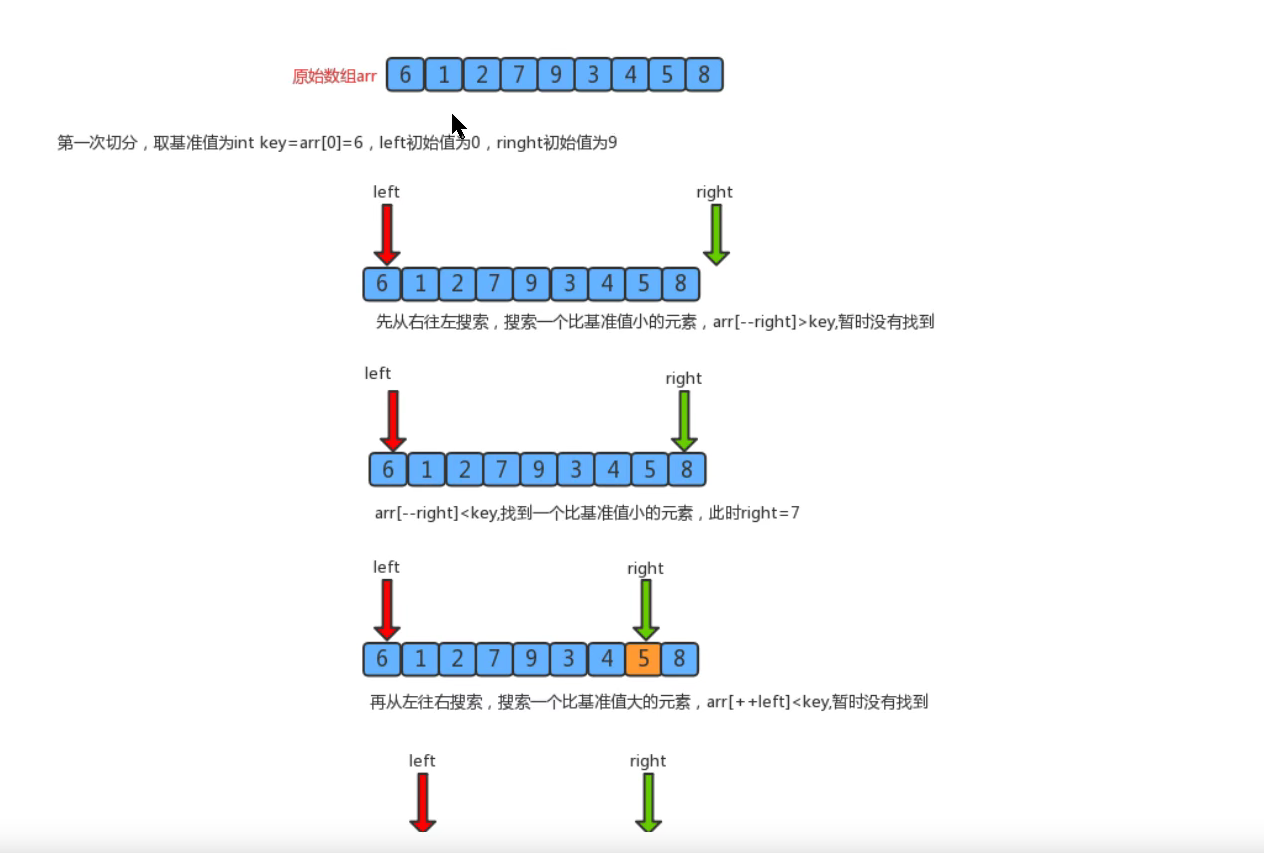
package sort;
/**
* Quick sort
*/
public class Quick {
//Auxiliary array needed for merge sort
private static Comparable[] assist;
/**
* Sort the elements in array a
*
* @param a
*/
public static void sort(Comparable[] a) {
int lo = 0;
int hi = a.length - 1;
sort(a, lo, hi);
}
/**
* Sort the elements from lo to hi in array a
*
* @param a
* @param lo
* @param hi
*/
public static void sort(Comparable[] a, int lo, int hi) {
//Security verification
if (hi <= lo) {
return;
}
//Group the elements in the array from lo index to hi index (left subgroup and right subgroup)
int partition = partition(a, lo, hi);//The returned index is the index of the boundary value of the group. Note that it is the index after the boundary value position transformation (the default boundary value is the first value of each subgroup)
//Order the left subgroup
sort(a, lo, partition - 1);
//Order the right subgroup
sort(a, partition + 1, hi);
}
/**
* Group the elements from lo to hi in array a and return the value corresponding to the grouping boundary
*
* @param a
* @param lo
* @param hi
*/
public static int partition(Comparable[] a, int lo, int hi) {
//Determine boundary value
Comparable key = a[lo];
//Define two pointers to point to the next position at the minimum index and the maximum index of the element to be segmented
int left = lo;
int right = hi + 1;
//segmentation
while (true) {
//Scan from right to left, move the right pointer, find an element with small score boundary value, and stop
while (less(key, a[--right])) {
if (right == lo) {
break;
}
}
//Scan from left to right, move the left pointer, find an element with a large score boundary value, and stop
while (less(a[++left],key)) {
if (left == right) {
break;
}
}
if (left>=right) {
break;
}else {
exch(a,left,right);
}
}
//Exchange boundary value
exch(a,lo,right);
return right;
}
/**
* Compare whether the v element is smaller than the w element
*
* @param v
* @param w
* @return
*/
public static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
/**
* Data element i,j exchange location
*
* @param a
* @param i
* @param j
*/
public static void exch(Comparable[] a, int i, int j) {
Comparable temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
Time complexity analysis:
Worst case: N^2
Average time complexity: O(nlogn)
According to the large o rule, the highest order term is retained, and the final time complexity is O(N^2)
2.4 stability of sorting
Stability of common sorting algorithms

The screenshots in this article are from station B video
Video resources: https://www.bilibili.com/video/BV1Cz411B7qd
Apply to w element
*
* @param v
* @param w
* @return
*/
public static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
/**
* Data element i,j exchange location
*
* @param a
* @param i
* @param j
*/
public static void exch(Comparable[] a, int i, int j) {
Comparable temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
### Time complexity analysis: Worst case scenario: N^2 Average time complexity: O(nlogn) According to big O rule, Retain the highest order term, The final time complexity is: O(N^2) ## 2.4 stability of sorting Stability of common sorting algorithms [External chain picture transfer...(img-NC8FUe2H-1641716367381)] The screenshots in this article are from B Station video Video resources: https://www.bilibili.com/video/BV1Cz411B7qd