SOLUTION NUMBER OF POJ_-EQUATION
Time limit 5000MS/Case memory 128MB/Case
Topic Description
A higher order equation of n variables is known: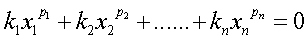
Among them: x1, x2,...,xn is an unknown number, k1,k2,...,kn is a coefficient, p1,p2,...pn is an index. And all the numbers in the equation are integers.
Assuming that the unknowns 1 <= Xi <= M, I = 1,, n, the number of integer solutions of the equation is obtained.
1 <= n <= 6;1 <= M <= 150. 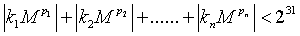
The number of integer solutions of the equation is less than 231.
In this question, the exponent Pi(i=1,2,...,n) is a positive integer.
Input format
Output format
sample input
3 150 1 2 -1 2 1 2
sample output
178
1<=M<=150,1<=N<=6,1<=X[i]<=M
----------------------------------------------------------
Topic analysis
Determine the way of thinking, because this problem is not good to establish mathematical problem solving model, so directly choose the upper enumeration algorithm.
Enumeration of six numbers to check the time complexity is O(M^6), the worst time complexity is O(150^6), can not pass this problem.
So we think of the idea of meeting in mid-use. First we enumerate the first three numbers, save the sum of the first three numbers, and then enumerate the last three numbers. Then we can get an ans by checking each sum with the previous sum.
Because the maximum number of sums generated in the first half is 150*150*150, we construct a hash table: hash[4000000].
----------------------------------------------------------
Code (enumeration process slag, good to run all test points at 1500ms)
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include <vector>
#define hashsize 4000003
using namespace std;
long long p[151][10];
struct node{
int value;
int count;
};
node h[hashsize];
bool used[hashsize];
int get_hash(int x)
{
int tmp=(abs(x))%hashsize;
while(used[tmp] && h[tmp].value!=x)
{
tmp++;
if(tmp>4000000) tmp%=hashsize;
}
return tmp;
}
int hash_count(int x)
{
int i=get_hash(x);
return h[i].count;
}
void hash_insert(int x)
{
int i=get_hash(x);
h[i].value=x;
used[i]=true;
h[i].count++;
}
int pow(int base,int power)
{
if(p[base][power]>=1) return p[base][power];
if(power==0) return 1;
long long temp=pow(base,power/2);
if(power%2==1) return p[base][power]=(temp*temp)*base;
else return p[base][power]=(temp*temp);
}
void calcpow()
{
for(int i=1;i<=150;i++) p[i][1]=i;
for(int i=1;i<=150;i++)
for(int j=2;j<=9;j++) p[i][j]=p[i][j-1]*i;
return;
}
void work()
{
int k[7],pow_up[7];
int n,m,ans=0,tempr,cnt;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d%d",&k[i],&pow_up[i]);
if(n==1)
{
for(int i=1;i<=m;i++)
{
if(pow(i,pow_up[1])*k[1]==0) ans++;
}
}
else if(n==2)
{
for(int i=1;i<=m;i++)
{
for(int j=1;j<=m;j++)
{
if(pow(i,pow_up[1])*k[1]+pow(j,pow_up[2])*k[2]==0) ans++;
}
}
}
else if(n==3)
{
for(int i=1;i<=m;i++)
{
for(int j=1;j<=m;j++)
{
for(int l=1;l<=m;l++)
{
if(pow(i,pow_up[1])*k[1]+pow(j,pow_up[2])*k[2]+pow(l,pow_up[3])*k[3]==0) ans++;
}
}
}
}
else if(n==4)
{
for(int i=1;i<=m;i++)
{
for(int j=1;j<=m;j++)
{
hash_insert(pow(i,pow_up[1])*k[1]+pow(j,pow_up[2])*k[2]);
}
}
for(int i=1;i<=m;i++)
{
for(int j=1;j<=m;j++)
{
ans+=hash_count(-(pow(i,pow_up[3])*k[3]+pow(j,pow_up[4])*k[4]));
}
}
}
else if(n==5)
{
for(int i=1;i<=m;i++)
{
for(int j=1;j<=m;j++)
{
hash_insert(pow(i,pow_up[1])*k[1]+pow(j,pow_up[2])*k[2]);
}
}
for(int i=1;i<=m;i++)
{
for(int j=1;j<=m;j++)
{
for(int l=1;l<=m;l++)
{
ans+=hash_count(-(pow(i,pow_up[4])*k[4]+pow(j,pow_up[5])*k[5]+pow(l,pow_up[3])*k[3]));
}
}
}
}
else if(n==6)
{
calcpow();
for(int i=1;i<=m;i++)
{
for(int j=1;j<=m;j++)
{
for(int l=1;l<=m;l++)
{
hash_insert(p[i][pow_up[1]]*k[1]+p[j][pow_up[2]]*k[2]+p[l][pow_up[3]]*k[3]);
}
}
}
for(int i=1;i<=m;i++)
{
for(int j=1;j<=m;j++)
{
for(int l=1;l<=m;l++)
{
ans+=hash_count(-(p[i][pow_up[4]]*k[4]+p[j][pow_up[5]]*k[5]+p[l][pow_up[6]]*k[6]));
}
}
}
}
printf("%d",ans);
return;
}
int main()
{
work();
return 0;
}