This topic is not difficult, but there is still something to learn to write simple and elegant code.

Topic 1

Force buckle

 

class Solution:
    def cellsInRange(self, s: str) -> List[str]:
        ans = []
        a,b,c,d = s[0],s[1],s[3],s[4]
        for i in range(ord(a), ord(c)+1):
            for j in range(int(b),int(d)+1):
                ans.append(chr(i)+str(j))
        return ans

Question 2:

Force buckle

AC code:

class Solution {
public:
    long long calc(long long l, long long r) {
        if(l>r) return 0;
        return (l+r)*(r-l+1)/2;
    }
    long long minimalKSum(vector<int>& nums, int k) {
        sort(nums.begin(), nums.end());
        long long ans = 0;
        if(nums[0] - 1 >= k) {
            return calc(1, k);
        } else {
            ans += calc(1, nums[0]-1);
            k -= nums[0]-1;
        }
        for(int i = 1; i<nums.size(); i++) {
            if(nums[i] - nums[i-1] <=1) continue;
            if(nums[i] - nums[i-1] - 1 <= k) {
                k -= nums[i] - nums[i-1] - 1;
                ans += calc(nums[i-1]+1, nums[i]-1);
            } else {
                ans += calc(nums[i-1]+1, nums[i-1]+1+k-1);
                k = 0;
                break;
            }
        }
        if(k>0) {
            ans += calc(nums[nums.size()-1]+1, nums[nums.size()-1]+k);
        }
        return ans;
    }
};

AC Code 2: (Sentinels are a great thing)

class Solution {
public:
    long long calc(long long l, long long r) {
        if(l>r) return 0;
        return (l+r)*(r-l+1)/2;
    }
    long long minimalKSum(vector<int>& nums, int k) {
        nums.push_back(0);nums.push_back(int(1e9) + 5000000);
        sort(nums.begin(), nums.end());
        long long ans = 0;
        
        for(int i = 1; i<nums.size(); i++) {
            if(nums[i] - nums[i-1] <=1) continue;
            if(nums[i] - nums[i-1] - 1 <= k) {
                k -= nums[i] - nums[i-1] - 1;
                ans += calc(nums[i-1]+1, nums[i]-1);
            } else {
                ans += calc(nums[i-1]+1, nums[i-1]+1+k-1);
                k = 0;
                break;
            }
        }
        return ans;
    }
};

AC code 3:

It only needs one summation formula of equal difference columns. Assume 1~K first, and then add it after traversing the array.

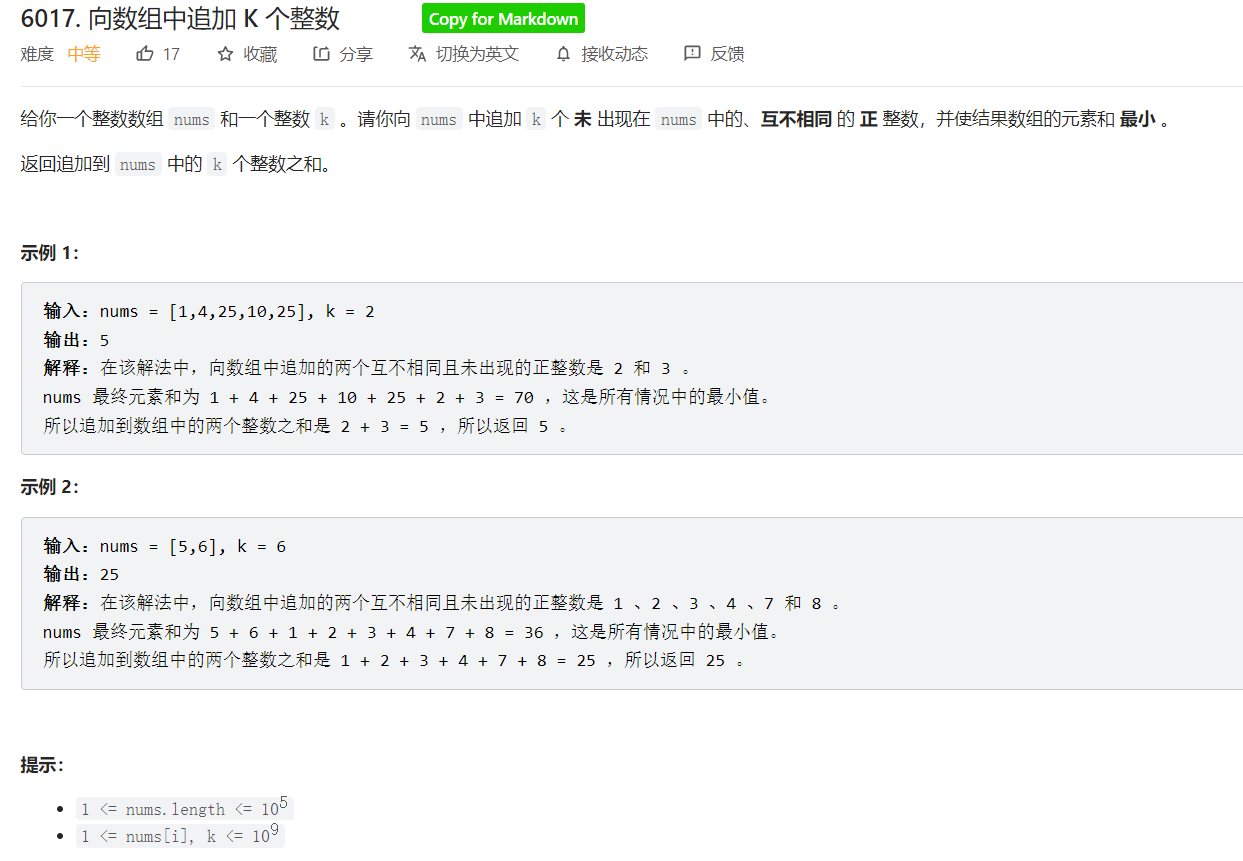
Question 3

Force buckle

Problem solving report:

I'm really writing junk code. First, the last for loop can be merged into the first one. Because he is a pointer, as long as new comes out, even if left and right are null, it's okay to modify them directly.

And it's really cool to write this in python, dict can replace everything here. Rewrite empty to py.

And in fact, set is not the best one to use here. Wouldn't it be good to add a vis array? Do not take a log.

But what I was thinking about was changing fa directly to map, but it wasn't easy to simplify because you wanted to find the node that existed but didn't appear as a child node.

AC code:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int fa[100005];
    TreeNode* tr[100005];
    TreeNode* createBinaryTree(vector<vector<int>>& descriptions) {
        set<int> ss;
        for(int i = 0; i<descriptions.size(); i++) {
            int f = descriptions[i][0];
            int s = descriptions[i][1];
            fa[s] = f;
            ss.insert(s);ss.insert(f);
            if(tr[s] == nullptr) tr[s] = new TreeNode(s);
            if(tr[f] == nullptr) tr[f] = new TreeNode(f); 
        }
        int root;
        for(auto x : ss) {
            if(fa[x] == 0) {
                root = x;break;
            }
        }
        for(int i = 0; i<descriptions.size(); i++) {
            int f = descriptions[i][0];
            int s = descriptions[i][1];
            if(descriptions[i][2] == 1) tr[f]->left = tr[s];
            else tr[f]->right = tr[s];
        }        
        return tr[root];
    }
};

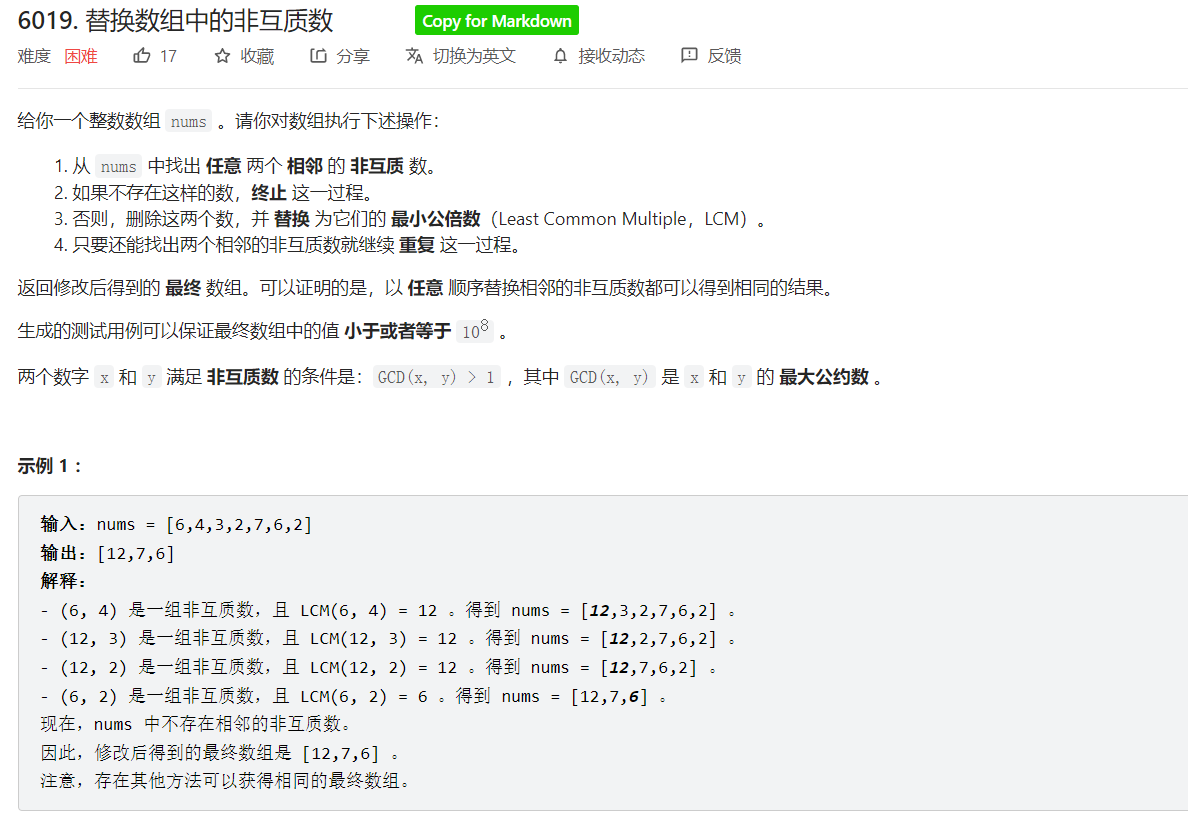
Question 4

Force buckle

 

Solution Report:

At first I left the question blank and did not see two adjacent nonreciprocal prime numbers to find. After half a day's thought, I came up with a solution to this "upgrade" topic. I will talk about it.

But if the question is adjacent, it will actually simplify a lot.

Neighboring problems can be considered by the stack. (just like bracket matching, etc.)

AC code:

class Solution {
public:
    long long gcd(long long  a, long long b) {
        return b==0?a:gcd(b,a%b);
    }
    long long lcm(long long a, long long b) {
        return a*b/gcd(a,b);
    }
    vector<int> replaceNonCoprimes(vector<int>& nums) {
        stack<int> sk;
        sk.push(nums[0]);
        for(int i = 1; i<nums.size(); i++) {
            sk.push(nums[i]);
            int t1 = sk.top();sk.pop();
            int t2 = sk.top();sk.pop();
            int flag = 0;
            while(gcd(t1, t2) != 1) {
                sk.push(lcm(t1, t2));
                if(sk.size() <= 1) {
                    flag = 1;
                    break;
                }
                t1 = sk.top();sk.pop();
                t2 = sk.top();sk.pop();
            }
            if(flag == 0) {
                sk.push(t2);sk.push(t1);
            }
        }
        vector<int> ans;
        while(sk.size()) {
            int x = sk.top();
            ans.push_back(x);sk.pop();
        }
        reverse(ans.begin(), ans.end());
        return ans;
    }
};

This question 1WA because sk. Size()<=1 break s but forgot to push in the removed element again.

Then 2WA writes: it actually only changes the pop outside. Think again about whether there is a similar situation that causes pops to forget to push. So you'll find that there's also inside while. Then you can change it all at once.

//Part of code for 2WA
        for(int i = 1; i<nums.size(); i++) {
            sk.push(nums[i]);
            int t1 = sk.top();sk.pop();
            int t2 = sk.top();sk.pop();
            if(gcd(t1, t2) != 1) {
            	while(gcd(t1, t2) != 1) {
	                sk.push(int(lcm(t1, t2)));
	                if(sk.size() <= 1) {
	                	break;
					}
	                t1 = sk.top();sk.pop();
	                t2 = sk.top();sk.pop();
	            }
			} else {
				sk.push(t2);sk.push(t1);
			}
        }

It's ugly, too. The stack problem can actually be written with a vector s, so that you don't have to go out of the stack and reverse it again at the end, and you don't have to go through every sk.top()sk.pop(), just take v[v.size()-1] and v[v.size()-2], so you don't have to push in if flag==0. That's ugly. See what people write.

class Solution {
public:
    int gcd(int x, int y) { return y ? gcd(y, x % y) : x; }
    
    vector<int> replaceNonCoprimes(vector<int>& nums) {
        int n = nums.size();
        vector<int> ans;
        for (int i = 0; i < n; ++i) {
            int t = nums[i];
            while (!ans.empty() && gcd(t, ans.back()) > 1) {
                t = t / gcd(t, ans.back()) * ans.back();
                ans.pop_back();
            }
            ans.push_back(t);
        }
        return ans;
    }
};