Solving combined Sudoku by backtracking method

Posted by byp on Mon, 08 Nov 2021 18:25:26 +0100

Solving combined Sudoku by backtracking method

1. Problem description

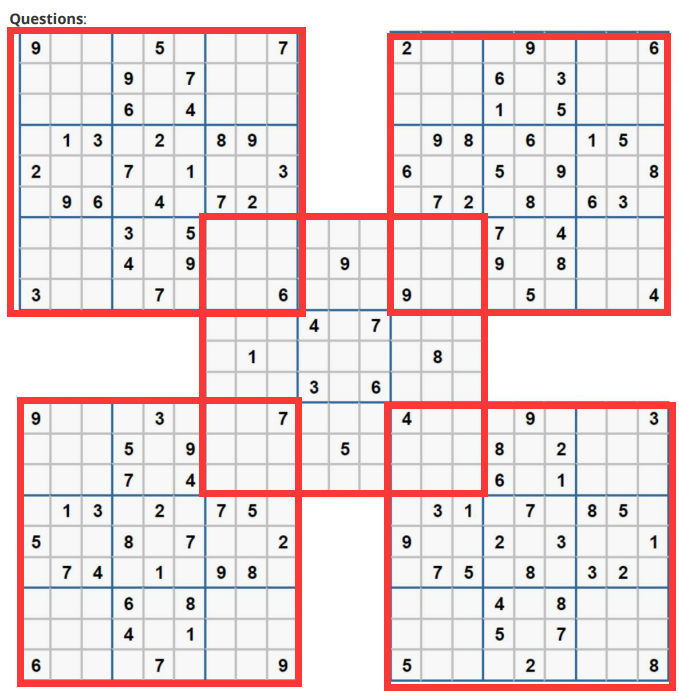
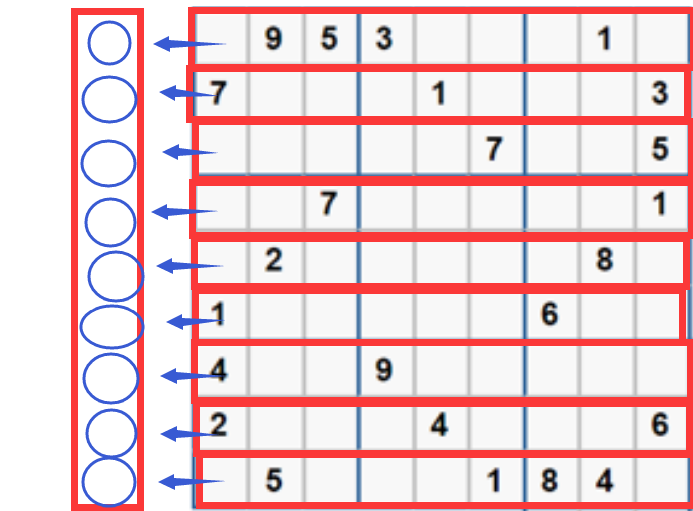
As shown in the figure above, in the red box of each 9 * 9, some numbers from 0 to 9 are filled in, and some are blank.

Fill in the blanks with numbers from 0 to 9 so that:

Each blue nine space cannot have duplicate numbers
Each line cannot have duplicate numbers
Each column cannot have duplicate numbers

2. Ideas and Implementation

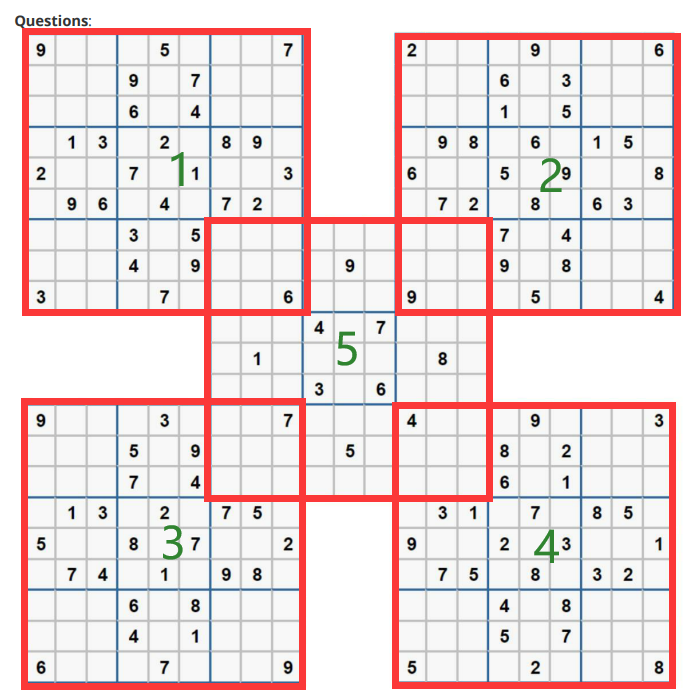
The whole problem can be divided into five sub problems, that is, the solution of five 9 * 9 Sudoku. The solution of the middle Sudoku depends on the solution results of the other four Sudoku.

The idea is very clear, that is, first solve the four Sudoku around, splice it into the middle Sudoku, and then solve it.

2.1 single Sudoku solution

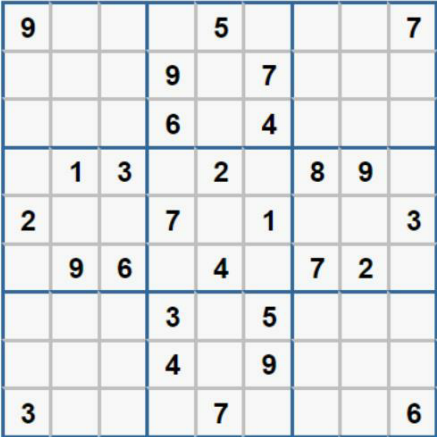
The number filling of each blank cell in Sudoku is constrained by its row, column and Jiugong cell. If you recalculate each time you fill in an empty white cell, there will be a lot of repeated calculations, and the time complexity is very high. Therefore, you can store the intermediate value and look it up in the table. The steps to solve a single Sudoku can be divided into:

Initialize intermediate value
Fill in a blank box
Update intermediate value
Is it the last empty white space
1. No, execute 2
2. It's over
Restore intermediate value

2.1.1 storage of Sudoku

Sudoku storage uses a 9 * 9 integer array to facilitate intermediate value calculation 2 n 2^n 2n for storage. 0 means no number has been filled in.
0 − > 2 0 = 0 ( 0000000000 ) 1 − > 2 1 = 2 ( 0000000010 ) 2 − > 2 2 = 4 ( 0000000100 ) 3 − > 2 3 = 8 ( 0000001000 ) 4 − > 2 4 = 16 ( 0000010000 ) 5 − > 2 5 = 32 ( 0000100000 ) 6 − > 2 6 = 64 ( 0001000000 ) 7 − > 2 7 = 128 ( 0010000000 ) 8 − > 2 8 = 256 ( 0100000000 ) 9 − > 2 9 = 512 ( 1000000000 ) \\ 0 -> 2^{0} = 0(0000000000) \\ 1 -> 2^{1} = 2(0000000010)\\ 2 -> 2^{2} = 4(0000000100)\\ 3 -> 2^{3} = 8(0000001000)\\ 4 -> 2^{4} = 16(0000010000)\\ 5 -> 2^{5} = 32(0000100000)\\ 6 -> 2^{6} = 64(0001000000)\\ 7 -> 2^{7} = 128(0010000000)\\ 8 -> 2^{8} = 256(0100000000)\\ 9 -> 2^{9} = 512(1000000000)\\ 0−>20=0(0000000000)1−>21=2(0000000010)2−>22=4(0000000100)3−>23=8(0000001000)4−>24=16(0000010000)5−>25=32(0000100000)6−>26=64(0001000000)7−>27=128(0010000000)8−>28=256(0100000000)9−>29=512(1000000000)

Set the conversion array, n u m [ n ] = 2 n num[n] = 2^n num[n]=2n .

int num[] = {0, 2, 4, 8, 16, 32, 64, 128, 256, 512};

Initialize Sudoku array:

int a[5][9][9] ={
		{
			{num[9], num[0], num[0], num[0], num[5], num[0], num[0], num[0], num[7]},
			{num[0], num[0], num[0], num[9], num[0], num[7], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[6], num[0], num[4], num[0], num[0], num[0]},
			{num[0], num[1], num[3], num[0], num[2], num[0], num[8], num[9], num[0]},
			{num[2], num[0], num[0], num[7], num[0], num[1], num[0], num[0], num[3]},
			{num[0], num[9], num[6], num[0], num[4], num[0], num[7], num[2], num[0]},
			{num[0], num[0], num[0], num[3], num[0], num[5], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[4], num[0], num[9], num[0], num[0], num[0]},
			{num[3], num[0], num[0], num[0], num[7], num[0], num[0], num[0], num[6]}
		},
		{
			{num[2], num[0], num[0], num[0], num[9], num[0], num[0], num[0], num[6]},
			{num[0], num[0], num[0], num[6], num[0], num[3], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[1], num[0], num[5], num[0], num[0], num[0]},
			{num[0], num[9], num[8], num[0], num[6], num[0], num[1], num[5], num[0]},
			{num[6], num[0], num[0], num[5], num[0], num[9], num[0], num[0], num[8]},
			{num[0], num[7], num[2], num[0], num[8], num[0], num[6], num[3], num[0]},
			{num[0], num[0], num[0], num[7], num[0], num[4], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[9], num[0], num[8], num[0], num[0], num[0]},
			{num[9], num[0], num[0], num[0], num[5], num[0], num[0], num[0], num[4]}
		},
		{
			{num[9], num[0], num[0], num[0], num[3], num[0], num[0], num[0], num[7]},
			{num[0], num[0], num[0], num[5], num[0], num[9], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[7], num[0], num[4], num[0], num[0], num[0]},
			{num[0], num[1], num[3], num[0], num[2], num[0], num[7], num[5], num[0]},
			{num[5], num[0], num[0], num[8], num[0], num[7], num[0], num[0], num[2]},
			{num[0], num[7], num[4], num[0], num[1], num[0], num[9], num[8], num[0]},
			{num[0], num[0], num[0], num[6], num[0], num[8], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[4], num[0], num[1], num[0], num[0], num[0]},
			{num[6], num[0], num[0], num[0], num[7], num[0], num[0], num[0], num[9]}
		},
		{
			{num[4], num[0], num[0], num[0], num[9], num[0], num[0], num[0], num[3]},
			{num[0], num[0], num[0], num[8], num[0], num[2], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[6], num[0], num[1], num[0], num[0], num[0]},
			{num[0], num[3], num[1], num[0], num[7], num[0], num[8], num[5], num[0]},
			{num[9], num[0], num[0], num[2], num[0], num[3], num[0], num[0], num[1]},
			{num[0], num[7], num[5], num[0], num[8], num[0], num[3], num[2], num[0]},
			{num[0], num[0], num[0], num[4], num[0], num[8], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[5], num[0], num[7], num[0], num[0], num[0]},
			{num[5], num[0], num[0], num[0], num[2], num[0], num[0], num[0], num[8]}
		},
		{
			{num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[0], num[9], num[0], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[4], num[0], num[7], num[0], num[0], num[0]},
			{num[0], num[1], num[0], num[0], num[0], num[0], num[0], num[8], num[0]},
			{num[0], num[0], num[0], num[3], num[0], num[6], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[0], num[5], num[0], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0]}
		}
	};

2.1.2 calculation of intermediate value

The calculation of intermediate value includes:

The middle value of the nine palaces
Middle value of row and column

2.1.2.1 calculation of intermediate value of Jiugong grid

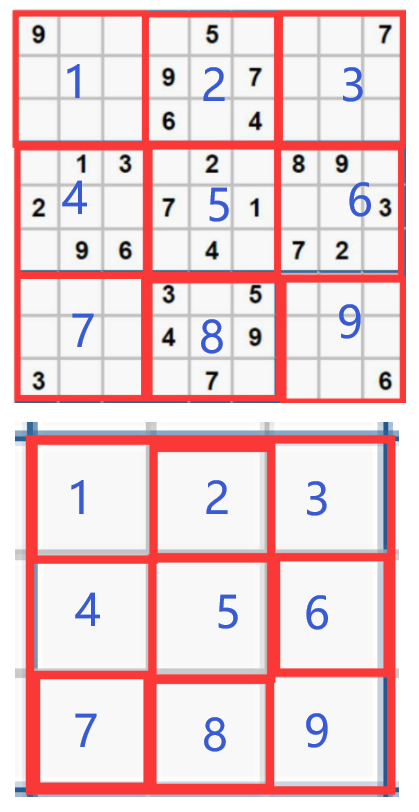
For the whole Sudoku, calculate the middle value of the nine squares. from 2.11 It can be seen that the storage of numbers in Sudoku adopts 2 n 2^n 2n. All the numbers of a single Jiugong lattice are or calculated by bits to obtain the result s s s， s s In the lower 10 bit binary representation of s, the number of bits is recorded as i i I (digits start from 0). If No i i If the i bit is 0, it means to fill in a number i i i no conflict.

//Calculate the number of 1 records 1-9 in the binary system 
//Start (i, f) 
int cal_smallGrid(int a[9][9], int i, int f){
	int s = 0;
	for(int g = 0; g < 3; g++){
		for(int h = 0; h < 3; h++){
			s |= a[i + g][f + h];
		}
	}
	return s;
}

2.1.2.2 calculation of row and column intermediate values

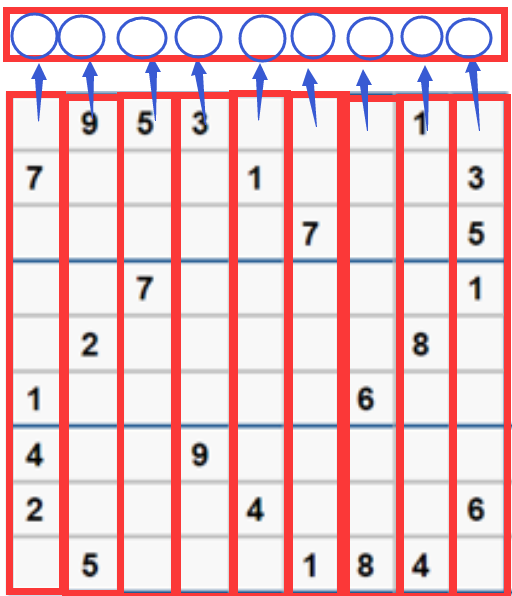
Same principle Jiugong grid middle value All numbers in each column and row are or calculated by bits.

//  tag 0 - Fixed F 1 - Fixed i 
// kind 0 first operation 1 second operation 
int cal_ranks(int a[9][9], int i, int f, int tag, int kind){
	int s = 0;
	for(int n = 0; n < 9; n++){
		if(kind == 0){
			if(tag == 0){
				s |= a[i + n][f];
			}else{
				s |= a[i][f + n];
			}
		}else{
			if(tag == 0){
				if(a[i + n][f] > 0) s++;
			}else{
				if(a[i][f + n] > 0) s++;
			}
		}
	}
	return s;
}

2.1.2.3 initializing intermediate values

use 3 ∗ 3 3*3 The shaping array of 3 * 3 stores the middle value of the Jiugong lattice, 2 ∗ 9 2*9 The shaping array of 2 * 9 stores the middle value of the row and column, in which the first row stores the middle value of the column and the second row stores the middle value of the row.

//initialization 
void initial(int a[9][9], int b[3][3], int c[2][9]){
	
	for(int i = 0, g = 0; i < 3; i++, g += 3){
		for(int f = 0, h = 0; f < 3; f++, h += 3){
			b[i][f] = cal_smallGrid(a, g, h);
		}
	}
	
	for(int i = 0; i < 2; i++){
		for(int f = 0; f < 9; f++){
			if(i == 0){
				c[i][f] = cal_ranks(a, 0, f, i, 0);
			}else{
				c[i][f] = cal_ranks(a, f, 0, i, 0);
			}
		}
	}
    
}

2.1.2.4 update and restore intermediate values

When a number is inserted or removed from a blank space, the middle value of its row and column will change. Therefore, the intermediate value needs to be updated and restored.

When inserting a number, the number is bitwise or calculated with the corresponding row, column and the middle value of the Jiugong grid.

When removing a number, reverse the number to the corresponding row and column, and perform bitwise sum operation on the middle value of Jiugong lattice.

// Update after changing (i, f) 
//tag = 0 -- update 
//tag = 1 -- Restore
void update(int i, int f, int n, int b[3][3], int c[2][9], int tag){
	
	int index_i = i / 3;
	int index_f = f / 3;
	
	if(tag == 0){
		b[index_i][index_f] |= n;
		c[0][f] |= n;
		c[1][i] |= n;
	}else{
		n = ~n;
		b[index_i][index_f] &= n;
		c[0][f] &= n;
		c[1][i] &= n;
	}
	
}

2.1.3 single Sudoku solving algorithm

Solving the whole Sudoku can be converted to solving the value of each blank lattice, and the possible value of the blank lattice depends on the middle value of its Jiugong lattice, row and column. It can be solved by backtracking recursion until the whole Sudoku is solved.

2.1.3.1 define data structure

In order to use the queue in the STl library, define a big that stores a single Sudoku_ A structure and the total of the saved results_ A structure.

Four queues are used to store the results of the four Sudoku around, which is convenient for the subsequent combination to solve the fifth Sudoku.

struct big_A{
	int a[9][9];
};

struct total_A{
	big_A a[5];
};

total_A totalA;
queue<big_A> Bigqueue1;
queue<big_A> Bigqueue2;
queue<big_A> Bigqueue3;
queue<big_A> Bigqueue4;

2.1.3.2 backtracking solution

According to the Sudoku table, Jiugong grid and row and column intermediate variables, you can start to solve Sudoku.

The solution process is as follows:

Start: find the next cell

If the number of Sudoku cells is exceeded, it means to go to the end and save the results
Not exceeded
- The cell is blank. Try to fill in all possible numbers according to the intermediate value, update the intermediate value, jump to the beginning, restore the intermediate value, and mark that no numbers are inserted in this cell.
- The cell has been filled with numbers. Jump to the beginning

A number is available n n n represents the cell being solved, then its rows and columns in the two-dimensional Sudoku array are i = n / 9 i = n/9 i=n/9 and f = n % 9 f = n\%9 f=n%9. The subscript of the corresponding Jiugong lattice intermediate variable is [ i / 3 ] [ f / 3 ] [i/3][f/3] [i/3][f/3], the corresponding column intermediate variable subscript is [ 0 ] [ f ] [0][f] [0][f], the subscript of the corresponding line intermediate variable is [ 1 ] [ i ] [1][i] [1][i]. Carry out bitwise OR operation on Jiugong lattice variables, row variables and column variables, and then divide by 2 (remove zero). The number of 0 in the lower 9-bit binary corresponds to the possible value.

//Tag solve the tag+1 Sudoku 
int backTrack(int a[9][9], int b[3][3], int c[2][9], int n, int tag){
	//Export 
	if(n == 81){
		big_A A;
		memcpy(A.a, a, 81 * sizeof(int));
		switch(tag){
			case 0: Bigqueue1.push(A); break;
			case 1: Bigqueue2.push(A); break;
			case 2: Bigqueue3.push(A); break;
			case 3: Bigqueue4.push(A); break;
			case 4: 
				totalA.a[4] =  A; 
				cout << "finish!" << endl; 
				for(int i = 0; i < 5; i++){
					cout << i << " " << endl;
					for(int f = 0; f < 9; f++){
						for(int g = 0; g < 9; g++){
							cout << tab(totalA.a[i].a[f][g]) << " ";
						}
						cout << endl;
					}
					cout << endl << endl;
				}
				break;
			default: cout << "Error!" << endl; break;
		}
		
	}else{
		int index_i, index_f;
		index_i = n / 9;
		index_f = n % 9;
		
		if(a[index_i][index_f] == 0){
			int mid = b[index_i / 3][ index_f / 3];
			int lie = c[0][index_f];
			int hang = c[1][index_i];
			int s = mid | lie | hang;
            
			s /= 2;
			for(int i = 1; i <= 9; i++){
				int yu = s % 2;
				if(yu == 0){
					a[index_i][index_f] = num[i];
					update(index_i, index_f, num[i], b, c, 0);
					backTrack(a, b, c, n + 1, tag);
					update(index_i, index_f, num[i], b, c, 1);
					a[index_i][index_f] = 0;
				}
				s /= 2;
			}
		}else if(a[index_i][index_f] > 0){
			backTrack(a, b, c, n + 1, tag);
		}
	}
}

2.2 solving the last Sudoku by combination

Can be based on 2.1 The solution of Sudoku No. 1-4 can be based on the results of Sudoku No. 1-4. That is, fill the Sudoku array in the middle according to the result, judge the legitimacy, and then solve the Sudoku.

2.2.1 Sudoku in the middle

Fill in Sudoku No. 5 according to the results of Sudoku No. 1 ~ 4:

The lower right square of Sudoku No. 1 fills the upper left square of Sudoku No. 5.
The lower left square of Sudoku No. 2 fills the upper right square of Sudoku No. 5.
The upper right grid of Sudoku No. 3 fills the lower left grid of Sudoku No. 5.
The upper left square of Sudoku No. 4 fills the lower right square of Sudoku No. 5.

// Fill a1 in A2 tag+1 -- the tag+1 matrix 
void fill(int a1[9][9], int a2[9][9], int tag){
	int i1, f1, i2, f2;
	switch(tag){
		case 0: 
		i1 = f1 = 6;
		i2 = f2 = 0;
		break;
		case 1: 
		i1 = f2 = 6;
		f1 = i2 = 0;
		break;
		case 2: 
		i1 = f2 = 0;
		f1 = i2 = 6;
		break;
		case 3: 
		i1 = f1 = 0;
		i2 = f2 = 6;
		break;
		default: cout << "Error!" << endl; break;
	}
	for(int i = 0; i < 3; i++){
		for(int f = 0; f < 3; f++){
			a2[i2 + i][f2 + f] = a1[i1 + i][f1 + f];
		}
	}
}

2.2.2 judging the legitimacy of combined Sudoku

The filling is combined into No. 5 Sudoku, which may produce the same number in the same row or column. Repeated judgment is required to check the legitimacy.

yes 2.1.2.2 calculation of row and column intermediate values as well as 2.1.2.3 initializing intermediate values Through improvement, we can judge the legitimacy of Sudoku combination.

When calculating row, column bitwise OR operation:

Or operation between the current number and the previous result
- Current number is 0, continue
- The current number is not 0, or the result of the operation
  - If the result is the same as the previous result, there must be duplicate numbers. End
  - The results are different from the previous results. Continue

//  tag 0 - Fixed F 1 - Fixed i 
// kind 0 first operation 1 second operation 
int cal_ranks(int a[9][9], int i, int f, int tag, int kind, int &ret){
	int s = 0;
	int pre_s = s;
	ret = 1;
	for(int n = 0; n < 9; n++){
		if(kind == 0){
			if(tag == 0){
				if(a[i + n][f] > 0){
					s |= a[i + n][f];
					if(s == pre_s){
						ret = 0;
						return s;
					}
				}
			}else{
				if(a[i][f + n] > 0){
					s |= a[i][f + n];
					if(s == pre_s){
						ret = 0;	
						return s;
					}
				}
			}
			pre_s = s;
		}else{
			if(tag == 0){
				if(a[i + n][f] > 0) s++;
			}else{
				if(a[i][f + n] > 0) s++;
			}
		}
	}
	return s;
}
//initialization 
int initial(int a[9][9], int b[3][3], int c[2][9]){
	//
	for(int i = 0, g = 0; i < 3; i++, g += 3){
		for(int f = 0, h = 0; f < 3; f++, h += 3){
			b[i][f] = cal_smallGrid(a, g, h);
//			cout << b[i][f] << "  ";
		}
//		cout << endl;
	}
	int ret = 1;
	for(int i = 0; i < 2; i++){
		for(int f = 0; f < 9; f++){
			if(i == 0){
				c[i][f] = cal_ranks(a, 0, f, i, 0, ret);
			}else{
				c[i][f] = cal_ranks(a, f, 0, i, 0, ret);
			}
			if(ret == 0) return 0;
//			cout << c[i][f] << "  ";
		}
//		cout << endl << endl;
	}
	return ret;
}

2.2.3 combined solution algorithm

from 2.1.3 single Sudoku solving algorithm It can be seen that the results of No. 1 ~ 4 Sudoku are stored in four queues respectively, taken out and filled into No. 5 Sudoku, judged the legitimacy, solved No. 5 Sudoku with a single Sudoku solving algorithm, and finally saved the results.

	big_A A1, A2, A3, A4;
	int n1, n2, n3, n4;
	n1 = Bigqueue1.size();
	n2 = Bigqueue2.size();
	n3 = Bigqueue3.size();
	n4 = Bigqueue4.size();
	cout << n1 << " " << n2 << " " << n3 << " " << n4 << endl;

	for(int i = 0; i < n1; i++){
		cout << i << endl;
		A1 = Bigqueue1.front();
		Bigqueue1.pop();
		for(int f = 0; f < n2; f++){
			A2 = Bigqueue2.front();
			Bigqueue2.pop();
			for(int g = 0; g < n3; g++){
				A3 = Bigqueue3.front();
				Bigqueue3.pop();
				for(int h = 0; h < n4; h++){
					A4 = Bigqueue4.front();
					Bigqueue4.pop();
					
					int num = sizeof(total_A) / 4;
					totalA.a[0] = A1;
					totalA.a[1] = A2;
					totalA.a[2] = A3;
					totalA.a[3] = A4;
					for(int i = 0; i < 4; i++){
						fill(totalA.a[i].a, a[4], i);
					}
					
					int ret = initial(a[4], b, c);
					if(ret == 1){
						backTrack(a[4], b, c, 0, 4);
					}
					
					Bigqueue4.push(A4);
				}
				Bigqueue3.push(A3);
			}
			Bigqueue2.push(A2);
		}
	}

3. Experimental results

3.1 results of the first question

In the first problem, the possible situations of Sudoku No. 1 ~ 4 are 511143250444 respectively. The combination solution has a huge amount of calculation, and the results need to be obtained at the hour level. The results are as follows:

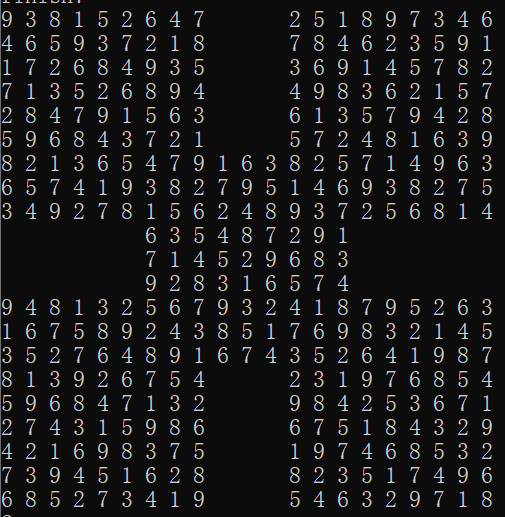
3.2 results of the second question

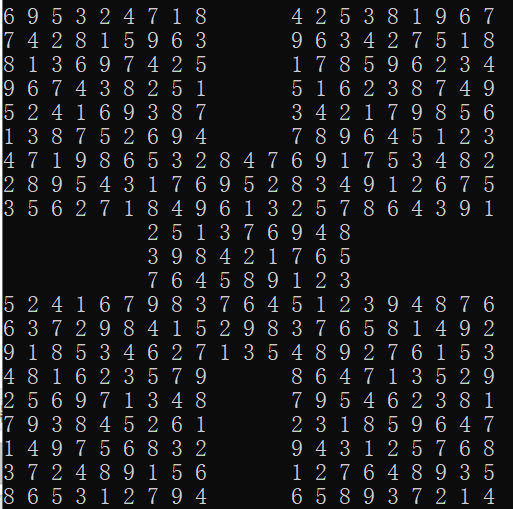
Second question:

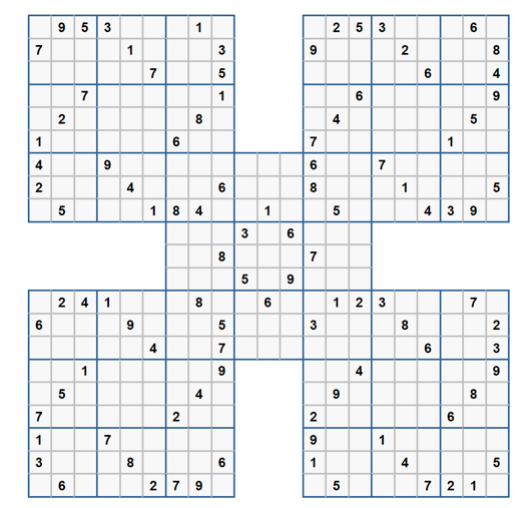
In the second problem, the possible situations of Sudoku No. 1 ~ 4 are 72, 44 and 7211 respectively. The combination solution has a moderate amount of calculation and can get the results at the second level. The results are as follows:

4. Complete code

#include <bits/stdc++.h>

using namespace std;
const int N = 0x3fe;

struct big_A{
	int a[9][9];
};

struct total_A{
	big_A a[5];
};

total_A totalA;
queue<big_A> Bigqueue1;
queue<big_A> Bigqueue2;
queue<big_A> Bigqueue3;
queue<big_A> Bigqueue4;

int num[] = {0, 2, 4, 8, 16, 32, 64, 128, 256, 512};


//transformation 
int tab(int x){
	int y = x / 2;
	for(int i = 1; i <= 9; i++){
		int yu = y % 2;
		if(yu == 1) return i;
		y /= 2;
	}
}


void cover(int x[21][21], int a[9][9], int index_i, int index_f){
	for(int i = 0; i < 9; i++){
		for(int f = 0; f < 9; f++){
			x[i + index_i][f + index_f] = tab(a[i][f]);
		}
	}
}
void show(){
	int x[21][21];
	memset(x, 0, sizeof(int) * 21 *21);
	int y[5][2] = {
		{0, 0},
		{0, 12},
		{12, 0},
		{12, 12},
		{6, 6}
	};
	for(int i = 0; i < 5; i++){
		cover(x, totalA.a[i].a, y[i][0], y[i][1]);
	}
	
	for(int i = 0; i < 21; i++){
		for(int f = 0; f < 21; f++){
			if(x[i][f] > 0){
				cout << x[i][f] << " ";
			}else{
				cout << "  ";
			}
			
		}
		cout << endl;
	}
}
	
	
	

//Calculate the number of 1 records 1-9 in the binary system 
//Start (i, f) 
int cal_smallGrid(int a[9][9], int i, int f){
	int s = 0;
	for(int g = 0; g < 3; g++){
		for(int h = 0; h < 3; h++){
			s |= a[i + g][f + h];
		}
	}
	return s;
}

//  tag 0 - Fixed F 1 - Fixed i 
// kind 0 first operation 1 second operation 
int cal_ranks(int a[9][9], int i, int f, int tag, int kind, int &ret){
	int s = 0;
	int pre_s = s;
	ret = 1;
	for(int n = 0; n < 9; n++){
		if(kind == 0){
			if(tag == 0){
				if(a[i + n][f] > 0){
					s |= a[i + n][f];
					if(s == pre_s){
						ret = 0;
						return s;
					}
				}
			}else{
				if(a[i][f + n] > 0){
					s |= a[i][f + n];
					if(s == pre_s){
						ret = 0;	
						return s;
					}
				}
			}
			pre_s = s;
		}else{
			if(tag == 0){
				if(a[i + n][f] > 0) s++;
			}else{
				if(a[i][f + n] > 0) s++;
			}
		}
	}
	return s;
}

//initialization 
int initial(int a[9][9], int b[3][3], int c[2][9]){
	//
	for(int i = 0, g = 0; i < 3; i++, g += 3){
		for(int f = 0, h = 0; f < 3; f++, h += 3){
			b[i][f] = cal_smallGrid(a, g, h);
		}
	}
	int ret = 1;
	for(int i = 0; i < 2; i++){
		for(int f = 0; f < 9; f++){
			if(i == 0){
				c[i][f] = cal_ranks(a, 0, f, i, 0, ret);
			}else{
				c[i][f] = cal_ranks(a, f, 0, i, 0, ret);
			}
			if(ret == 0) return 0;
		}
	}
	return ret;
}

// Update after changing (i, f) 
//tag = 0 -- update 
//tag = 1 -- Restore
void update(int i, int f, int n, int b[3][3], int c[2][9], int tag){
	
	int index_i = i / 3;
	int index_f = f / 3;
	
	if(tag == 0){
		b[index_i][index_f] |= n;
		c[0][f] |= n;
		c[1][i] |= n;
	}else{
		n = ~n;
		b[index_i][index_f] &= n;
		c[0][f] &= n;
		c[1][i] &= n;
	}
	
}



//to flash back 
//Tag tag + 1 
int backTrack(int a[9][9], int b[3][3], int c[2][9], int n, int tag){
	//Export 
	if(n == 81){

		big_A A;
		memcpy(A.a, a, 81 * sizeof(int));
		switch(tag){
			case 0: Bigqueue1.push(A); break;
			case 1: Bigqueue2.push(A); break;
			case 2: Bigqueue3.push(A); break;
			case 3: Bigqueue4.push(A); break;
			case 4: 
				totalA.a[4] =  A; 
				cout << "finish!" << endl; 
				show();
				break;
			default: cout << "Error!" << endl; break;
		}
		
	}else{
		int index_i, index_f;
		index_i = n / 9;
		index_f = n % 9;
		
		if(a[index_i][index_f] == 0){
			int mid = b[index_i / 3][ index_f / 3];
			int lie = c[0][index_f];
			int hang = c[1][index_i];
			
			int s = mid | lie | hang;
			s /= 2;
			for(int i = 1; i <= 9; i++){
				int yu = s % 2;
				if(yu == 0){
					a[index_i][index_f] = num[i];
					update(index_i, index_f, num[i], b, c, 0);
					backTrack(a, b, c, n + 1, tag);
					update(index_i, index_f, num[i], b, c, 1);
					a[index_i][index_f] = 0;
				}
				s /= 2;
				
			}
		}else if(a[index_i][index_f] > 0){
			backTrack(a, b, c, n + 1, tag);
		}
	}
}

// Fill a1 in A2 tag+1 -- the tag+1 matrix 
void fill(int a1[9][9], int a2[9][9], int tag){
	int i1, f1, i2, f2;
	switch(tag){
		case 0: 
		i1 = f1 = 6;
		i2 = f2 = 0;
		break;
		case 1: 
		i1 = f2 = 6;
		f1 = i2 = 0;
		break;
		case 2: 
		i1 = f2 = 0;
		f1 = i2 = 6;
		break;
		case 3: 
		i1 = f1 = 0;
		i2 = f2 = 6;
		break;
		default: cout << "Error!" << endl; break;
	}
	for(int i = 0; i < 3; i++){
		for(int f = 0; f < 3; f++){
			a2[i2 + i][f2 + f] = a1[i1 + i][f1 + f];
		}
	}
}
int count_num(int x){
	int s = 0;
	int mid = x / 2;
	for(int g = 1; g <= 9; g++){
		if(mid % 2 == 1) s++;
		mid /= 2;
	}
	return s;
}

int judge(int a[9][9], int c[2][9]){

	int x;
	for(int i = 0; i < 2; i++){
		for(int f = 0; f < 9; f++){
			if(i == 0){
				int num = cal_ranks(a, 0, f, i, 1, x);
				int s = count_num(c[i][f]);
				if(s != num) return -1;
			}else{
				int num = cal_ranks(a, f, 0, i, 1, x);
				int s = count_num(c[i][f]);
				if(s != num) return -1;
			}
		}
	}
	return 1;
}


int main(){

//	int a[5][9][9] ={
//		{
//			{num[0], num[9], num[5], num[3], num[0], num[0], num[0], num[1], num[0]},
//			{num[7], num[0], num[0], num[0], num[1], num[0], num[0], num[0], num[3]},
//			{num[0], num[0], num[0], num[0], num[0], num[7], num[0], num[0], num[5]},
//			{num[0], num[0], num[7], num[0], num[0], num[0], num[0], num[0], num[1]},
//			{num[0], num[2], num[0], num[0], num[0], num[0], num[0], num[8], num[0]},
//			{num[1], num[0], num[0], num[0], num[0], num[0], num[6], num[0], num[0]},
//			{num[4], num[0], num[0], num[9], num[0], num[0], num[0], num[0], num[0]},
//			{num[2], num[0], num[0], num[0], num[4], num[0], num[0], num[0], num[6]},
//			{num[0], num[5], num[0], num[0], num[0], num[1], num[8], num[4], num[0]}
//		},
//		{
//			{num[0], num[2], num[5], num[3], num[0], num[0], num[0], num[6], num[0]},
//			{num[9], num[0], num[0], num[0], num[2], num[0], num[0], num[0], num[8]},
//			{num[0], num[0], num[0], num[0], num[0], num[6], num[0], num[0], num[4]},
//			{num[0], num[0], num[6], num[0], num[0], num[0], num[0], num[0], num[9]},
//			{num[0], num[4], num[0], num[0], num[0], num[0], num[0], num[5], num[0]},
//			{num[7], num[0], num[0], num[0], num[0], num[0], num[1], num[0], num[0]},
//			{num[6], num[0], num[0], num[7], num[0], num[0], num[0], num[0], num[0]},
//			{num[8], num[0], num[0], num[0], num[1], num[0], num[0], num[0], num[5]},
//			{num[0], num[5], num[0], num[0], num[0], num[4], num[3], num[9], num[0]}
//		},
//		{
//			{num[0], num[2], num[4], num[1], num[0], num[0], num[0], num[8], num[0]},
//			{num[6], num[0], num[0], num[0], num[9], num[0], num[0], num[0], num[5]},
//			{num[0], num[0], num[0], num[0], num[0], num[4], num[0], num[0], num[7]},
//			{num[0], num[0], num[1], num[0], num[0], num[0], num[0], num[0], num[9]},
//			{num[0], num[5], num[0], num[0], num[0], num[0], num[0], num[4], num[0]},
//			{num[7], num[0], num[0], num[0], num[0], num[0], num[2], num[0], num[0]},
//			{num[1], num[0], num[0], num[7], num[0], num[0], num[0], num[0], num[0]},
//			{num[3], num[0], num[0], num[0], num[8], num[0], num[0], num[0], num[6]},
//			{num[0], num[6], num[0], num[0], num[0], num[2], num[7], num[9], num[0]}
//		},
//		{
//			{num[0], num[1], num[2], num[3], num[0], num[0], num[0], num[7], num[0]},
//			{num[3], num[0], num[0], num[0], num[8], num[0], num[0], num[0], num[2]},
//			{num[0], num[0], num[0], num[0], num[0], num[6], num[0], num[0], num[3]},
//			{num[0], num[0], num[4], num[0], num[0], num[0], num[0], num[0], num[9]},
//			{num[0], num[9], num[0], num[0], num[0], num[0], num[0], num[8], num[0]},
//			{num[2], num[0], num[0], num[0], num[0], num[0], num[6], num[0], num[0]},
//			{num[9], num[0], num[0], num[1], num[0], num[0], num[0], num[0], num[0]},
//			{num[1], num[0], num[0], num[0], num[4], num[0], num[0], num[0], num[5]},
//			{num[0], num[5], num[0], num[0], num[0], num[7], num[2], num[1], num[0]}
//		},
//		{
//			{num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0]},
//			{num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0]},
//			{num[0], num[0], num[0], num[0], num[1], num[0], num[0], num[0], num[0]},
//			{num[0], num[0], num[0], num[3], num[0], num[6], num[0], num[0], num[0]},
//			{num[0], num[0], num[8], num[0], num[0], num[0], num[7], num[0], num[0]},
//			{num[0], num[0], num[0], num[5], num[0], num[9], num[0], num[0], num[0]},
//			{num[0], num[0], num[0], num[0], num[6], num[0], num[0], num[0], num[0]},
//			{num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0]},
//			{num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0]}
//		}
//	};
	int a[5][9][9] ={
		{
			{num[9], num[0], num[0], num[0], num[5], num[0], num[0], num[0], num[7]},
			{num[0], num[0], num[0], num[9], num[0], num[7], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[6], num[0], num[4], num[0], num[0], num[0]},
			{num[0], num[1], num[3], num[0], num[2], num[0], num[8], num[9], num[0]},
			{num[2], num[0], num[0], num[7], num[0], num[1], num[0], num[0], num[3]},
			{num[0], num[9], num[6], num[0], num[4], num[0], num[7], num[2], num[0]},
			{num[0], num[0], num[0], num[3], num[0], num[5], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[4], num[0], num[9], num[0], num[0], num[0]},
			{num[3], num[0], num[0], num[0], num[7], num[0], num[0], num[0], num[6]}
		},
		{
			{num[2], num[0], num[0], num[0], num[9], num[0], num[0], num[0], num[6]},
			{num[0], num[0], num[0], num[6], num[0], num[3], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[1], num[0], num[5], num[0], num[0], num[0]},
			{num[0], num[9], num[8], num[0], num[6], num[0], num[1], num[5], num[0]},
			{num[6], num[0], num[0], num[5], num[0], num[9], num[0], num[0], num[8]},
			{num[0], num[7], num[2], num[0], num[8], num[0], num[6], num[3], num[0]},
			{num[0], num[0], num[0], num[7], num[0], num[4], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[9], num[0], num[8], num[0], num[0], num[0]},
			{num[9], num[0], num[0], num[0], num[5], num[0], num[0], num[0], num[4]}
		},
		{
			{num[9], num[0], num[0], num[0], num[3], num[0], num[0], num[0], num[7]},
			{num[0], num[0], num[0], num[5], num[0], num[9], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[7], num[0], num[4], num[0], num[0], num[0]},
			{num[0], num[1], num[3], num[0], num[2], num[0], num[7], num[5], num[0]},
			{num[5], num[0], num[0], num[8], num[0], num[7], num[0], num[0], num[2]},
			{num[0], num[7], num[4], num[0], num[1], num[0], num[9], num[8], num[0]},
			{num[0], num[0], num[0], num[6], num[0], num[8], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[4], num[0], num[1], num[0], num[0], num[0]},
			{num[6], num[0], num[0], num[0], num[7], num[0], num[0], num[0], num[9]}
		},
		{
			{num[4], num[0], num[0], num[0], num[9], num[0], num[0], num[0], num[3]},
			{num[0], num[0], num[0], num[8], num[0], num[2], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[6], num[0], num[1], num[0], num[0], num[0]},
			{num[0], num[3], num[1], num[0], num[7], num[0], num[8], num[5], num[0]},
			{num[9], num[0], num[0], num[2], num[0], num[3], num[0], num[0], num[1]},
			{num[0], num[7], num[5], num[0], num[8], num[0], num[3], num[2], num[0]},
			{num[0], num[0], num[0], num[4], num[0], num[8], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[5], num[0], num[7], num[0], num[0], num[0]},
			{num[5], num[0], num[0], num[0], num[2], num[0], num[0], num[0], num[8]}
		},
		{
			{num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[0], num[9], num[0], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[4], num[0], num[7], num[0], num[0], num[0]},
			{num[0], num[1], num[0], num[0], num[0], num[0], num[0], num[8], num[0]},
			{num[0], num[0], num[0], num[3], num[0], num[6], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[0], num[5], num[0], num[0], num[0], num[0]},
			{num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0], num[0]}
		}
	};
	

	int b[3][3];
	int c[2][9];
	
	for(int i = 0; i < 4; i++){
		initial(a[i], b, c);
		backTrack(a[i], b, c, 0, i);
	}

	big_A A1, A2, A3, A4;
	int n1, n2, n3, n4;
	n1 = Bigqueue1.size();
	n2 = Bigqueue2.size();
	n3 = Bigqueue3.size();
	n4 = Bigqueue4.size();
	cout << n1 << " " << n2 << " " << n3 << " " << n4 << endl;

	for(int i = 0; i < n1; i++){
		cout << i << endl;
		A1 = Bigqueue1.front();
		Bigqueue1.pop();
		for(int f = 0; f < n2; f++){
			A2 = Bigqueue2.front();
			Bigqueue2.pop();
			for(int g = 0; g < n3; g++){
				A3 = Bigqueue3.front();
				Bigqueue3.pop();
				for(int h = 0; h < n4; h++){
					A4 = Bigqueue4.front();
					Bigqueue4.pop();
					
					int num = sizeof(total_A) / 4;
					totalA.a[0] = A1;
					totalA.a[1] = A2;
					totalA.a[2] = A3;
					totalA.a[3] = A4;
					for(int i = 0; i < 4; i++){
						fill(totalA.a[i].a, a[4], i);
					}
					
					int ret = initial(a[4], b, c);

					int x = judge(a[4], c);
					if(x == 1){
						backTrack(a[4], b, c, 0, 4);
					}

					Bigqueue4.push(A4);
				}
				Bigqueue3.push(A3);
			}
			Bigqueue2.push(A2);
		}
	}
	return 0;
}

Topics: C Algorithm data structure

Programmer Think

Solving combined Sudoku by backtracking method

Solving combined Sudoku by backtracking method

1. Problem description

2. Ideas and Implementation

2.1 single Sudoku solution

2.1.1 storage of Sudoku

2.1.2 calculation of intermediate value

2.1.2.1 calculation of intermediate value of Jiugong grid

2.1.2.2 calculation of row and column intermediate values

2.1.2.3 initializing intermediate values

2.1.2.4 update and restore intermediate values

2.1.3 single Sudoku solving algorithm

2.1.3.1 define data structure

2.1.3.2 backtracking solution

2.2 solving the last Sudoku by combination

2.2.1 Sudoku in the middle

2.2.2 judging the legitimacy of combined Sudoku

2.2.3 combined solution algorithm

3. Experimental results

3.1 results of the first question

3.2 results of the second question

4. Complete code

Hot Topics