preface:
Looking at the paper, I always see integer programming, 0-1 integer programming and mixed integer programming, so I studied it, including problem definition, fast solving tools, etc.
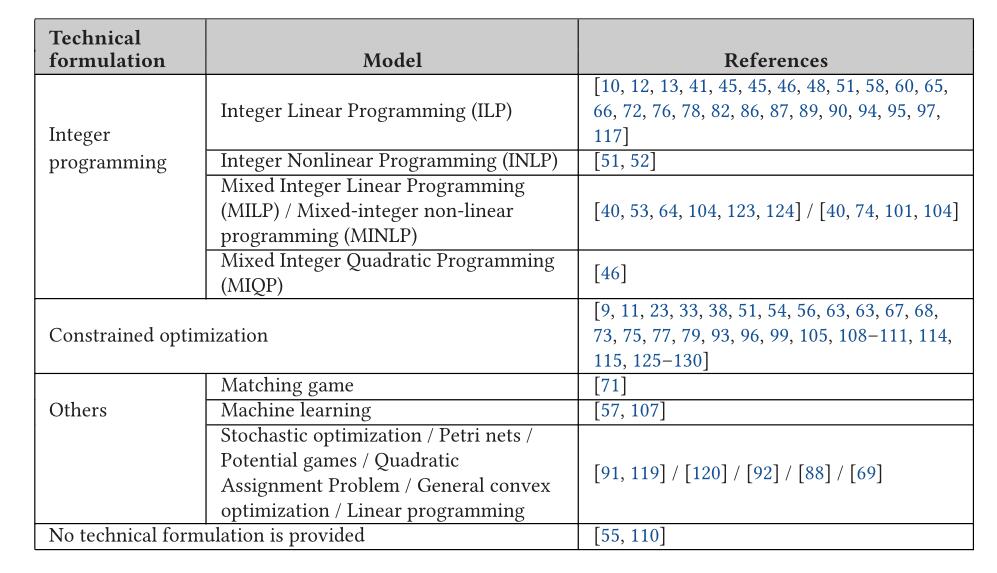
Fir number solver
The fir number solver COPT(Cardinal Optimizer) is an efficient mathematical programming solver suite for large-scale optimization problems independently developed by FIR number. It is also the core component supporting the end-to-end supply chain platform of fir number. It is the only comprehensive mathematical programming solver in China that has the ability to solve large-scale linear programming (simplex method and interior point method) and mixed integer programming problems at the same time, It provides more choices for enterprises to meet the needs of high-performance solutions [1].

How to get
It can be seen from the Shanshu solver online that the solver is currently open to license application and download, especially for academic users, with one-year free trial authority, and 60 days of free trial authority for non academic users. You need to fill in the following application form to apply for it.
I applied the first day and received an email the next day. It can be said that it was quite fast. The email contains the installation package download address, software key and necessary instructions of the solver.
Installation and introduction
The installation is very simple, mainly to configure the software key.
After the software is installed, the contents of the folder under the root path of the installation are shown in the figure:
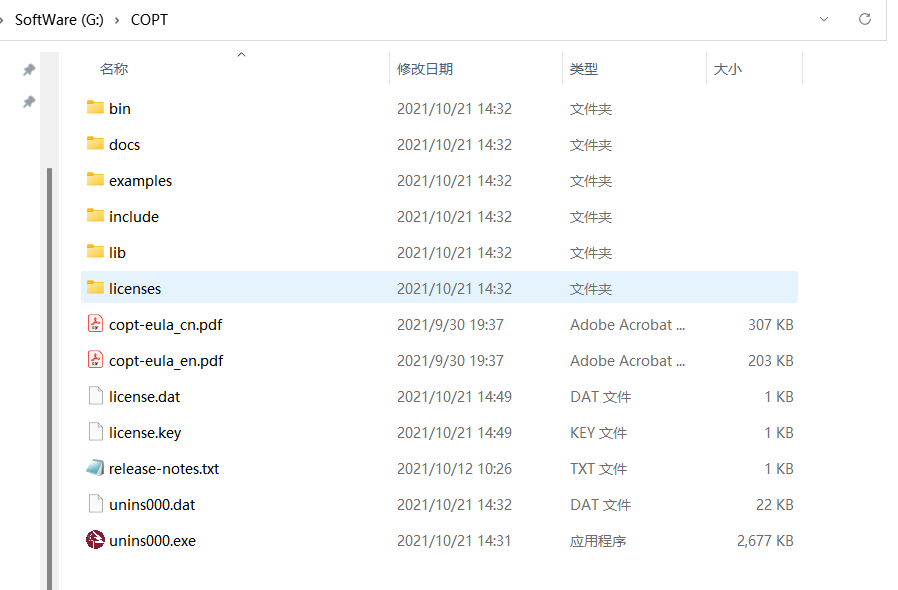
- bin: various dynamic libraries and executable files
- doc: user operation document
- example: programming interface call case
- lib: call the dependent files through the programming interface
Call through JAVA
-
Import jar package
There is copt.jar in the lib folder of the software installation. Copy a copy to the project and add it to the Library.
Take the integrated environment IDEA as an example: copy it to the lib folder of the project (self created) - > right click the lib folder - > Add as library.
-
Programming use
Then you can use the functions of the solver through java programming.
give an example
Solve the problem:
max
z
=
5
x
1
+
8
x
2
s. t.
x
1
+
x
2
≤
6
(
P
0
)
5
x
1
+
9
x
2
≤
45
x
i
≥
0
,
x
i
∈
Z
i
=
1
,
2
\begin{gathered} \max z=5 x_{1}+8 x_{2}\\ \text { s. t. } \quad x_{1}+x_{2} \leq 6\left(P_{0}\right) \\ 5 x_{1}+9 x_{2} \leq 45 \\ x_{i} \geq 0, x_{i} \in \mathbb{Z} \quad i=1,2 \end{gathered}
maxz=5x1+8x2 s. t. x1+x2≤6(P0)5x1+9x2≤45xi≥0,xi∈Zi=1,2
code:
public static void main(String[] args) {
try {
Envr env = new Envr();
Model model = env.createModel("myModel");
// Add variables
// obj: 5x + 8y
// var:
// 0 <= x, y
Var x = model.addVar(0, copt.Consts.INFINITY, 5.0, Consts.INTEGER, "x");
Var y = model.addVar(0, copt.Consts.INFINITY, 8.0, Consts.INTEGER, "y");
// 1. Add linear constraint
// r0: x + y <= 6
// r1: 5x + 9y <= 45
Expr e0 = new Expr(x, 1.0);
e0.addTerm(y, 1.0);
model.addConstr(e0, copt.Consts.LESS_EQUAL, 6.0, "r0");
Expr e1 = new Expr(x,5.0);
e1.addTerm(y,9.0);
model.addConstr(e1, Consts.LESS_EQUAL, 45.0, "r1");
// Set the parameters and properties of the model
model.setDblParam(copt.DblParam.TimeLimit, 10);
model.setObjSense(copt.Consts.MAXIMIZE);
// Solve problem
model.solve();
// Output solution
System.out.println("\nFound optimal solution:");
VarArray vars = model.getVars();
for (int i = 0; i < vars.size(); i++) {
Var var = vars.getVar(i);
System.out.println(" " + var.getName() + " = " + var.get(copt.DblInfo.Value));
}
System.out.println("Obj = " + model.getDblAttr(copt.DblAttr.BestObj));
System.out.println("\nDone");
} catch (CoptException e) {
e.printStackTrace();
}
}
Output:
Cardinal Optimizer v3.0.1. Build date Oct 12 2021
Copyright Cardinal Operations 2021. All Rights Reserved
Setting parameter 'TimeLimit' to 10
Maximizing a MIP problem
The original problem has:
2 rows, 2 columns and 4 non-zero elements
2 integers
Presolving the problem
The presolved problem has:
2 rows, 2 columns and 4 non-zero elements
2 integers
Starting the MIP solver with 8 threads and 16 tasks
Nodes Active LPit/n IntInf BestBound BestSolution Gap Time
0 1 -- 0 1.000000e+30 -- Inf 0.12s
H 0 1 -- 0 1.000000e+30 0.000000e+00 Inf 0.13s
H 0 1 -- 0 1.000000e+30 1.300000e+01 Inf 0.13s
0 1 -- 2 4.125000e+01 1.300000e+01 68.5% 0.14s
H 0 1 -- 2 4.125000e+01 3.400000e+01 17.6% 0.14s
H 0 1 -- 2 4.125000e+01 3.900000e+01 5.45% 0.14s
0 1 -- 2 4.050000e+01 3.900000e+01 3.70% 0.14s
* 0 1 -- 0 4.000000e+01 4.000000e+01 0.00% 0.14s
0 1 -- 0 4.000000e+01 4.000000e+01 0.00% 0.14s
1 0 -- 0 4.000000e+01 4.000000e+01 0.00% 0.14s
Best solution : 40.000000000
Best bound : 40.000000000
Best gap : 0.0000%
Solve time : 0.14
Solve node : 1
MIP status : solved
Solution status : integer optimal (relative gap limit 0.0001)
Violations : absolute relative
bounds : 0 0
rows : 0 0
integrality : 0
Found optimal solution:
x = 0.0
y = 5.0
Obj = 40.0
Done