Problem description

Considering the network transmitting data from the source node to the end node, we first introduce some definitions:
∙ \bullet ∙ K\quad flows: transfer different data in K.
∙ \bullet ∙ L\quad link: l undirected edges connecting network nodes.
∙ \bullet ∙ c l c_l cl: on page l l l the maximum capacity of data transmitted on one edge.
∙ \bullet ∙ P k P_k Pk: the number of alternative path s for different K flows.
∙ \bullet ∙ x k = ( x k , 1 , ... , x k , P K ) T \mathbf{x_k}=\left(x_{k,1}, \ldots, x_{k,P_{K}}\right)^T xk​=(xk,1​,...,xk,PK​​)T: x k , i x_{k,i} xk,i = for k\quad flow, in the i i i is the amount of data allocated by one side of the road.
Given directional quantity C = ( c 1 , c 2 , ... , c L ) T C=\left(c_{1}, c_{2}, \ldots, c_{L}\right)^T C=(c1, c2,..., cL) T, where c l ∈ R + , ∀ l c_l \in R^{+},\forall{l} cl​∈R+,∀l. definition:
R k = ( R 1 , 1 k R 1 , 2 k ⋯ R 1 , P k k R 2 , 1 k R 2 , 2 k ⋯ R 2 , P k k ⋮ ⋮ ⋱ ⋮ R L , 1 k R L , 2 k ⋯ R L , P k k ) R_{k}=\left(\begin{array}{cccc} R_{1,1}^{k} & R_{1,2}^{k} & \cdots & R_{1, P_{k}}^{k} \\ R_{2,1}^{k} & R_{2,2}^{k} & \cdots & R_{2, P_{k}}^{k} \\ \vdots & \vdots & \ddots & \vdots \\ R_{L, 1}^{k} & R_{L, 2}^{k} & \cdots & R_{L, P_{k}}^{k} \end{array}\right) Rk​=⎝⎜⎜⎜⎛​R1,1k​R2,1k​⋮RL,1k​​R1,2k​R2,2k​⋮RL,2k​​⋯⋯⋱⋯​R1,Pk​k​R2,Pk​k​⋮RL,Pk​k​​⎠⎟⎟⎟⎞​
among R k R_{k} Any element in Rk + ∈ { 0 , 1 } \in \{0,1\} ∈{0,1}， P = ∑ i = 1 K P i P=\sum_{i=1}^{K}P_i P = ∑ i=1K ∑ Pi, definition R ∈ R L × P R \in R^{L\times P} R∈RL × P. Among them R l , i k = 1 R_{l,i}^k = 1 Rl,ik = 1 indicates that when k\quad flow is transported, the second i i Road i will pass through No l l l edge:
R = ( R 1 , ... , R K ) R=\left(R_{1}, \ldots, R_{K}\right) R=(R1​,...,RK​)
Define vector x k = ( x k , 1 , x k , 2 , ... , x k , P k ) T x_k=\left(x_{k,1}, x_{k,2}, \ldots, x_{k,P_{k}}\right)^T xk = (xk,1, xk,2,..., xk,Pk) T, where x k , i ≥ 0 , ∀ k , i x_{k,i} \geq 0,\forall{k,i} xk,i ≥ 0, ∀ k,i, and x k , P k > 0 , ∀ k x_{k,P_{k}} > 0,\forall{k} xk,Pk​​>0,∀k. definition x = ( x 1 , ... , x k ) ∈ R P x = (x_1,\ldots,x_k)\in R^P x=(x1​,…,xk​)∈RP. With these definitions, the description of Problem 1 is given:
min ⁡ X max ⁡ l R [ l ] x c l \min _{X} \max _{l} \frac{R[l] x}{c_{l}} minX​maxl​cl​R[l]x​
 s.t.  R x ≤ C ∥ x k ∥ 1 = d k x ≥ 0 \text { s.t. } Rx \leq C \\{ } \left\|x_{k}\right\|_{1}=d_{k} \\ x \geq 0  s.t. Rx≤C∥xk​∥1​=dk​x≥0
It is transformed into standard linear programming problem
Introducing intermediate variables t = max ⁡ l y l c l t = \max_{l}\frac{y_l}{c_l} t=maxl cl yl, it can be written in the following form:
min ⁡ t , x , α , β t \min _{t,x,\alpha,\beta} t mint,x,α,β​t
 s.t.  R x + α = C , R x + β = t C , 1 T x k = d k , x ≥ 0 , α ≥ 0 , β ≥ 0 , t ≥ 0. \text { s.t. } Rx + \alpha = C,\\{ } Rx + \beta = tC, \\{ } \boldsymbol{1}^T x_k = d_k,\\ x \geq 0,\alpha \geq 0,\beta \geq 0,t \geq 0.  s.t. Rx+α=C,Rx+β=tC,1Txk​=dk​,x≥0,α≥0,β≥0,t≥0.
Further modifications were obtained ⟶ \longrightarrow ⟶:
min ⁡ t , x , α , β t , \min _{t,x,\alpha,\beta} t, mint,x,α,β​t,
 s.t.  R x + α = C , t C + α − β = C , 1 T x k = d k , x ≥ 0 , α ≥ 0 , β ≥ 0 , t ≥ 0. \text { s.t. } Rx + \alpha = C,\\{ } tC + \alpha - \beta = C, \\{ } \boldsymbol{1}^T x_k = d_k,\\ x \geq 0,\alpha \geq 0,\beta \geq 0,t \geq 0.  s.t. Rx+α=C,tC+α−β=C,1Txk​=dk​,x≥0,α≥0,β≥0,t≥0.
In this way, we introduce the definition:\
∙ \bullet ∙ c ^ = ( 0 , ... , 0 , 1 ) \hat{c} = (0,\ldots,0,1) c^=(0,...,0,1)\
∙ \bullet ∙ x ^ = ( x , α , β , t ) T \hat{x} = (x,\alpha,\beta,t)^T x^=(x,α,β,t)T\
∙ \bullet ∙ b = ( c 1 , ... , c l , c L , ... , c L , d 1 , ... , d K ) T b = (c_1,\ldots,c_l,c_L,\ldots,c_L,d_1,\ldots,d_K)^T b=(c1​,...,cl​,cL​,...,cL​,d1​,...,dK​)T\
The final standard linear programming problem is obtained:
min ⁡ x ^ c ^ T x ^ , \min _{\hat{x}} \hat{c}^T\hat{x}, minx^​c^Tx^,
 s.t.  A x ^ = b , x ^ ≥ 0. \text { s.t. } A \hat{x} = b,\\{ } \hat{x} \geq 0.  s.t. Ax^=b,x^≥0.
Where defined I L I_L IL ＾ is L L L-order identity matrix, C = ( c 1 , ... , c L ) T C = (c_1,\ldots,c_L)^T C=(c1,..., cL) T and S ∈ R K × P S\in R^{K\times P} S∈RK × P. Matrix S S The first line of S has only the first row P 1 P_1 P1} elements are 1, the rest are 0, and the elements in the second line are only 1 P 1 + 1 , ... , P 1 + P 2 P_1 + 1,\ldots,P_1 + P_2 P1 + 1,..., P1 + P2 is 1 and the rest is 0. Similarly, the last line is only followed P K P_K PK elements are 1 and the rest are 0 The following coefficient matrix is obtained A A Expression of A:
A = [ R I L 0 0 0 I L − I L C S 0 0 0 ] A=\left[\begin{array}{cccc} R & I_L & 0 & 0 \\ 0 & I_L & -I_L & C \\ S & 0 & 0 & 0 \end{array}\right] A=⎣⎡​R0S​IL​IL​0​0−IL​0​0C0​⎦⎤​

Standard linear programming

Consider the standard linear programming problem, where A ∈ R m × n , C ∈ R n , b ∈ R m A \in R^{m \times n},C \in R^{n},b \in R^{m} A∈Rm×n,C∈Rn,b∈Rm:
min ⁡ x C T x \min_{x} C^{T}x minx​CTx
 s.t.  A x = b , \text { s.t. } Ax = b,  s.t. Ax=b,
x ≥ 0. x \geq 0. x≥0.
As we all know, when using simplex method to solve linear programming, we should start from the current pole x x x to the next pole x + x^{+} In the iteration of x +, suppose x x The base index of x is B B B. The non base index is N N N. We have
c T x + = c T x + ( C N − N T B − T C B ) T x N + c^Tx^{+}=c^Tx + (C_N - N^{T}B^{-T}C_B)^Tx_{N}^{+} cTx+=cTx+(CN​−NTB−TCB​)TxN+​
Because in the index N N N, according to the simplex method, x + x^{+} x + only one element greater than 0 is recorded as x q + x_{q}^{+} xq +, if
( C N − N T B − T C B ) T x N + < 0 (C_N - N^{T}B^{-T}C_B)^Tx_{N}^{+} < 0 (CN​−NTB−TCB​)TxN+​<0
be x x x is not the best, and then according to
x B + = B − 1 b − B − 1 A q x q + x_{B}^{+}=B^{-1}b-B^{-1}A_qx_{q}^{+} xB+​=B−1b−B−1Aq​xq+​
We need to choose the right one x q + x_{q}^{+} xq +, which leads to the following criteria.
Dantzig criterion
q = a r g m i n j ∈ N ( C N − N T B − T C B ) j , ( C N − N T B − T C B ) j < 0. q = arg min_{j \in N}(C_N - N^{T}B^{-T}C_B)_j,(C_N - N^{T}B^{-T}C_B)_j < 0. q=argminj∈N​(CN​−NTB−TCB​)j​,(CN​−NTB−TCB​)j​<0.
For this Dantzig criterion, we only select the specific index locations that need to be modified q q q. But specific x q + x_{q}^{+} The value of xq + needs to be determined according to the. The specific method is to choose as large as possible x q + x_{q}^{+} xq +, so that x B + x_{B}^{+} xB + only one element is 0, and other elements are greater than or equal to 0.
Steelest edge guidelines
q = a r g m i n j ∈ N ( C N − N T B − T C B ) j B − 1 N j , ( C N − N T B − T C B ) j < 0. q =arg min_{j \in N}\frac{(C_N - N^{T}B^{-T}C_B)_j}{B^{-1}N_j},(C_N - N^{T}B^{-T}C_B)_j < 0. q=argminj∈N​B−1Nj​(CN​−NTB−TCB​)j​​,(CN​−NTB−TCB​)j​<0.
It can be understood that the Dantzig criterion above is similar to the steepest descent method. The optimal direction of the current iteration is selected for each iteration, but it is not optimal as a whole. This steelest edge criterion is somewhat similar to a normalization.

Solving the initial basic feasible solution by large M method

When solving linear programming problems, we first need an initial point to meet the constraints, and then start from the initial point to iterate the simplex method. After investigation, the large M method and the two-stage method are common. Next, we focus on the process of finding the initial basic feasible solution by the large M method
We consider the standard linear programming problem and introduce a sufficiently large constant M, which is defined C ^ = ( c 1 , ... , c n , M , ... , M ) , A ^ = ( A , I m ) , x ^ = ( x , x n + 1 , ... , x n + m ) \hat{C} = (c_1,\ldots,c_n,M,\ldots,M),\hat{A} = (A,I_{m}),\hat{x} = (x,x_{n + 1},\ldots,x_{n + m}) C^=(c1,..., cn, M,..., M),A^=(A,Im), x^=(x,xn+1,..., xn+m). Now consider the problem:
min ⁡ X C ^ T x ^ \min _{X} \hat{C}^{T}\hat{x} minX​C^Tx^
 s.t.  A ^ x ^ = b , \text { s.t. } \hat{A}\hat{x} = b,  s.t. A^x^=b,
x ^ ≥ 0. \hat{x} \geq 0. x^≥0.
Then, for the linear programming problem, we have the first initial feasible point x ^ = ( 0 , ... , 0 , b 1 , ... , b m ) \hat{x}=(0,\ldots,0,b1,\ldots,b_m) x^=(0,..., 0,b1,..., bm). With this initial feasible point, we can iterate according to the simplex method and get a form of ( x 1 , ... , x n , 0 , ... , 0 ) (x_1,\ldots,x_n,0,\ldots,0) The solution of (x1,..., xn, 0,..., 0) finally obtains the initial feasible point of an original problem ( x 1 , ... , x n ) (x_1,\ldots,x_n) (x1​,...,xn​).
Note: this method is limited to constraint items b ≥ 0 b \geq 0 In the case of b ≥ 0 (so as to ensure that the large M method is correct in the first step), here we need to select m as a sufficiently large constant, so as to ensure that if the original problem has a feasible point, the optimal solution of the new problem must be similar to ( x 1 , ... , x n , 0 , ... , 0 ) (x_1,\ldots,x_n,0,\ldots,0) In the form of (x1,..., xn, 0,..., 0), in our specific operation process, the selection of this M is not fixed. I have done several experiments and found that if Gaussian distribution generation is adopted A , b , c A,b,c A. B, C, because the random seeds are different, sometimes the selection of M will exceed 1 0 20 10^{20} 1020, but in our project, A , b , c A,b,c A. The elements of B and C are relatively small, so they will not be affected.
General linear programming large M method code to solve the initial feasible solution

import numpy as np
import time
import matplotlib.pyplot as plt
def Bland(s,indn):
    ind = np.where(s[:,0]<0)[0]
    q = ind[0]
    return indn[q], q

def DanzigSelect(s,indn):#indn non base index
    q = s.argmin()
    return indn[q], q

def SteepSelect(A_n,s,indn):
    ratio = s/A_n.transpose()
    q = ratio.argmin()
    return indn[q], q
def bigM(c,A,b,piv,M):#The large M method is used to solve the initial basic feasible solution
    eps = 1e-6
    [m,n] = A.shape
    x = np.zeros([n + m,1]);x[n:,:] = b
    
    Ah = np.hstack([A,np.identity(m)])
    ch =  np.vstack([c,M*np.ones([m,1])])
    indb = np.arange(m + n)[n:]#Initial base index
    index = np.arange(0,m + n)
    indn = np.delete(index,indb)
    B = Ah[:,indb]#The initial B is the identity matrix
    B_inv = B
    #print(B)
    N = Ah[:,indn]
    iteration = 0        # determine the max iteration
    
    while iteration < 500:
        y = np.dot(B_inv.T, ch[indb,:])
        s = ch[indn,:] - N.T@y#C_N - N^TB^{-T}C_B
        if all(s >= 0):#It shows that this is the optimal solution
            print('unbelievabel,the resid:%.2e, done,the epoch:%d'%(np.linalg.norm(Ah@x - b),iteration))
            break
        if piv == 'Danzig':
            q1, q2 = DanzigSelect(s, indn)
        if piv == 'steepest-edge':
            A_re = B_inv@N
            A_n = np.linalg.norm(A_re,axis = 0,keepdims = True)
            q1, q2 = SteepSelect(A_n, s, indn)
        if piv == 'Bland':
            q1, q2 = Bland(s, indn)
        #q1 is the index that needs to be replaced in the non base index
        u = B_inv@Ah[:, q1:(q1+1)]   
        if all(u <= 0):#The optimal value is unbounded
            print('Linear program is unbounded.')
            break
            
        inds1 = np.where(u[:,0] > 0)[0]#Find all indexes greater than 0
        inds2 = indb[inds1]#Find all indexes corresponding to greater than 0 in the base index
        ratio = x[inds2,:]/u[inds1,:]
        x_q = min(ratio)        # a number
        p1 = inds2[ratio.argmin()]
        p2 = inds1[ratio.argmin()]
        
        x[indb,:] = x[indb,:]- x_q*u
        vec = np.zeros([indn.size,1])
        vec[q2,0] = x_q
        x[indn,:] = x[indn,:] + vec
        rho = (x[n:,:]**2).mean()
        if iteration%50 == 0:
            
            print('epoch:%d,enter basis:%d,quit basis:%d,resid:%.2e,rest err:%.2e'
                  %(iteration,q1,p1,np.linalg.norm(Ah@x - b),rho))
        
        if rho < eps:
            print('the end epoch:%d,rho:%.2e,the real resid:%.2e'
                  %(iteration,rho,np.linalg.norm(A@x[:n,:] - b)))
            break
        else:
            indb = np.delete(indb,p2)
            indb = np.append(indb,q1)
            indn = np.delete(indn,q2)
            indn = np.append(indn,p1)
            
            B = Ah[:, indb]
            B_inv = np.linalg.inv(B)
            N = Ah[:, indn]
            iteration = iteration + 1
    return x[:n,:]

def simplex(c,A,b,piv,M):
    eps = 1e-6
    [m,n] = A.shape
    x = bigM(c,A,b,piv,M)
    #print(x.shape,A.shape,b.shape,indb.size,m)
    if np.linalg.norm(A@x - b) > eps or (any(x < 0) and min(x) < -eps):
        print('the init solution error')
        return 0
    else:
        print('the init solution come on')
    indb = []
    geq = np.where(x > 0)[0]
    eq = np.where(x <= 0)[0]
    indb = np.append(indb,geq)
    if indb.size == m:
        pass
    elif indb.size < m:
        er = m - indb.size
        print('basic need:%d'%(er))
        ra = np.random.choice(eq,er,replace = False)
        indb = np.append(indb,ra)
    else:
        print('wrong')
        return 0
    index = np.arange(0,n)
    indb = indb.astype('int32')
    indn = np.delete(index,indb)
    B = A[:,indb]
    
    B_inv = np.linalg.inv(B)
    
    N = A[:,indn]
    iteration = 0        # determine the max iteration
    
    while iteration < 2000:
        y = np.dot(B_inv.T, c[indb,:])
        s = c[indn,:] - N.T@y#C_N - N^TB^{-T}C_B
        value = (c*x).sum()
        if all(s >= 0) or (any(s < 0) and min(s) > -eps):#It shows that this is the optimal solution
            print('the end epoch:%d,resid:%.2e,opt val:%.2e'
                  %(iteration,np.linalg.norm(A@x - b),value))
            break
        if piv == 'Danzig':
            q1, q2 = DanzigSelect(s, indn)
        if piv == 'steepest-edge':
            A_re = B_inv@N
            A_n = np.linalg.norm(A_re,axis = 0,keepdims = True)
            q1, q2 = SteepSelect(A_n, s, indn)
        if piv == 'Bland':
            q1, q2 = Bland(s, indn)
        #q1 is the index that needs to be replaced in the non base index
        u = B_inv@A[:, q1:(q1+1)]   
        if all(u <= 0):#The optimal value is unbounded
            print('Linear program is unbounded.')
            break
            
        inds1 = np.where(u[:,0] > 0)[0]#Find all indexes greater than 0
        inds2 = indb[inds1]#Find all indexes corresponding to greater than 0 in the base index
        ratio = x[inds2,:]/u[inds1,:]
        x_q = min(ratio)        # a number
        p1 = inds2[ratio.argmin()]
        p2 = inds1[ratio.argmin()]
        
        x[indb,:] = x[indb,:]- x_q*u
        vec = np.zeros([indn.size,1])
        vec[q2,0] = x_q
        x[indn,:] = x[indn,:] + vec
        res = np.linalg.norm(A@x - b)
        if res > eps:
            print('blow up,epoch:%d,resid:%.2e'%(iteration,res))
            break
        if iteration%100 == 0:
            #print(np.linalg.det(B))
            print('epoch:%d,enter basis:%d,quit basis:%d,resid:%.2e,opt val:%.2e'
                  %(iteration,q1,p1,res,value))
        indb = np.delete(indb,p2)
        indb = np.append(indb,q1)
            
        indn = np.delete(indn,q2)
        indn = np.append(indn,p1)
            
        B = A[:, indb]
        B_inv = invB(B_inv,p2,u)
           
        N = A[:, indn]
        iteration = iteration + 1
    return x

L1 = 100
P1 = 200
k = 5
p = 0.02

np.random.seed(1234)

R = np.random.binomial(1,p,[L1,P1])#Binomial distribution, generate [L1,P1] row array, all elements are 0 or 1
d = np.random.gamma(2,2,[k,1])*1#gamma distribution,
u = np.random.gamma(2,2,[L1,1])*3+20
s = P1 - k
ind = np.random.randint(0,k,s)#Randomly extract an integer between 0 and K
S = np.zeros((k,s))
for i in range(s):
    j = ind[i]
    S[j,i] = 1
S = np.hstack((np.identity(k),S))

n = P1+2*L1+1       #364
m = 2*L1+k          #196

# construct the vector c, only the last element is 1
c = np.zeros((n,1))
c[-1,0] = 1

print(c.shape, c[-1,0])

# construct the matrix A
S1 = np.hstack((R,np.zeros((L1,L1)),np.identity(L1),np.zeros((L1,1))))
S2 = np.hstack((np.zeros((L1,P1)),-np.identity(L1),np.identity(L1),u))
S3 = np.hstack((S,np.zeros((k,(2*L1+1)))))
A = np.vstack((S1,S2,S3))

b = np.vstack((u,u,d))
piv = 'Bland'

M = 1e6
x = bigM(c,A,b,piv,M)
#x = simplex(c,A,b,piv,M)

Solving the initial feasible solution by two-stage method

Briefly introduce the two-stage method. Compared with the big M method mentioned above, the biggest advantage of the two-stage method is that it does not need to select the super parameter M. Still taking the standard linear programming problem as an example, our solution process is divided into two stages. Consider the first phase below, where y = ( y 1 , ... , y m ) y = (y_1,\ldots,y_m) y=(y1​,...,ym​):
min ⁡ x , y ∑ i = 1 m y i \min_{x,y} \sum_{i = 1}^m y_i minx,y​∑i=1m​yi​
 s.t.  A x + I m y = b , \text { s.t. } Ax + I_m y = b,  s.t. Ax+Im​y=b,
x , y ≥ 0. x,y \geq 0. x,y≥0.
Solving linear programming, if the optimal value is not 0, it shows that the original linear programming has no feasible solution. If the optimal value is 0, we need to consider the following cases:
The first case: the optimal solution of the problem ( x , y ) (x,y) The base index of (x,y) contains artificial variables y y The index of y indicates that the original linear programming is degraded. At this time, some replacement needs to be made to continuously include y y The base index of y is replaced, and then the initial feasible solution is obtained.
The second case: the optimal solution of the problem ( x , y ) (x,y) The base index of (x,y) does not contain artificial variables y y y, which means that we can directly x x x is used as an initial feasible solution.
It is very simple to carry out the second stage on the basis of the first stage, which can be iterated by the simplex method directly according to the initial feasible solution.
General linear programming two-stage method code

import numpy as np

def Bland(s,indn):
    ind = np.where(s[:,0]<0)[0]
    q = ind[0]
    return indn[q], q

def DanzigSelect(s,indn):#indn non base index
    q = s.argmin()
    return indn[q], q

def SteepSelect(A_n,s,indn):
    ratio = s/A_n.transpose()
    q = ratio.argmin()
    return indn[q], q
def invB(B_inv,p,u):
    Bv = B_inv.copy()
    Bv[p,:] = Bv[p,:]/u[p,0]
    m = u.size
    ind = []
    for i in range(m):
        if i == p:
            pass
        else:
            ind.append(i)
            Bv[i,:] = Bv[i,:] - u[i,0]*Bv[p,:]
    ind.append(p)
    Bv = Bv[ind,:]
    return Bv
def stage_one(A,b,piv):#The large M method is used to solve the initial basic feasible solution
    eps = 1e-6
    [m,n] = A.shape
    x = np.zeros([n + m,1]);x[n:,:] = b
    
    Ah = np.hstack([A,np.identity(m)])
    ch =  np.zeros([n + m,1]);ch[n:,:] = np.ones([m,1])
    indb = np.arange(m + n)[n:]#Initial base index
    index = np.arange(0,m + n)
    indn = np.delete(index,indb)
    B = Ah[:,indb]#The initial B is the identity matrix
    B_inv = B
    
    N = Ah[:,indn]
    iteration = 0        # determine the max iteration
    
    while iteration < 1000:
        
        y = np.dot(B_inv.T, ch[indb,:])
        s = ch[indn,:] - N.T@y#C_N - N^TB^{-T}C_B
        if all(s >= 0):#It shows that this is the optimal solution
            print('unbelievabel,the resid:%.2e, done,the epoch:%d'%(np.linalg.norm(Ah@x - b),iteration))
            break
        if piv == 'Danzig':
            q1, q2 = DanzigSelect(s, indn)
        if piv == 'steepest-edge':
            A_re = B_inv@N
            A_n = np.linalg.norm(A_re,axis = 0,keepdims = True)
            q1, q2 = SteepSelect(A_n, s, indn)
        if piv == 'Bland':
            q1, q2 = Bland(s, indn)
        #q1 is the index that needs to be replaced in the non base index
        u = B_inv@Ah[:, q1:(q1+1)]   
        if all(u <= 0):#It shows that the optimal value is unbounded
            print('Linear program is unbounded.')
            break
            
        inds1 = np.where(u[:,0] > 0)[0]#Find all indexes greater than 0
        inds2 = indb[inds1]#Find all indexes corresponding to greater than 0 in the base index
        ratio = x[inds2,:]/u[inds1,:]
        x_q = min(ratio)        # a number
        p1 = inds2[ratio.argmin()]
        p2 = inds1[ratio.argmin()]
        
        x[indb,:] = x[indb,:]- x_q*u
        vec = np.zeros([indn.size,1])
        vec[q2,0] = x_q
        x[indn,:] = x[indn,:] + vec
        aug = np.linalg.norm(Ah@x - b)
        if aug > eps:
            print('blow up,epoch:%d,aug resid:%.2e'%(iteration,aug))
            break
        value = x[n:,:].sum()
        if iteration%100 == 0:
            
            print('epoch:%d,enter basis:%d,quit basis:%d,resid:%.2e,opt val:%.2e'
                  %(iteration,q1,p1,aug,value))
        
        if value < eps:
            print('the end epoch:%d,opt val:%.2e,the real resid:%.2e'
                  %(iteration,value,np.linalg.norm(A@x[:n,:] - b)))
            break
        else:
            
            indb = np.delete(indb,p2)
            indb = np.append(indb,q1)
            
            indn = np.delete(indn,q2)
            indn = np.append(indn,p1)
            
            B = Ah[:, indb]
            B_inv = invB(B_inv,p2,u)
           
            N = Ah[:, indn]
            iteration = iteration + 1
    return x[:n,:]

def stage_two(c,A,b,piv,L,P,K):
    eps = 1e-6
    [m,n] = A.shape
    x = stage_one(A,b,piv)
    
    if np.linalg.norm(A@x - b) > eps or (any(x < 0) and min(x) < -eps):
        print('the init solution error')
        print('---------------------------------------')
        return 0
    else:
        print('the init solution come on')
        print('---------------------------------------')
    geq = np.where(x > eps)[0]
    eq = np.where(x == 0)[0]
    #eeq = np.where(any(x > 0 and x < eps))[0]
    if geq.size < m:
        er = m - geq.size
        ra = np.random.choice(eq.size,er)
        indb = np.append(geq,eq[ra])
    elif geq.size > m:
        print('error')
        return 0
    else:
        indb = geq
    index = np.arange(0,n)
    indn = np.delete(index,indb)
    B = A[:,indb]
    
    B_inv = np.linalg.inv(B)
    
    N = A[:,indn]
    iteration = 0        # determine the max iteration
    
    while iteration < 2000:
        y = np.dot(B_inv.T, c[indb,:])
        s = c[indn,:] - N.T@y#C_N - N^TB^{-T}C_B
        value = (c*x).sum()
        if all(s >= 0) or (any(s < 0) and min(s) > -eps):#It shows that this is the optimal solution
            print('the end epoch:%d,resid:%.2e,opt val:%.2e'
                  %(iteration,np.linalg.norm(A@x - b),value))
            break
        if piv == 'Danzig':
            q1, q2 = DanzigSelect(s, indn)
        if piv == 'steepest-edge':
            A_re = B_inv@N
            A_n = np.linalg.norm(A_re,axis = 0,keepdims = True)
            q1, q2 = SteepSelect(A_n, s, indn)
        if piv == 'Bland':
            q1, q2 = Bland(s, indn)
        #q1 is the index that needs to be replaced in the non base index
        u = B_inv@A[:, q1:(q1+1)]   
        if all(u <= 0):#The optimal value is unbounded
            print('Linear program is unbounded.')
            break
            
        inds1 = np.where(u[:,0] > 0)[0]#Find all indexes greater than 0
        inds2 = indb[inds1]#Find all indexes corresponding to greater than 0 in the base index
        ratio = x[inds2,:]/u[inds1,:]
        x_q = min(ratio)        # a number
        p1 = inds2[ratio.argmin()]
        p2 = inds1[ratio.argmin()]
        
        x[indb,:] = x[indb,:]- x_q*u
        vec = np.zeros([indn.size,1])
        vec[q2,0] = x_q
        x[indn,:] = x[indn,:] + vec
        res = np.linalg.norm(A@x - b)
        if res > eps:
            print('blow up,epoch:%d,resid:%.2e'%(iteration,res))
            break
        if iteration%100 == 0:
            #print(np.linalg.det(B))
            print('epoch:%d,enter basis:%d,quit basis:%d,resid:%.2e,opt val:%.2e'
                  %(iteration,q1,p1,res,value))
        indb = np.delete(indb,p2)
        indb = np.append(indb,q1)
            
        indn = np.delete(indn,q2)
        indn = np.append(indn,p1)
            
        B = A[:, indb]
        B_inv = invB(B_inv,p2,u)
           
        N = A[:, indn]
        iteration = iteration + 1
    return x


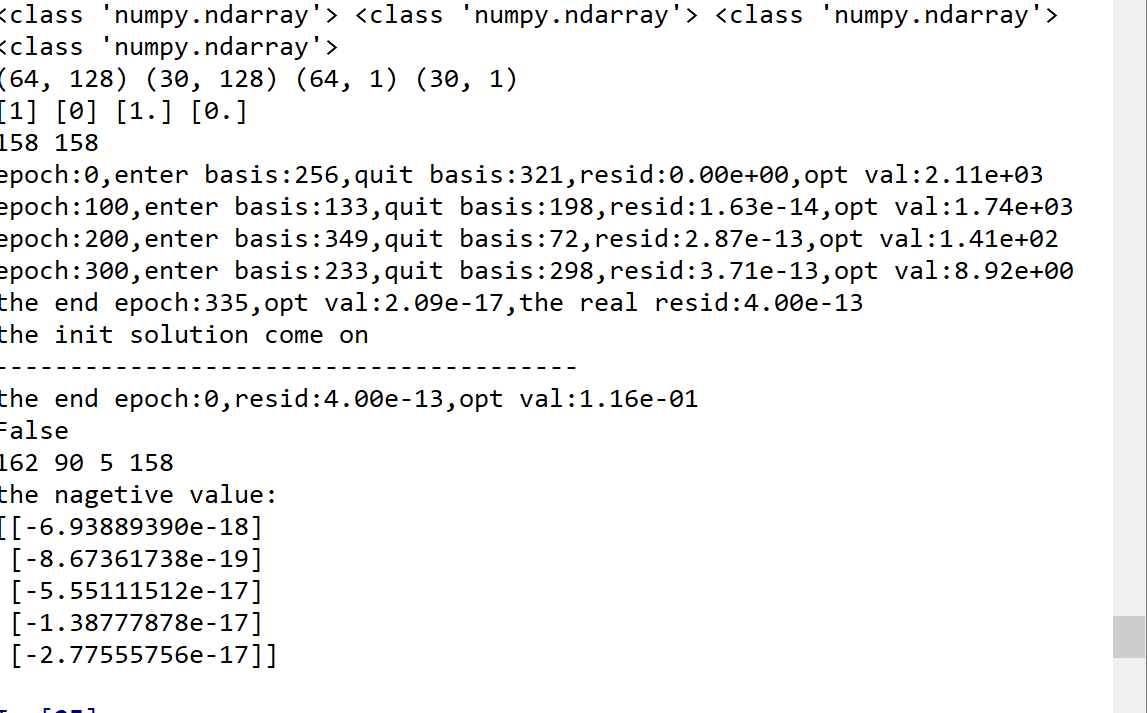
L = 64
P = 128
K = 30
p = 0.02

np.random.seed(1)

# seed 1 with 512,1024, Danzig beats steepest
# seed 1 with 256, 512 steepest beats Danzig

R = np.random.binomial(1,p,[L,P])#Binomial distribution, generate [L1,P1] row array, all elements are 0 or 1
d = np.random.gamma(2,2,[K,1])*1#gamma distribution,
u = np.random.gamma(2,2,[L,1])*3+20
s = P - K
ind = np.random.randint(0,K,s)#Randomly extract an integer between 0 and K
S = np.zeros((K,s))
for i in range(s):
    j = ind[i]
    S[j,i] = 1
S = np.hstack((np.identity(K),S))

#---------------------------------
L = R.shape[0];P = R.shape[1];K = S.shape[0]
m = 2*L + K;n = P + 2*L + 1
print(type(R),type(S),type(u),type(d))
print(R.shape,S.shape,u.shape,d.shape)
print(max(R.reshape(-1,1)),min(R.reshape(-1,1)),max(S.reshape(-1,1)),min(S.reshape(-1,1)))
row1 = np.hstack([R,np.identity(L),np.zeros([L,L]),np.zeros([L,1])])
row2 = np.hstack([np.zeros([L,P]),np.identity(L),-np.identity(L),u])
row3 = np.hstack([S,np.zeros([K,2*L + 1])])
A = np.vstack([row1,row2,row3])
print(np.linalg.matrix_rank(A),m)
b = np.vstack([u,u,d])
c = np.zeros([n,1]);c[-1,0] = 1.0
#piv = 'Bland'
piv = 'Danzig'
x = stage_two(c,A,b,piv,L,P,K)


print(all(x >= 0))
geq = np.where(x > 0)[0]
eq = np.where(x == 0)[0]
leq = np.where(x < 0)[0]
print(geq.size,eq.size,leq.size,m)
print('the nagetive value:')
print(x[leq])
#----------------------

The simplex method is used to solve the above linear programming

Selection of initial feasible solution
After we have introduced some criteria and concepts of simplex method and given the specific form of linear programming to be solved in our project, we will give the specific method of using simplex method to solve our project in this section.
First, we need to obtain the first initial feasible solution to start the simplex method. In practice, we find that if we simply use the large M method or the two-stage method to solve the first initial feasible solution, the algorithm becomes very unstable when the matrix scale is too large, Therefore, we come up with a simplex construction method for such a matrix to construct the first feasible solution. Specifically, the first sub problem is given as follows:
min ⁡ x , y ∑ i = 1 K + L z i ，  s.t.  S x = d , R x + y = C , x ≥ 0. \begin{array}{cl} \min _{x,y} & \sum_{i = 1}^{K + L} z_i， \\ \text { s.t. } & Sx = d,\\{ } & Rx + y = C,\\{ }& x \geq 0. \end{array} minx,y​ s.t. ​∑i=1K+L​zi​，Sx=d,Rx+y=C,x≥0.​
The first stage of the two-stage method is used to solve the first sub problem \ ref{sub1}, which may be recorded as ( x , y ) = ( x 1 : P , x P : P + L ) (x,y)=(x_{1:P},x_{P:P + L}) (x,y)=(x1:P​,xP:P+L​). \
Then we define a variable t t t. Definitions are given later. Now let's define the second sub problem: x P : P + L − x + t C = C x_{P:P+L} - x + tC=C xP:P+L​−x+tC=C
The solution obtained by solving the second subproblem is recorded as x P + L : P + 2 L x_{P+L:P+2L} xP+L:P+2L, which is easy to see x P + L : P + 2 L = x P : P + L + ( t − 1 ) C x_{P+L:P+2L}=x_{P:P+L} + (t-1)C xP+L:P+2L​=xP:P+L​+(t−1)C. Finally, we get the first initial feasible solution as follows:
∙ \bullet ∙ x = ( x 1 : P , x P : P + L , x P + L : P + 2 L , t ) x = (x_{1:P},x_{P:P+L},x_{P+L:P+2L},t) x=(x1:P​,xP:P+L​,xP+L:P+2L​,t)
According to the above solution process, we know x 1 : P ≥ 0 ， x P : P + L ≥ 0 x_{1:P} \geq 0，x_{P:P+L} \geq 0 x1:P ≥ 0, xP:P+L ≥ 0, and the number of elements with 0 is at least P − K P - K P−K. If the number of elements is 0 P − K + 1 P - K + 1 P − K+1, we choose the appropriate t ≥ 0 t \geq 0 If t ≥ 0, there will be x ≥ 0 x \geq 0 x ≥ 0, the number of non-0 elements of the solution obtained at this time is at least P + 1 − K = m − n P + 1 - K = m - n P+1 − K=m − n, then this can be used as our initial feasible solution. \par
If the number of elements with 0 is exactly P − K P - K P − K, we can choose the right one t ≥ 0 t \geq 0 t ≥ 0, select here t = 1 − min ⁡ 0 ≤ j ≤ L − 1 x P : P + j C j t = 1 - \min_{0 \leq j \leq L-1}\frac{x_{P:P+j}}{C_j} t=1 − min0 ≤ j ≤ L − 1 − Cj xP:P+j, which is actually the original problem t = 1 − min ⁡ 0 ≤ j ≤ L − 1 α C j t = 1 - \min_{0 \leq j \leq L-1}\frac{\alpha}{C_j} t=1−min0≤j≤L−1​Cj​ α , because R x + α = C Rx+\alpha=C Rx+ α= C. Obviously t ≥ 0 t \geq 0 t ≥ 0, so that x P + L : P + 2 L x_{P+L:P+2L} xP+L:P+2L ， only one element is 0, and the others are greater than 0. Through this process, the number of non-0 elements of the solution is at least P + 1 − K = n − m P + 1 - K = n - m P+1 − K=n − m, then the initial feasible solution is also obtained
Selection of iterative method
After we get the initial feasible solution, we need to make a judgment if the initial feasible solution x 0 x_0 x0} exists m m If m elements are greater than 0 and the other elements are 0, we can get the corresponding base index. If the initial feasible solution x 0 x_0 x0} the number of elements greater than 0 is less than m m m. Then we need to take out the indexes of those elements greater than 0, and then select the number of difference indexes according to the appropriate principles to get the base index.
In the specific code implementation, we can use the two criteria mentioned above. Here, we need to solve the base matrix B B We also deal with the inverse matrix of B. Given the base matrix used in the last iteration, we record it as B 1 B_1 B1, assumptions B 1 = ( A 1 , ... , A p − 1 , A p , A p + 1 , ... , A m ) B_1 = (A_{1},\ldots,A_{p-1},A_{p},A_{p+1},\ldots,A_{m}) B1 = (A1,..., Ap − 1, Ap, Ap+1,..., Am) and the corresponding inverse matrix B 1 − 1 B_1^{-1} Under the premise of B1 − 1, the new base matrix B 2 = ( A 1 , ... , A p − 1 , A p + 1 , ... , A m , A q ) B_2 = (A_{1},\ldots,A_{p-1},A_{p+1},\ldots,A_{m},A_q) B2 = (A1,..., Ap − 1, Ap+1,..., Am, Aq), then we have B 1 − 1 B 2 = ( e 1 , ... , e p − 1 , e p + 1 , ... , e m , B 1 − 1 A q ) B_1^{-1}B_2 = (e_1,\ldots,e_{p-1},e_{p+1},\ldots,e_m,B_1^{-1}A_q) B1 − 1 − B2 = (e1,..., ep − 1, ep+1,..., em, B1 − 1 − Aq). At this time, we can B 1 − 1 B_1^{-1} A new matrix is obtained by elementary transformation based on B1 − 1 B 2 B_2 The inverse matrix of B2.

Data generation

To facilitate the display of the results, here we show the data generation mode:

The code for solving the above specific linear programming problem
randsimplex.py
Update base index by random selection criteria

import numpy as np
import time
def Bland(s,indn):
    ind = np.where(s[:,0]<0)[0]
    q = ind[0]
    return indn[q], q

def DanzigSelect(s,indn):#indn non base index
    q = s.argmin()
    return indn[q], q

def SteepSelect(A_n,s,indn):
    ratio = s/A_n.transpose()
    q = ratio.argmin()
    return indn[q], q
def invB(B_inv,p,u):
    Bv = B_inv.copy()
    Bv[p,:] = Bv[p,:]/u[p,0]
    m = u.size
    ind = []
    for i in range(m):
        if i == p:
            pass
        else:
            ind.append(i)
            Bv[i,:] = Bv[i,:] - u[i,0]*Bv[p,:]
    ind.append(p)
    Bv = Bv[ind,:]
    return Bv
def stage_one(A,b):#The large M method is used to solve the initial basic feasible solution
    eps = 1e-6
    [m,n] = A.shape
    x = np.zeros([n + m,1]);x[n:,:] = b
    
    Ah = np.hstack([A,np.identity(m)])
    ch =  np.zeros([n + m,1]);ch[n:,:] = np.ones([m,1])
    indb = np.arange(m + n)[n:]#Initial base index
    index = np.arange(0,m + n)
    indn = np.delete(index,indb)
    B = Ah[:,indb]#The initial B is the identity matrix
    B_inv = B
    
    N = Ah[:,indn]
    iteration = 0        # determine the max iteration
    
    while iteration < 1000:
        
        y = np.dot(B_inv.T, ch[indb,:])
        s = ch[indn,:] - N.T@y#C_N - N^TB^{-T}C_B
        if all(s >= 0):#It shows that this is the optimal solution
            print('unbelievabel,the resid:%.2e, done,the epoch:%d'%(np.linalg.norm(Ah@x - b),iteration))
            break
        z = np.random.rand(1)
        if (z >= 0 and z <= 1/3):
            q1, q2 = DanzigSelect(s, indn)
        elif (z >= 1/3 and z <= 2/3):
            A_re = B_inv@N
            A_n = np.linalg.norm(A_re,axis = 0,keepdims = True)
            q1, q2 = SteepSelect(A_n, s, indn)
        else:
            q1, q2 = Bland(s, indn)
        #q1 is the index that needs to be replaced in the non base index
        u = B_inv@Ah[:, q1:(q1+1)]   
        if all(u <= 0):#The optimal value is unbounded
            print('Linear program is unbounded.')
            break
            
        inds1 = np.where(u[:,0] > 0)[0]#Find all indexes greater than 0
        inds2 = indb[inds1]#Find all indexes corresponding to greater than 0 in the base index
        ratio = x[inds2,:]/u[inds1,:]
        x_q = min(ratio)        # a number
        p1 = inds2[ratio.argmin()]
        p2 = inds1[ratio.argmin()]
        
        x[indb,:] = x[indb,:]- x_q*u
        vec = np.zeros([indn.size,1])
        vec[q2,0] = x_q
        x[indn,:] = x[indn,:] + vec
        aug = np.linalg.norm(Ah@x - b)
        if aug > eps:
            print('blow up,epoch:%d,aug resid:%.2e'%(iteration,aug))
            break
        value = x[n:,:].sum()
        if iteration%100 == 0:
            
            print('epoch:%d,enter basis:%d,quit basis:%d,resid:%.2e,opt val:%.2e'
                  %(iteration,q1,p1,aug,value))
        
        if value < eps and all(s) >= 0:
            print('the end epoch:%d,opt val:%.2e,the real resid:%.2e'
                  %(iteration,value,np.linalg.norm(A@x[:n,:] - b)))
            break
        else:
            
            indb = np.delete(indb,p2)
            indb = np.append(indb,q1)
            
            indn = np.delete(indn,q2)
            indn = np.append(indn,p1)
            
            B = Ah[:, indb]
            B_inv = invB(B_inv,p2,u)
           
            N = Ah[:, indn]
            iteration = iteration + 1
    return x[:n]
def MCF(A,b,L,P,K):
    S = A[2*L:,:P]
    R = A[:L,:P]
    indb = []
    [m,n] = A.shape
    u = b[:L,:];d = b[2*L:,:]
    
    A1 = np.hstack([S,np.zeros([K,L])])
    A2 = np.hstack([R,np.identity(L)])
    Ar = np.vstack([A1,A2])
    br = np.vstack([d,u])
    x = np.zeros([n,1])
    x[:P + L,:] = stage_one(Ar,br)
    geq = np.where(x[:P + L,:] > 0)[0]
    indb = np.append(indb,geq)
    #print(indb.size,K + L)
    if geq.size < K + L:
        radio = min(x[P:P + L,:]/u)
        M = 1.0 - radio# + 1e-2
        
        geq3 = np.arange(P + L,P + 2*L)
        indb = np.append(indb,geq3)
        if indb.size == K + 2*L - 1:
            pass
        else:
            er = K + 2*L - 1 - indb.size
            index = np.setdiff1d(np.arange(0,P + L),geq)
            ra = np.random.choice(index,er,replace = False)
            indb = np.append(indb,ra)
    else:
        radio = min(x[P:P + L,:]/u)
        ind = np.argmin(x[P:P + L,:]/u) + P + L
        geq3 = np.setdiff1d(np.arange(P + L,P + 2*L),ind)
        indb = np.append(indb,geq3)
        M = 1 - radio
    x[-1,0] = M
    indb = np.append(indb,P + 2*L)
    for i in range(L):
        x[P + L + i,0] = x[P + i,0] + (M - 1)*u[i,0]
    
    #print(indb.size)
    return x,indb
def stage_two(c,A,b,L,P,K):
    eps = 1e-6
    [m,n] = A.shape
    x,indb = MCF(A,b,L,P,K)
    #print(x.shape,A.shape,b.shape,indb.size,m)
    if np.linalg.norm(A@x - b) > eps or (any(x < 0) and min(x) < -eps):
        print('the init solution error')
        return 0
    else:
        print('the init solution come on')
    
    indb = indb.astype('int32')
    index = np.arange(0,n)
    indn = np.delete(index,indb)
    B = A[:,indb]
    
    B_inv = np.linalg.inv(B)
    
    N = A[:,indn]
    iteration = 0        # determine the max iteration
    
    while iteration < 3000:
        y = np.dot(B_inv.T, c[indb,:])
        s = c[indn,:] - N.T@y#C_N - N^TB^{-T}C_B
        value = (c*x).sum()
        if all(s >= 0) or (any(s < 0) and min(s) > -eps):#It shows that this is the optimal solution
            print('the end epoch:%d,resid:%.2e,opt val:%.2e'
                  %(iteration,np.linalg.norm(A@x - b),value))
            break
        z = np.random.rand(1)
        if (z >= 0 and z <= 1/3):
            q1, q2 = DanzigSelect(s, indn)
        elif (z >= 1/3 and z <= 2/3):
            A_re = B_inv@N
            A_n = np.linalg.norm(A_re,axis = 0,keepdims = True)
            q1, q2 = SteepSelect(A_n, s, indn)
        else:
            q1, q2 = Bland(s, indn)
        
        #q1 is the index that needs to be replaced in the non base index
        u = B_inv@A[:, q1:(q1+1)]   
        if all(u <= 0):#The optimal value is unbounded
            print('Linear program is unbounded.')
            break
            
        inds1 = np.where(u[:,0] > 0)[0]#Find all indexes greater than 0
        inds2 = indb[inds1]#Find all indexes corresponding to greater than 0 in the base index
        ratio = x[inds2,:]/u[inds1,:]
        x_q = min(ratio)        # a number
        p1 = inds2[ratio.argmin()]
        p2 = inds1[ratio.argmin()]
        
        x[indb,:] = x[indb,:]- x_q*u
        vec = np.zeros([indn.size,1])
        vec[q2,0] = x_q
        x[indn,:] = x[indn,:] + vec
        res = np.linalg.norm(A@x - b)
        if res > eps:
            print('blow up,epoch:%d,resid:%.2e'%(iteration,res))
            break
        if iteration%100 == 0:
            #print(np.linalg.det(B))
            print('epoch:%d,enter basis:%d,quit basis:%d,resid:%.2e,opt val:%.2e'
                  %(iteration,q1,p1,res,value))
        indb = np.delete(indb,p2)
        indb = np.append(indb,q1)
            
        indn = np.delete(indn,q2)
        indn = np.append(indn,p1)
            
        B = A[:, indb]
        B_inv = invB(B_inv,p2,u)
           
        N = A[:, indn]
        iteration = iteration + 1
    return x




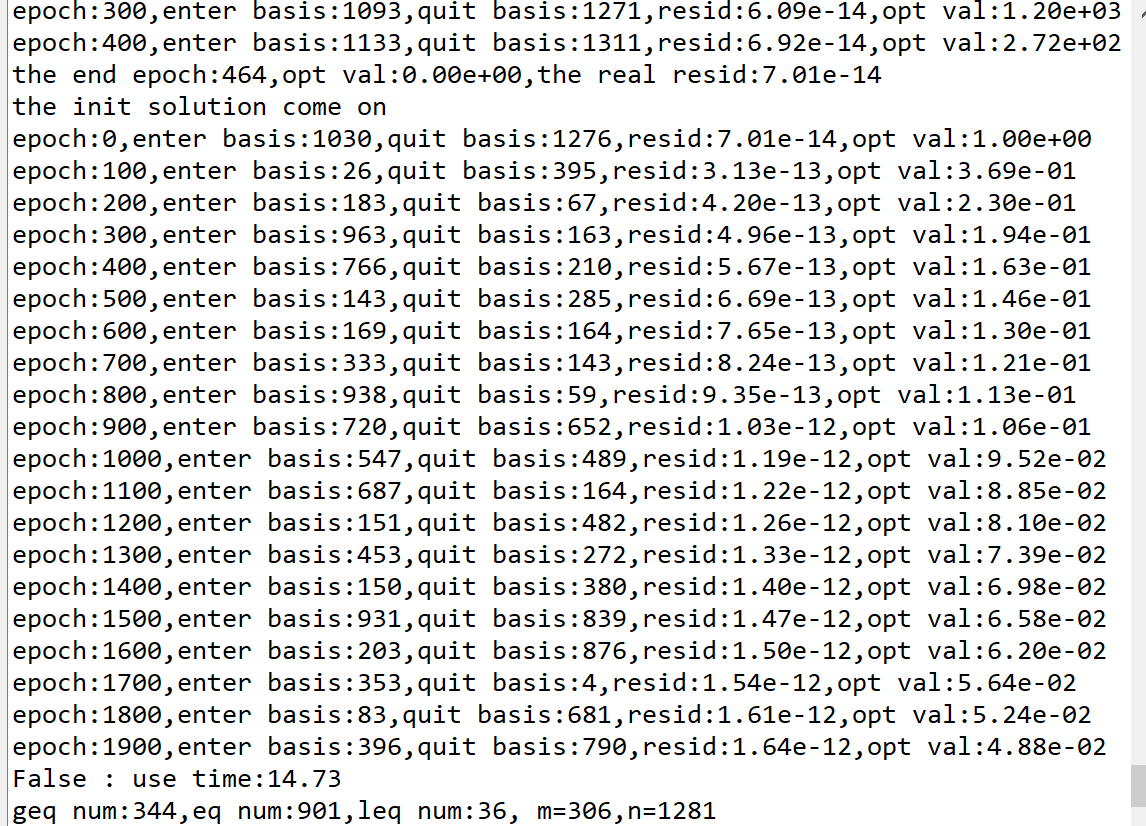
#L1 = 128
L1 = 64
P1 = 1024
k = 50
p = 0.02

np.random.seed(1)

# seed 1 with 512,1024, Danzig beats steepest
# seed 1 with 256, 512 steepest beats Danzig

R = np.random.binomial(1,p,[L1,P1])#Binomial distribution, generate [L1,P1] row array, all elements are 0 or 1
d = np.random.gamma(2,2,[k,1])*1#gamma distribution,
u = np.random.gamma(2,2,[L1,1])*3+20
s = P1 - k
ind = np.random.randint(0,k,s)#Randomly extract an integer between 0 and K
S = np.zeros((k,s))
for i in range(s):
    j = ind[i]
    S[j,i] = 1
S = np.hstack((np.identity(k),S))
n = P1+2*L1+1       #364
m = 2*L1+k          #196

# construct the vector c, only the last element is 1
c = np.zeros((n,1))
c[-1,0] = 1

# construct the matrix A
S1 = np.hstack((R,np.identity(L1),np.zeros((L1,L1)),np.zeros((L1,1))))
S2 = np.hstack((np.zeros((L1,P1)),np.identity(L1),-np.identity(L1),u))
S3 = np.hstack((S,np.zeros((k,(2*L1+1)))))
A = np.vstack((S1,S2,S3))


b = np.vstack((u,u,d))



#---------------------------------
L = R.shape[0];P = R.shape[1];K = S.shape[0]
m = 2*L + K;n = P + 2*L + 1
#print(type(R),type(S),type(u),type(d))
print(R.shape,S.shape,u.shape,d.shape)
print(max(R.reshape(-1,1)),min(R.reshape(-1,1)),max(S.reshape(-1,1)),min(S.reshape(-1,1)))
row1 = np.hstack([R,np.identity(L),np.zeros([L,L]),np.zeros([L,1])])
row2 = np.hstack([np.zeros([L,P]),np.identity(L),-np.identity(L),u])
row3 = np.hstack([S,np.zeros([K,2*L + 1])])
A = np.vstack([row1,row2,row3])
print(A.shape)
#print(np.linalg.matrix_rank(A),m)
b = np.vstack([u,u,d])
c = np.zeros([n,1]);c[-1,0] = 1.0
#piv = 'Bland'
#piv = 'Danzig'

st = time.time()
x = stage_two(c,A,b,L,P,K)
ela = time.time() - st

print(all(x >= 0),': use time:%.2f'%(ela))
geq = np.where(x > 0)[0]
eq = np.where(x == 0)[0]
leq = np.where(x < 0)[0]
print('geq num:%d,eq num:%d,leq num:%d, m=%d,n=%d'%(geq.size,eq.size,leq.size,m,n))
print('the nagetive element:')
print(x[leq])
#----------------------

singlesimplex.py

import numpy as np
import time
def Bland(s,indn):
    ind = np.where(s[:,0]<0)[0]
    q = ind[0]
    return indn[q], q

def DanzigSelect(s,indn):#indn non base index
    q = s.argmin()
    return indn[q], q

def SteepSelect(A_n,s,indn):
    ratio = s/A_n.transpose()
    q = ratio.argmin()
    return indn[q], q
def invB(B_inv,p,u):
    Bv = B_inv.copy()
    Bv[p,:] = Bv[p,:]/u[p,0]
    m = u.size
    ind = []
    for i in range(m):
        if i == p:
            pass
        else:
            ind.append(i)
            Bv[i,:] = Bv[i,:] - u[i,0]*Bv[p,:]
    ind.append(p)
    Bv = Bv[ind,:]
    return Bv
def stage_one(A,b,piv):#The large M method is used to solve the initial basic feasible solution
    eps = 1e-6
    [m,n] = A.shape
    x = np.zeros([n + m,1]);x[n:,:] = b
    
    Ah = np.hstack([A,np.identity(m)])
    ch =  np.zeros([n + m,1]);ch[n:,:] = np.ones([m,1])
    indb = np.arange(m + n)[n:]#Initial base index
    index = np.arange(0,m + n)
    indn = np.delete(index,indb)
    B = Ah[:,indb]#The initial B is the identity matrix
    B_inv = B
    
    N = Ah[:,indn]
    iteration = 0        # determine the max iteration
    
    while iteration < 1000:
        
        y = np.dot(B_inv.T, ch[indb,:])
        s = ch[indn,:] - N.T@y#C_N - N^TB^{-T}C_B
        if all(s >= 0):#It shows that this is the optimal solution
            print('unbelievabel,the resid:%.2e, done,the epoch:%d'%(np.linalg.norm(Ah@x - b),iteration))
            break
        if piv == 'Danzig':
            q1, q2 = DanzigSelect(s, indn)
        if piv == 'steepest-edge':
            A_re = B_inv@N
            A_n = np.linalg.norm(A_re,axis = 0,keepdims = True)
            q1, q2 = SteepSelect(A_n, s, indn)
        if piv == 'Bland':
            q1, q2 = Bland(s, indn)
        #q1 is the index that needs to be replaced in the non base index
        u = B_inv@Ah[:, q1:(q1+1)]   
        if all(u <= 0):#The optimal value is unbounded
            print('Linear program is unbounded.')
            break
            
        inds1 = np.where(u[:,0] > 0)[0]#Find all indexes greater than 0
        inds2 = indb[inds1]#Find all indexes corresponding to greater than 0 in the base index
        ratio = x[inds2,:]/u[inds1,:]
        x_q = min(ratio)        # a number
        p1 = inds2[ratio.argmin()]
        p2 = inds1[ratio.argmin()]
        
        x[indb,:] = x[indb,:]- x_q*u
        vec = np.zeros([indn.size,1])
        vec[q2,0] = x_q
        x[indn,:] = x[indn,:] + vec
        aug = np.linalg.norm(Ah@x - b)
        if aug > eps:
            print('blow up,epoch:%d,aug resid:%.2e'%(iteration,aug))
            break
        value = x[n:,:].sum()
        if iteration%100 == 0:
            
            print('epoch:%d,enter basis:%d,quit basis:%d,resid:%.2e,opt val:%.2e'
                  %(iteration,q1,p1,aug,value))
        
        if value < eps and all(s) >= 0:
            print('the end epoch:%d,opt val:%.2e,the real resid:%.2e'
                  %(iteration,value,np.linalg.norm(A@x[:n,:] - b)))
            break
        else:
            
            indb = np.delete(indb,p2)
            indb = np.append(indb,q1)
            
            indn = np.delete(indn,q2)
            indn = np.append(indn,p1)
            
            B = Ah[:, indb]
            B_inv = invB(B_inv,p2,u)
           
            N = Ah[:, indn]
            iteration = iteration + 1
    return x[:n]
def MCF(A,b,L,P,K):
    S = A[2*L:,:P]
    R = A[:L,:P]
    indb = []
    [m,n] = A.shape
    u = b[:L,:];d = b[2*L:,:]
    
    A1 = np.hstack([S,np.zeros([K,L])])
    A2 = np.hstack([R,np.identity(L)])
    Ar = np.vstack([A1,A2])
    br = np.vstack([d,u])
    x = np.zeros([n,1])
    x[:P + L,:] = stage_one(Ar,br,piv = 'Bland')
    geq = np.where(x[:P + L,:] > 0)[0]
    indb = np.append(indb,geq)
    #print(indb.size,K + L)
    if geq.size < K + L:
        radio = min(x[P:P + L,:]/u)
        M = 1.0 - radio# + 1e-2
        
        geq3 = np.arange(P + L,P + 2*L)
        indb = np.append(indb,geq3)
        if indb.size == K + 2*L - 1:
            pass
        else:
            er = K + 2*L - 1 - indb.size
            index = np.setdiff1d(np.arange(0,P + L),geq)
            ra = np.random.choice(index,er,replace = False)
            indb = np.append(indb,ra)
    else:
        radio = min(x[P:P + L,:]/u)
        ind = np.argmin(x[P:P + L,:]/u) + P + L
        geq3 = np.setdiff1d(np.arange(P + L,P + 2*L),ind)
        indb = np.append(indb,geq3)
        M = 1 - radio
    x[-1,0] = M
    indb = np.append(indb,P + 2*L)
    for i in range(L):
        x[P + L + i,0] = x[P + i,0] + (M - 1)*u[i,0]
    
    #print(indb.size)
    return x,indb
def stage_two(c,A,b,piv,L,P,K):
    eps = 1e-6
    [m,n] = A.shape
    x,indb = MCF(A,b,L,P,K)
    #print(x.shape,A.shape,b.shape,indb.size,m)
    if np.linalg.norm(A@x - b) > eps or (any(x < 0) and min(x) < -eps):
        print('the init solution error')
        return 0
    else:
        print('the init solution come on')
    
    indb = indb.astype('int32')
    index = np.arange(0,n)
    indn = np.delete(index,indb)
    B = A[:,indb]
    
    B_inv = np.linalg.inv(B)
    
    N = A[:,indn]
    iteration = 0        # determine the max iteration
    
    while iteration < 2000:
        y = np.dot(B_inv.T, c[indb,:])
        s = c[indn,:] - N.T@y#C_N - N^TB^{-T}C_B
        value = (c*x).sum()
        if all(s >= 0) or (any(s < 0) and min(s) > -eps):#It shows that this is the optimal solution
            print('the end epoch:%d,resid:%.2e,opt val:%.2e'
                  %(iteration,np.linalg.norm(A@x - b),value))
            break
        if piv == 'Danzig':
            q1, q2 = DanzigSelect(s, indn)
        if piv == 'steepest-edge':
            A_re = B_inv@N
            A_n = np.linalg.norm(A_re,axis = 0,keepdims = True)
            q1, q2 = SteepSelect(A_n, s, indn)
        if piv == 'Bland':
            q1, q2 = Bland(s, indn)
        #q1 is the index that needs to be replaced in the non base index
        u = B_inv@A[:, q1:(q1+1)]   
        if all(u <= 0):#The optimal value is unbounded
            print('Linear program is unbounded.')
            break
            
        inds1 = np.where(u[:,0] > 0)[0]#Find all indexes greater than 0
        inds2 = indb[inds1]#Find all indexes corresponding to greater than 0 in the base index
        ratio = x[inds2,:]/u[inds1,:]
        x_q = min(ratio)        # a number
        p1 = inds2[ratio.argmin()]
        p2 = inds1[ratio.argmin()]
        
        x[indb,:] = x[indb,:]- x_q*u
        vec = np.zeros([indn.size,1])
        vec[q2,0] = x_q
        x[indn,:] = x[indn,:] + vec
        res = np.linalg.norm(A@x - b)
        if res > eps:
            print('blow up,epoch:%d,resid:%.2e'%(iteration,res))
            break
        if iteration%100 == 0:
            #print(np.linalg.det(B))
            print('epoch:%d,enter basis:%d,quit basis:%d,resid:%.2e,opt val:%.2e'
                  %(iteration,q1,p1,res,value))
        indb = np.delete(indb,p2)
        indb = np.append(indb,q1)
            
        indn = np.delete(indn,q2)
        indn = np.append(indn,p1)
            
        B = A[:, indb]
        B_inv = invB(B_inv,p2,u)
           
        N = A[:, indn]
        iteration = iteration + 1
    return x




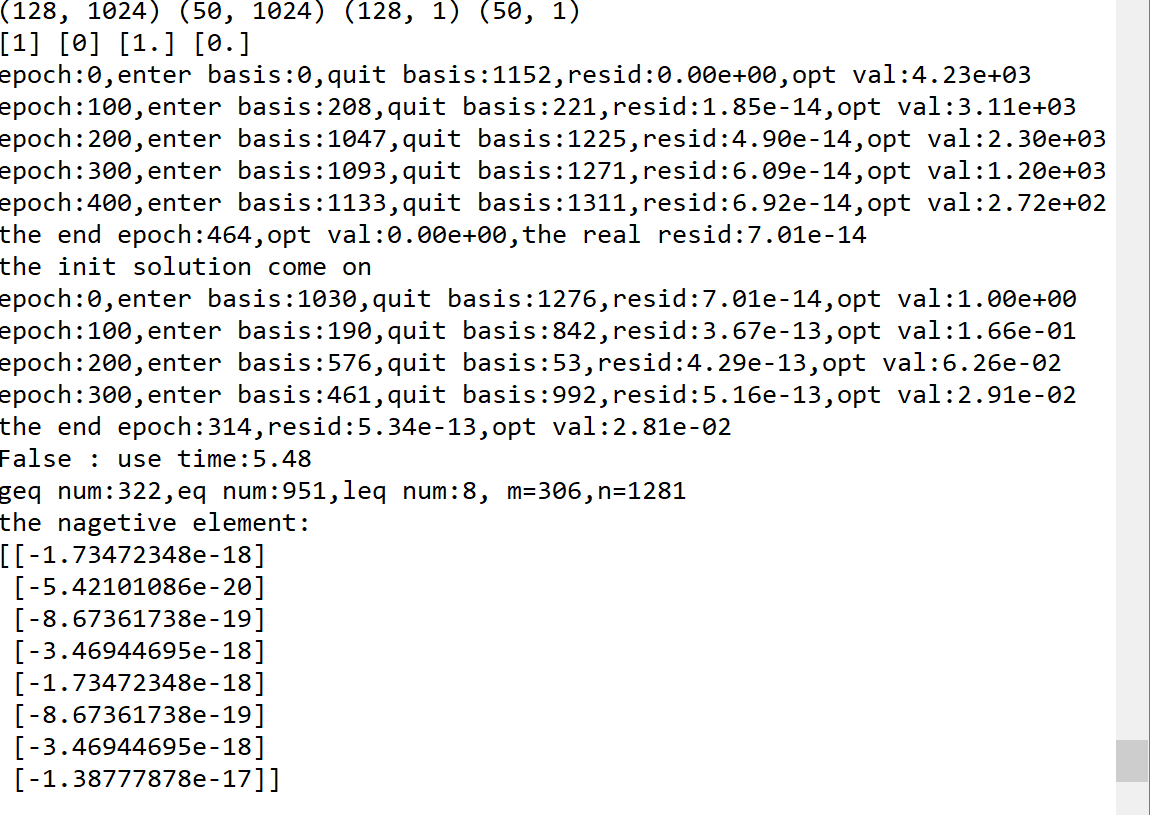
L1 = 128
P1 = 1024
k = 50
p = 0.02

np.random.seed(1)

# seed 1 with 512,1024, Danzig beats steepest
# seed 1 with 256, 512 steepest beats Danzig

R = np.random.binomial(1,p,[L1,P1])#Binomial distribution, generate [L1,P1] row array, all elements are 0 or 1
d = np.random.gamma(2,2,[k,1])*1#gamma distribution,
u = np.random.gamma(2,2,[L1,1])*3+20
s = P1 - k
ind = np.random.randint(0,k,s)#Randomly extract an integer between 0 and K
S = np.zeros((k,s))
for i in range(s):
    j = ind[i]
    S[j,i] = 1
S = np.hstack((np.identity(k),S))
n = P1+2*L1+1       #364
m = 2*L1+k          #196

# construct the vector c, only the last element is 1
c = np.zeros((n,1))
c[-1,0] = 1

# construct the matrix A
S1 = np.hstack((R,np.identity(L1),np.zeros((L1,L1)),np.zeros((L1,1))))
S2 = np.hstack((np.zeros((L1,P1)),np.identity(L1),-np.identity(L1),u))
S3 = np.hstack((S,np.zeros((k,(2*L1+1)))))
A = np.vstack((S1,S2,S3))


b = np.vstack((u,u,d))



#---------------------------------
L = R.shape[0];P = R.shape[1];K = S.shape[0]
m = 2*L + K;n = P + 2*L + 1
#print(type(R),type(S),type(u),type(d))
print(R.shape,S.shape,u.shape,d.shape)
print(max(R.reshape(-1,1)),min(R.reshape(-1,1)),max(S.reshape(-1,1)),min(S.reshape(-1,1)))
row1 = np.hstack([R,np.identity(L),np.zeros([L,L]),np.zeros([L,1])])
row2 = np.hstack([np.zeros([L,P]),np.identity(L),-np.identity(L),u])
row3 = np.hstack([S,np.zeros([K,2*L + 1])])
A = np.vstack([row1,row2,row3])
#print(np.linalg.matrix_rank(A),m)
b = np.vstack([u,u,d])
c = np.zeros([n,1]);c[-1,0] = 1.0
#piv = 'Bland'
piv = 'Danzig'

st = time.time()
x = stage_two(c,A,b,piv,L,P,K)
ela = time.time() - st

print(all(x >= 0),': use time:%.2f'%(ela))
geq = np.where(x > 0)[0]
eq = np.where(x == 0)[0]
leq = np.where(x < 0)[0]
print('geq num:%d,eq num:%d,leq num:%d, m=%d,n=%d'%(geq.size,eq.size,leq.size,m,n))
print('the nagetive element:')
print(x[leq])
#----------------------

multisimplex.py

import numpy as np
import time
def Bland(s,indn):
    ind = np.where(s[:,0]<0)[0]
    q = ind[0]
    return indn[q], q

def DanzigSelect(s,indn):#indn non base index
    q = s.argmin()
    return indn[q], q

def SteepSelect(A_n,s,indn):
    ratio = s/A_n.transpose()
    q = ratio.argmin()
    return indn[q], q
def invB(B_inv,p,u):
    Bv = B_inv.copy()
    Bv[p,:] = Bv[p,:]/u[p,0]
    m = u.size
    ind = []
    for i in range(m):
        if i == p:
            pass
        else:
            ind.append(i)
            Bv[i,:] = Bv[i,:] - u[i,0]*Bv[p,:]
    ind.append(p)
    Bv = Bv[ind,:]
    return Bv
def stage_one(A,b,piv):#The large M method is used to solve the initial basic feasible solution
    eps = 1e-6
    [m,n] = A.shape
    x = np.zeros([n + m,1]);x[n:,:] = b
    
    Ah = np.hstack([A,np.identity(m)])
    ch =  np.zeros([n + m,1]);ch[n:,:] = np.ones([m,1])
    indb = np.arange(m + n)[n:]#Initial base index
    index = np.arange(0,m + n)
    indn = np.delete(index,indb)
    B = Ah[:,indb]#The initial B is the identity matrix
    B_inv = B
    
    N = Ah[:,indn]
    iteration = 0        # determine the max iteration
    
    while iteration < 1000:
        
        y = np.dot(B_inv.T, ch[indb,:])
        s = ch[indn,:] - N.T@y#C_N - N^TB^{-T}C_B
        if all(s >= 0):#It shows that this is the optimal solution
            print('unbelievabel,the resid:%.2e, done,the epoch:%d'%(np.linalg.norm(Ah@x - b),iteration))
            break
        if piv == 'Danzig':
            q1, q2 = DanzigSelect(s, indn)
        if piv == 'steepest-edge':
            A_re = B_inv@N
            A_n = np.linalg.norm(A_re,axis = 0,keepdims = True)
            q1, q2 = SteepSelect(A_n, s, indn)
        if piv == 'Bland':
            q1, q2 = Bland(s, indn)
        #q1 is the index that needs to be replaced in the non base index
        u = B_inv@Ah[:, q1:(q1+1)]   
        if all(u <= 0):#The optimal value is unbounded
            print('Linear program is unbounded.')
            break
            
        inds1 = np.where(u[:,0] > 0)[0]#Find all indexes greater than 0
        inds2 = indb[inds1]#Find all indexes corresponding to greater than 0 in the base index
        ratio = x[inds2,:]/u[inds1,:]
        x_q = min(ratio)        # a number
        p1 = inds2[ratio.argmin()]
        p2 = inds1[ratio.argmin()]
        
        x[indb,:] = x[indb,:]- x_q*u
        vec = np.zeros([indn.size,1])
        vec[q2,0] = x_q
        x[indn,:] = x[indn,:] + vec
        aug = np.linalg.norm(Ah@x - b)
        if aug > eps:
            print('blow up,epoch:%d,aug resid:%.2e'%(iteration,aug))
            break
        value = x[n:,:].sum()
        if iteration%100 == 0:
            
            print('epoch:%d,enter basis:%d,quit basis:%d,resid:%.2e,opt val:%.2e'
                  %(iteration,q1,p1,aug,value))
        
        if value < eps:
            print('the end epoch:%d,opt val:%.2e,the real resid:%.2e'
                  %(iteration,value,np.linalg.norm(A@x[:n,:] - b)))
            break
        else:
            
            indb = np.delete(indb,p2)
            indb = np.append(indb,q1)
            
            indn = np.delete(indn,q2)
            indn = np.append(indn,p1)
            
            B = Ah[:, indb]
            B_inv = invB(B_inv,p2,u)
           
            N = Ah[:, indn]
            iteration = iteration + 1
    return x[:n,:]
def MCF(A,b,L,P,K):
    S = A[2*L:,:P]
    R = A[:L,:P]
    indb = []
    [m,n] = A.shape
    u = b[:L,:];d = b[2*L:,:]
    
    A1 = np.hstack([S,np.zeros([K,L])])
    A2 = np.hstack([R,np.identity(L)])
    Ar = np.vstack([A1,A2])
    br = np.vstack([d,u])
    x = np.zeros([n,1])
    x[:P + L,:] = stage_one(Ar,br,piv = 'Bland')
    geq = np.where(x[:P + L,:] > 0)[0]
    indb = np.append(indb,geq)
    #print(indb.size,K + L)
    if geq.size < K + L:
        radio = min(x[P:P + L,:]/u)
        M = 1.0 - radio# + 1e-2
        
        geq3 = np.arange(P + L,P + 2*L)
        indb = np.append(indb,geq3)
        if indb.size == K + 2*L - 1:
            pass
        else:
            er = K + 2*L - 1 - indb.size
            index = np.setdiff1d(np.arange(0,P + L),geq)
            ra = np.random.choice(index,er,replace = False)
            indb = np.append(indb,ra)
    else:
        radio = min(x[P:P + L,:]/u)
        ind = np.argmin(x[P:P + L,:]/u) + P + L
        geq3 = np.setdiff1d(np.arange(P + L,P + 2*L),ind)
        indb = np.append(indb,geq3)
        M = 1 - radio
    x[-1,0] = M
    indb = np.append(indb,P + 2*L)
    for i in range(L):
        x[P + L + i,0] = x[P + i,0] + (M - 1)*u[i,0]
    
    #print(indb.size)
    return x,indb
def stage_two(c,A,b,L,P,K):
    eps = 1e-6
    [m,n] = A.shape
    x,indb = MCF(A,b,L,P,K)
    
    if np.linalg.norm(A@x - b) > eps or (any(x < 0) and min(x) < -eps):
        print('the init solution error')
        return 0
    else:
        print('the init solution come on')
    
    indb = indb.astype('int32')
    index = np.arange(0,n)
    indn = np.delete(index,indb)
    B = A[:,indb]
    
    B_inv = np.linalg.inv(B)
    
    N = A[:,indn]
    iteration = 0        # determine the max iteration
    value = 0
    while iteration < 2000:
        y = np.dot(B_inv.T, c[indb,:])
        s = c[indn,:] - N.T@y#C_N - N^TB^{-T}C_B
        
        if all(s >= 0) or (any(s < 0) and min(s) > -eps):#It shows that this is the optimal solution
            print('the end epoch:%d,resid:%.2e,opt val:%.2e'
                  %(iteration,np.linalg.norm(A@x - b),value))
            break
        xd = x.copy()
        xs = x.copy()
        xb = x.copy()
        allx = []
        allq = []
        allp = []
        allu = []
        allval = []
        #------------------------
        q1, q2 = DanzigSelect(s, indn)
        allq.append(q1)
        allq.append(q2)
        u = B_inv@A[:, q1:(q1+1)]
        inds1 = np.where(u[:,0] > 0)[0]#Find all indexes greater than 0
        inds2 = indb[inds1]#Find all indexes corresponding to greater than 0 in the base index
        ratio = xd[inds2,:]/u[inds1,:]
        x_q = min(ratio)        # a number
        p1 = inds2[ratio.argmin()]
        p2 = inds1[ratio.argmin()]
        allp.append(p1)
        allp.append(p2)
        xd[indb,:] = xd[indb,:]- x_q*u
        vec = np.zeros([indn.size,1])
        vec[q2,0] = x_q
        xd[indn,:] = xd[indn,:] + vec
        
        val = (c*xd).sum()
        
        allx.append(xd)
        
        allu.append(u)
        allval.append(val)
        #------------------------
        A_re = B_inv@N
        A_n = np.linalg.norm(A_re,axis = 0,keepdims = True)
        q1, q2 = SteepSelect(A_n, s, indn)
        allq.append(q1)
        allq.append(q2)
        u = B_inv@A[:, q1:(q1+1)]
        inds1 = np.where(u[:,0] > 0)[0]#Find all indexes greater than 0
        inds2 = indb[inds1]#Find all indexes corresponding to greater than 0 in the base index
        ratio = xs[inds2,:]/u[inds1,:]
        x_q = min(ratio)        # a number
        p1 = inds2[ratio.argmin()]
        p2 = inds1[ratio.argmin()]
        allp.append(p1)
        allp.append(p2)
        xs[indb,:] = xs[indb,:]- x_q*u
        vec = np.zeros([indn.size,1])
        vec[q2,0] = x_q
        xs[indn,:] = xs[indn,:] + vec
        
        val = (c*xs).sum()
        
        allx.append(xs)
        
        allu.append(u)
        allval.append(val)
        #-------------------------
        q1, q2 = Bland(s, indn)
        allq.append(q1)
        allq.append(q2)
        u = B_inv@A[:, q1:(q1+1)]
        inds1 = np.where(u[:,0] > 0)[0]#Find all indexes greater than 0
        inds2 = indb[inds1]#Find all indexes corresponding to greater than 0 in the base index
        ratio = xb[inds2,:]/u[inds1,:]
        x_q = min(ratio)        # a number
        p1 = inds2[ratio.argmin()]
        p2 = inds1[ratio.argmin()]
        allp.append(p1)
        allp.append(p2)
        xb[indb,:] = xb[indb,:]- x_q*u
        vec = np.zeros([indn.size,1])
        vec[q2,0] = x_q
        xb[indn,:] = xb[indn,:] + vec
        
        val = (c*xb).sum()
        
        allx.append(xb)
        
        allu.append(u)
        allval.append(val)
        #----------------
        mind = np.argmin(allval)
        u = allu[mind]
        x = allx[mind]
        
        value = allval[mind]
        q1,q2 = allq[2*mind],allq[2*mind + 1]
        p1,p2 = allp[2*mind],allp[2*mind + 1]
        allu.clear();allx.clear();allval.clear();allq.clear();allp.clear()
        #q1 is the index that needs to be replaced in the non base index
        if all(u <= 0):#The optimal value is unbounded
            print('Linear program is unbounded.')
            break
        res = np.linalg.norm(A@x - b)
        if res > eps:
            print('blow up,epoch:%d,resid:%.2e'%(iteration,res))
            break
        if iteration%100 == 0:
            #print(np.linalg.det(B))
            print('epoch:%d,enter basis:%d,quit basis:%d,resid:%.2e,opt val:%.2e'
                  %(iteration,q1,p1,res,value))
        indb = np.delete(indb,p2)
        indb = np.append(indb,q1)
            
        indn = np.delete(indn,q2)
        indn = np.append(indn,p1)
            
        B = A[:, indb]
        B_inv = invB(B_inv,p2,u)
           
        N = A[:, indn]
        iteration = iteration + 1
    return x






L1 = 128
P1 = 1024
k = 50
p = 0.02

np.random.seed(1)

# seed 1 with 512,1024, Danzig beats steepest
# seed 1 with 256, 512 steepest beats Danzig

R = np.random.binomial(1,p,[L1,P1])#Binomial distribution, generate [L1,P1] row array, all elements are 0 or 1
d = np.random.gamma(2,2,[k,1])*1#gamma distribution,
u = np.random.gamma(2,2,[L1,1])*3+20
s = P1 - k
ind = np.random.randint(0,k,s)#Randomly extract an integer between 0 and K
S = np.zeros((k,s))
for i in range(s):
    j = ind[i]
    S[j,i] = 1
S = np.hstack((np.identity(k),S))
n = P1+2*L1+1       #364
m = 2*L1+k          #196

# construct the vector c, only the last element is 1
c = np.zeros((n,1))
c[-1,0] = 1

# construct the matrix A
S1 = np.hstack((R,np.identity(L1),np.zeros((L1,L1)),np.zeros((L1,1))))
S2 = np.hstack((np.zeros((L1,P1)),np.identity(L1),-np.identity(L1),u))
S3 = np.hstack((S,np.zeros((k,(2*L1+1)))))
A = np.vstack((S1,S2,S3))


b = np.vstack((u,u,d))


#---------------------------------
L = R.shape[0];P = R.shape[1];K = S.shape[0]
m = 2*L + K;n = P + 2*L + 1
#print(type(R),type(S),type(u),type(d))
print(R.shape,S.shape,u.shape,d.shape)
print(max(R.reshape(-1,1)),min(R.reshape(-1,1)),max(S.reshape(-1,1)),min(S.reshape(-1,1)))
row1 = np.hstack([R,np.identity(L),np.zeros([L,L]),np.zeros([L,1])])
row2 = np.hstack([np.zeros([L,P]),np.identity(L),-np.identity(L),u])
row3 = np.hstack([S,np.zeros([K,2*L + 1])])
A = np.vstack([row1,row2,row3])
#print(np.linalg.matrix_rank(A),m)
b = np.vstack([u,u,d])
c = np.zeros([n,1]);c[-1,0] = 1.0

st = time.time()
x = stage_two(c,A,b,L,P,K)
ela = time.time() - st

print(all(x >= 0),': use time:%.2f'%(ela))
geq = np.where(x > 0)[0]
eq = np.where(x == 0)[0]
leq = np.where(x < 0)[0]
print('geq num:%d,eq num:%d,leq num:%d, m=%d,n=%d'%(geq.size,eq.size,leq.size,m,n))
#print(geq.size,eq.size,leq.size,m)
print('the nagetive element:')
print(x[leq])
#----------------------