The Qin Jiuzhao algorithm is used to solve the value of exponential continuous growth polynomials by using recursive method. The efficiency of this algorithm is 10 times higher than that of the one-item algorithm, which multiplies from the innermost layer to the outermost layer.

The idea here is basically the same as Qin Jiuzhao's algorithm. The only difference is that the difference between two adjacent exponents of sparse polynomials is not 1, but an uncertain number.

In addition, using recursive algorithm to calculate the value of sparse polynomials is not recommended to use the method of function call, because if the maximum exponent is large, the program will collapse, and when we calculate a polynomial, take a polynomial of books (data structure is strict and sensitive version) for example, the exponent has more than 2000, so I think we need to change to the mode of cycle.

The following picture is my sketch when I think about solving sparse polynomials with recursive algorithm. I am dull, and I have used many examples to think about it. Here is just one of them. I hope it will inspire you.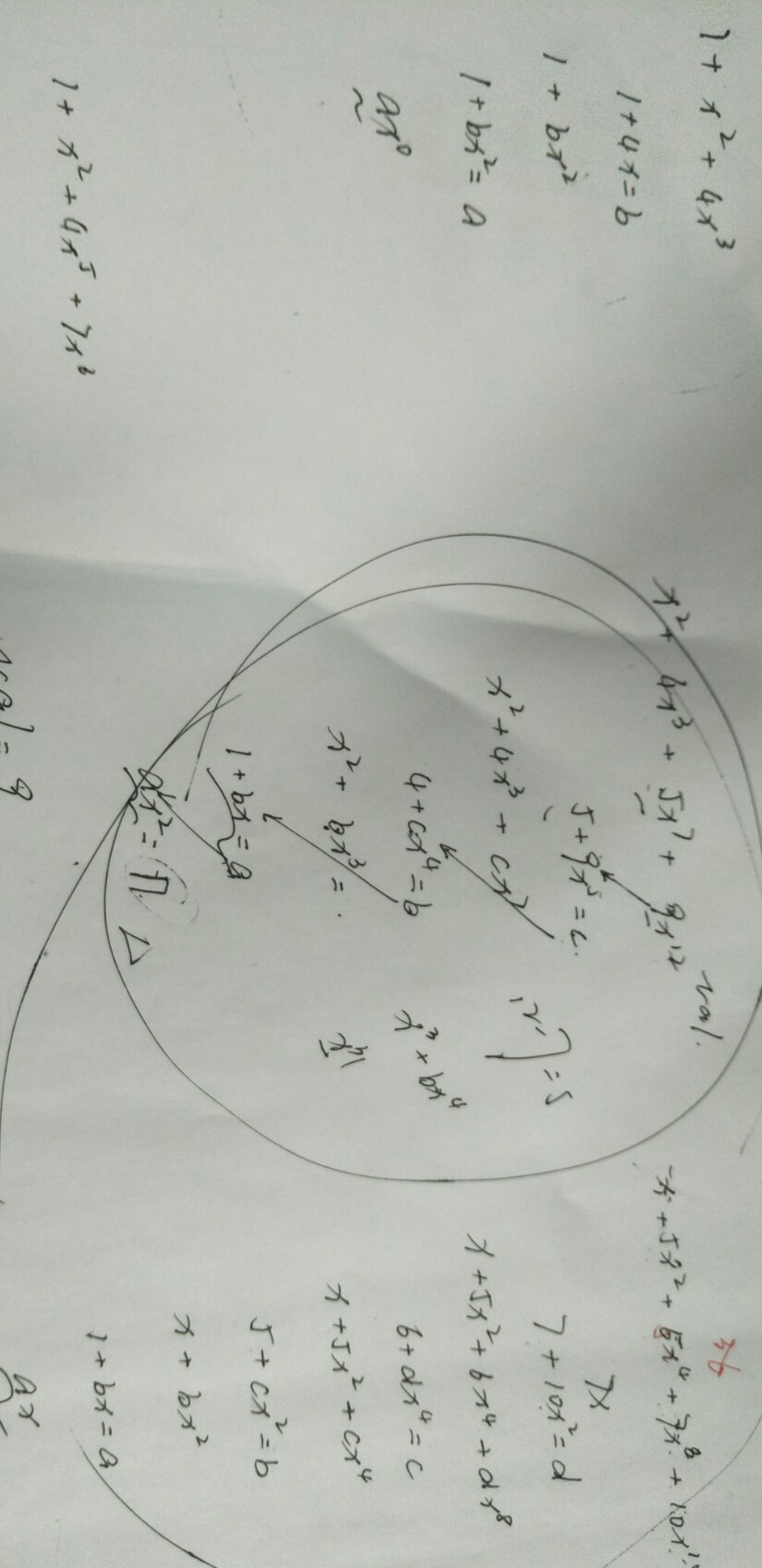

Here is the code. The last function is the recursive algorithm. The other functions just help to construct the polynomial of the test. I hope they can help you.

#include<stdio.h>
#include<malloc.h>
#include<assert.h>
#define SIZE 20

typedef struct
{
    double ceof;
    int    expn;
}Polyterm;
typedef struct PolySList
{
    Polyterm *data;
    int length;
}List;

void initial(List *list);
void insert(List *list,double ceof,int expn);
void show(List *list);
double calculate(List *list,double x);

int main()
{
    List list;
    initial(&list);

    printf("Now create this polynomial to calculate the value(Input coefficients and exponents in turn.-1 End)\n");
    double ceof;
    int expn;
    while(1)
    {
        scanf("%lf%d",&ceof,&expn);
        if(ceof==-1)
            break;
        insert(&list,ceof,expn);
    }
    printf(">>>");
    show(&list);

    printf("Please enter a value to calculate\n");
    double x;
    scanf("%lf",&x);
    printf("The result is:%.2lf\n",calculate(&list,x));

    return(1);
}

void initial(List *list)
{//The function of this algorithm is to initialize a sequence table.
    list->data=(Polyterm*)malloc(SIZE*sizeof(Polyterm));
    assert(list->data!=NULL);

    list->length=0;//The number of terms of a polynomial is 0
}

void insert(List *list,double ceof,int expn)
{//The premise of this algorithm is that the sequence table has been initialized and the sequence table is not full.
    //The function of this algorithm is to insert items consisting of ceof and expn into the sequence table.
    //And keep polynomials in exponential increasing order
    int i=0,j;

    while(i<list->length && list->data[i].expn<expn)
        i++;

    if(list->data[i].expn==expn)
    {
        list->data[i].ceof+=ceof;
        if(list->data[i].ceof==0)//If it happens to offset
        {
            for(j=i;j<list->length-1;--j)
            {
                list->data[j].ceof=list->data[j+1].ceof;
                list->data[j].expn=list->data[j+1].expn;
            }
            list->length--;
        }
    }
    else
    {
        for(j=list->length;j>i;--j)
        {
            list->data[j].ceof=list->data[j-1].ceof;
            list->data[j].expn=list->data[j-1].expn;
        }
        list->data[i].ceof=ceof;
        list->data[i].expn=expn;
        list->length++;
    }
}

void show(List *list)
{//The premise of this algorithm is that there is at least one item in the polynomial.
    //The function of this algorithm is to display polynomials.
    if(list->length==0)
        return;//Judgment of Legitimacy of Polynomial Length

    for(int i=0;i<list->length;i++)
    {
        printf("%.2lfx^%d+",list->data[i].ceof,list->data[i].expn);
    }
    printf("\b \n");
}

double calculate(List *list,double x)
{//The premise of this algorithm is that there is at least one item in the polynomial.
    //The function of this algorithm is to calculate the value of the polynomial according to the parameter x and return the value.
    double val;
    int i,j;

    val=list->data[list->length-1].ceof;
    for(i=list->length-1;i>=1;--i)
    {
        double t=1;
        for(j=list->data[i].expn-list->data[i-1].expn;j>0;--j) //Recursive thinking for calculating the value of polynomials
            t*=x;
        val=list->data[i-1].ceof+val*t;
    }

    double t=1;
    for(i=list->data[0].expn;i>0;--i)
        t*=x;

    return(val*t);
}