Some common methods of mathematical modeling
1. The analytical hierarchy process (AHP)
- Modeling is one of the most basic models in the competition, which is mainly used to solve evaluation problems (for example, select which scheme is the best, which athlete or employee performs better)
- Through the relevant weight, the score is calculated to obtain the optimal solution
1.1 disadvantages of asking weight directly
The main difficulty in determining the proportion of factors affecting a factor is that these proportions are often difficult to quantify. In addition, when there are many factors affecting a factor, when directly considering the impact of each factor on the factor, the decision-maker will often put forward data inconsistent with his actual importance, or even put forward a group of implicitly contradictory data due to incomplete consideration and loss of one or the other.
——Selected from mathematical modeling algorithm and application by Mr. Si Shoukui [ku í]
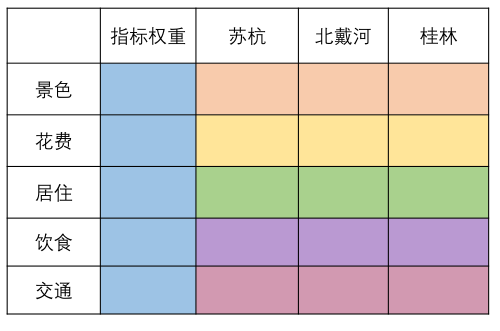
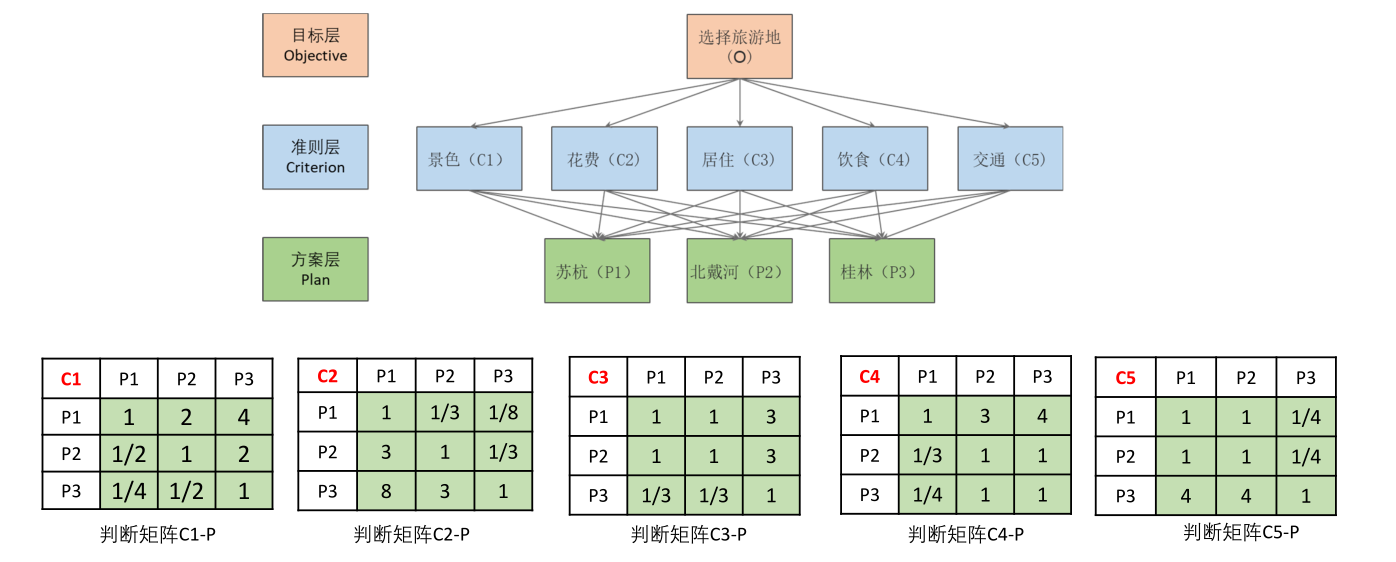
Analytic hierarchy process
- The relationship between the factors in the system is analyzed and the hierarchical structure of the system is established
- Compare the importance of each element in the same level with respect to a criterion in the previous level, and construct a pairwise comparison matrix (judgment matrix)
- The relative weight of the compared element to the criterion is calculated from the judgment matrix, and the consistency test is carried out (it can be used only after passing the weight test)
- The scores are calculated and sorted according to the weight matrix.
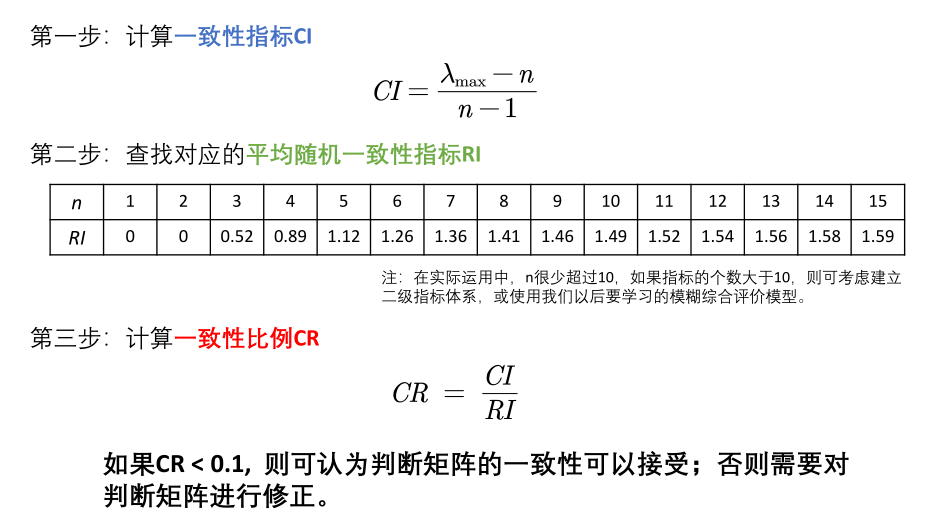
1.2 steps of conformance inspection
Find the maximum eigenvalue λ
The function of eigenvalue D and eigenvector V of matrix A is eig(A)
clc
n = size(A,1)
[V,D] = eig(A) %V Is the eigenvector, D Is a diagonal matrix composed of eigenvalues (except diagonal elements, all other position elements are 0)
Max_eig = max(max(D)) %It can also be written as max(D(:))
CI = (Max_eig - n) / (n-1);
RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; %Attention, here RI Maximum support n = 15
CR=CI/RI(n);
disp('Consistency index CI=');disp(CI);
disp('Consistency ratio CR=');disp(CR);
if CR<0.10
disp('because CR < 0.10,So the judgment matrix A The consistency of is acceptable!');
else
disp('be careful: CR >= 0.10,Therefore, the judgment matrix A It needs to be modified!');
end
V = 0.4058 + 0.0000i 0.0914 - 0.2754i 0.0914 + 0.2754i 0.7071 + 0.0000i -0.2298 + 0.0000i 0.4058 + 0.0000i 0.0914 - 0.2754i 0.0914 + 0.2754i -0.7071 + 0.0000i -0.2298 + 0.0000i 0.1299 + 0.0000i 0.0268 + 0.1349i 0.0268 - 0.1349i 0.0000 + 0.0000i -0.3457 + 0.0000i 0.7872 + 0.0000i -0.8930 + 0.0000i -0.8930 + 0.0000i -0.0000 + 0.0000i 0.6897 + 0.0000i 0.1847 + 0.0000i 0.1131 + 0.0490i 0.1131 - 0.0490i -0.0000 + 0.0000i 0.5470 + 0.0000i D = 5.2924 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.0843 + 1.2326i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.0843 - 1.2326i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.1238 + 0.0000i
How to correct if CR > 0.1?
- Adjust the rows of the consistency matrix to the consistency matrix to form a multiple relationship
1.3 three methods to calculate weight
Arithmetic mean method
% Step 1: normalize the judgment matrix according to columns (divide each element by the sum of its columns)
Sum_A = sum(A)
[n,n] = size(A) % It can also be written as n = size(A,1)
% Because our judgment matrix A It's a square array, so here r and c The same, we can use the same letter n express
SUM_A = repmat(Sum_A,n,1) %repeat matrix Abbreviation of
% Another alternative method is as follows:
SUM_A = [];
for i = 1:n %Loop Oh, this line cannot be followed by a colon (and) Python Different), here it represents a cycle n second
SUM_A = [SUM_A; Sum_A]
end
clc;A
SUM_A
Stand_A = A ./ SUM_A
% Here we can directly divide the corresponding elements of the two matrices
% Step 2: add the normalized columns(Sum by row)
sum(Stand_A,2)
% Step 3: divide each element in the added vector by n You can get the weight vector
disp('The result of weight calculation by arithmetic average method is:');
disp(sum(Stand_A,2) / n)
% Firstly, the normalized matrix is summed according to rows to obtain a column vector
% Then divide each element of the column vector by n Yes (note that it can also be used here./Oh)
Geometric average method
% Step 1: transfer A The elements of are multiplied by rows to get a new column vector
clc;A
Prduct_A = prod(A,2)
% prod Function sum sum Functions are similar, one for multiplication and one for addition dim = 2 Dimensions are rows
% Step 2: open each component of the new vector n Power
Prduct_n_A = Prduct_A .^ (1/n)
% Here, the power operation is performed on each element, so it is necessary to add.No. ^The sign means power. Oh, this is open n Power, so we find 1 equivalently/n Power
% Step 3: normalize the column vector to obtain the weight vector
% Divide each element in this column vector by the sum of this vector
disp('The weight obtained by geometric average method is:');
disp(Prduct_n_A ./ sum(Prduct_n_A))
Eigenvalue method
% Step 1: find the matrix A The maximum eigenvalue of and its corresponding eigenvector
clc
[V,D] = eig(A) %V Is the eigenvector, D Is a diagonal matrix composed of eigenvalues (except diagonal elements, all other position elements are 0)
Max_eig = max(max(D)) %It can also be written as max(D(:))
% So how to find the location of the maximum eigenvalue? Need to use find Function, which can be used to return the position index of non-zero elements in a vector or matrix.
% Then the problem comes. To get the position of the maximum eigenvalue, we need to put the diagonal matrix containing all eigenvalues D In, all positions that are not equal to the maximum eigenvalue become 0
% At this time, the size judgment operation of matrix and constant can be used
D == Max_eig
[r,c] = find(D == Max_eig , 1)
% find D The position of the first element equal to the maximum eigenvalue in, recording its row and column.
% Step 2: normalize the feature vector to get our weight
V(:,c)
disp('The result of weight calculation by eigenvalue method is:');
disp( V(:,c) ./ sum(V(:,c)) )
% Let's start with the number of columns with the maximum eigenvalue found above c Find the corresponding eigenvector, and then standardize it.
Note: consistency test is not required for consistency matrix, but only for judgment matrix of non consistency matrix; In thesis writing, consistency test should be carried out first, and then the weight should be calculated after passing the test
1.4 some limitations of analytic hierarchy process
- There should not be too many decision-making levels for evaluation. If there are too many, n will be very large, and the difference between judgment matrix and consistency matrix may be very large.
