

That has changed, that is, linear lists and linked lists only go online. Offline can't go online in violation of supervision. This is very bad. What we need is mutual supervision between online and offline.
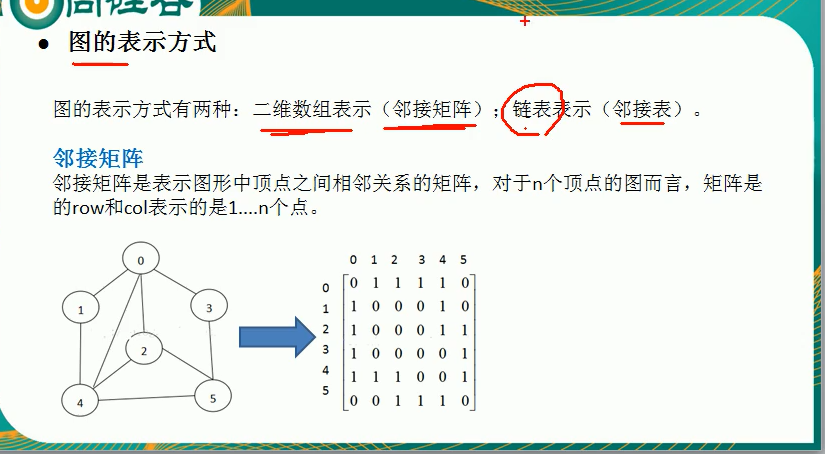
This is an undirected graph, which is connected with each other. A - B = 1 and B - a = 1 mean that they are connected with each other.
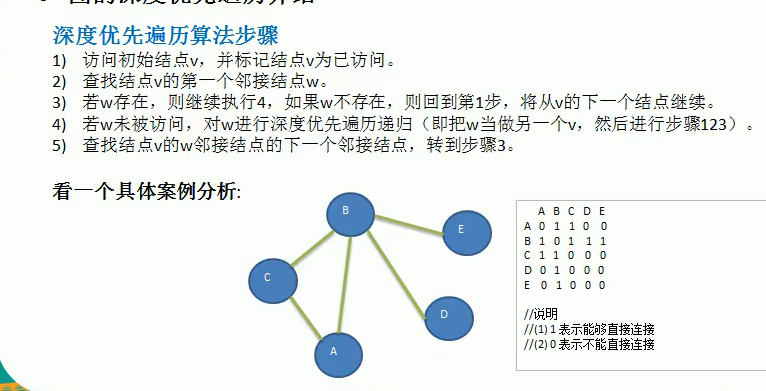
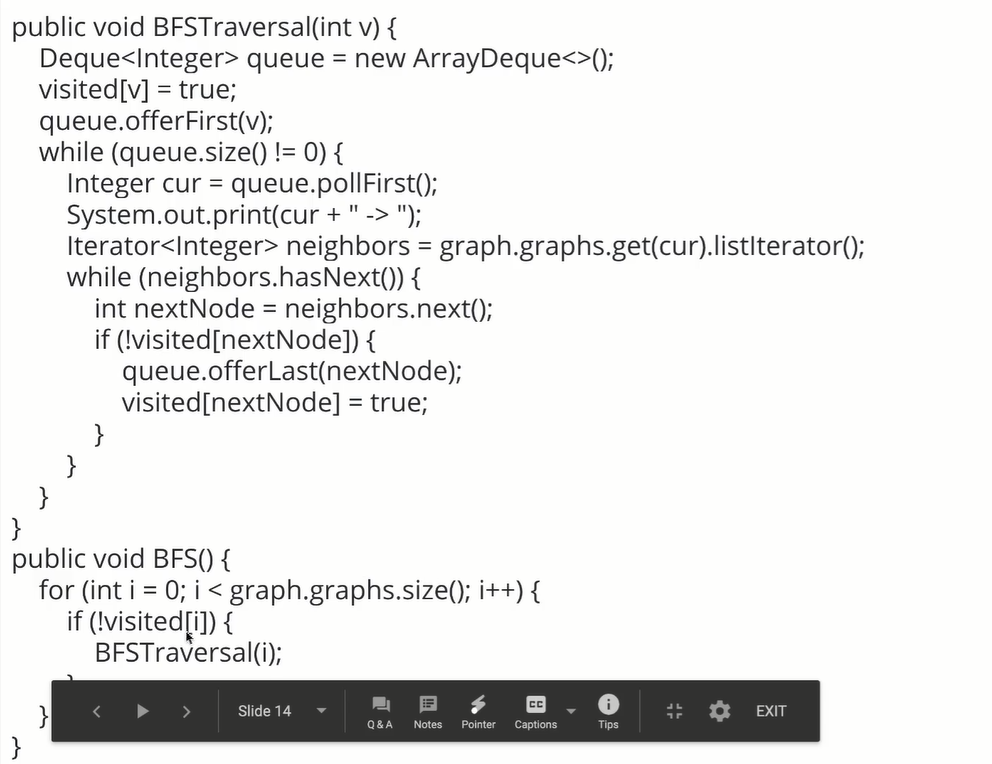
Breadth first is stupid. It is to get all adjacent nodes of a node, print yourself and all adjacent nodes after entering, and then set these nodes as accessed.
Then send all nodes to perform the above operations (judge whether they have been accessed before execution, and send them to perform the above operations as long as they have not been accessed)
Through the adjacency matrix, the depth first and breadth first topics have been completed
package org.example.sort;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
public class Graph {
private ArrayList<String> vertexList;
private int[][] edges;//Record matrix
private int numOfedes;//Number of edges
private boolean[] visited;//Determines whether the current node has been accessed
public static void main(String[] args) {
//Test one
//Set the number of nodes first
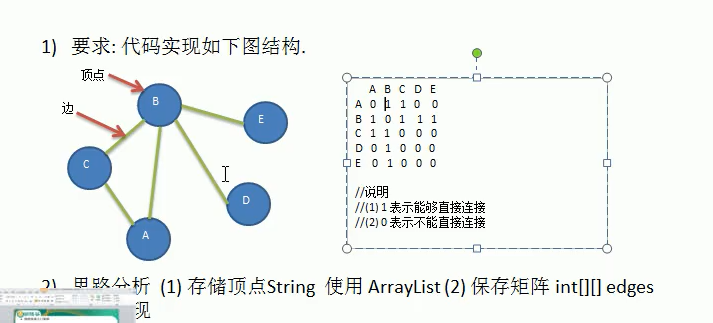
int n = 5;
String[] Vertesx = {"a","b","c","d","e"};//Set vertex
Graph graph = new Graph(n);
for(String tex : Vertesx){
graph.insert(tex);
}//Add vertices to the graph
//A - B A- c B - C B - D B - E
graph.insertedges(0,1,1);
graph.insertedges(0,2,1);
graph.insertedges(1,2,1);
graph.insertedges(1,3,1);
graph.insertedges(1,4,1);
graph.bfs();
}
public Graph(int n){
//Initialization matrix
edges = new int[n][n];
vertexList = new ArrayList<>(n);
numOfedes = 0;
//Don't forget to record the size of the access node during initialization
visited = new boolean[n];//Create the size of this variable at any time
}
//Implementation breadth first
public void bfs(){
for (int i = 0;i < getNumOfedes();i++){
if(!visited[i]){
//Perform breadth first as long as you haven't been visited
bfsNode(i);
}
}
}
//Breadth first execution steps
private void bfsNode(int i){
visited[i] = true;//Coming in means you're being interviewed
System.out.print(getValueOfIndex(i) + "-> ");//Print yourself
//breadth-first search
//First, all the adjacency tables of the current node are accessed
//A queue is needed to control all this. The queue queues all the visited child nodes of the current node one by one
//After all child nodes have been accessed, all child nodes are taken out of the queue and accessed recursively. The child nodes of each child node have been accessed, and each node maintains a queue
//Keep control of your child nodes
//Print all child nodes first
for(Integer num : getAllNeighbor(i)){
if(!visited[num]){
System.out.print(getValueOfIndex(num) + "->");
visited[num] = true;//Settings have been accessed
}
}
}
//Obtain all adjacent nodes of the current node according to the index
public ArrayList<Integer> getAllNeighbor(int index){
ArrayList<Integer> result = new ArrayList<>();
for(int i = 0;i < getNumOfedes();i++){
if(edges[index][i] != 0){
//Description Unicom
result.add(i);
}
}
return result;//Integrate all adjacency points together
}
//Can go into traversal to illustrate this; Is reliable
public void dfs(int i){//Every time a subscript is passed in
//Depth first traversal
System.out.print(getValueOfIndex(i) + "->");//Print the current node value
visited[i] = true;//Indicates that this point has been traversed
//After printing, see if there are adjacent points
int next = getFirstNeighbor(i);//Find neighbor nodes
//After this point access is completed, find the adjacent point
while (next != -1){
//Indicates that there is an adjacent contact
if(!visited[next]){
dfs(next);//If the adjacent node is not accessed, access it
}
//Access the next adjacent node and go back to access the next adjacent node
next = getNextNeighbor(i,next);//Find the next adjacent contact to see if it has not been visited
}
//Indicates that there are adjacent nodes
//Direct traversal of adjacent nodes
}
//Get first neighbor subscript
//No neighbors will return - 1
public int getFirstNeighbor(int index){
//Gets the subscript of the first neighbor of the current node
//Depth first traversal
//I will give you the subscript of the node to be queried. You traverse the entire adjacency matrix table. If you encounter the one with edge 1, you will return the column. That column subscript is the first adjacency point
for(int j = 0;j < vertexList.size();j++){
if(edges[index][j] == 1){
//An adjacent contact was found
return j;//Return the adjacent node index
}
}
return -1;//After traversing the whole line, it does not return, indicating that there is no adjacency point. At this time, returning - 1 indicates that there is no adjacency point
}
//To obtain the subscript of the second adjacent node of a node, the subscript of the current node and the subscript of the previous adjacent node are required.
public int getNextNeighbor(int index,int firstNeighbor){
//index the subscript of the current node. First indicates the subscript of the first adjacent node, which itself has been used.
//Get the current node and the subscript of the second adjacency point
//After all, a node may have many adjacent nodes
for(int j = firstNeighbor + 1;j < vertexList.size();j++){
if(edges[index][j] == 1){
return j;//Return the subscript of the second adjacent contact
}
}
return -1;//No second neighbor node returns - 1
}
//Return node according to subscript
public String getValueOfIndex(int index){
return vertexList.get(index);
}
public int getedgesNums(){
//Returns the number of nodes
return vertexList.size();//Returns the number of nodes
}
//Return weight according to subscript
public int getWeight(int v1,int v2){
return edges[v1][v2];
}
public void show(){
//The display matrix is very simple. Just traverse the two-dimensional array directly
for(int[] link : edges){
for(int temp : link){
System.out.print(temp + " ");
}
System.out.println();
}
}
public int getNumOfedes(){//Returns the number of edges
//An edge represents a connection
return numOfedes;
}
public void insert(String vertex){
vertexList.add(vertex);
}
public void insertedges(int v1,int v2,int weight){
//Record matrix
//Subscripts with values in the matrix are represented by 1
//v1 represents the subscript of the first vertex and v2 represents the subscript of the second vertex.
edges[v1][v2] = weight;
edges[v2][v1] = weight;
numOfedes++;
}
}
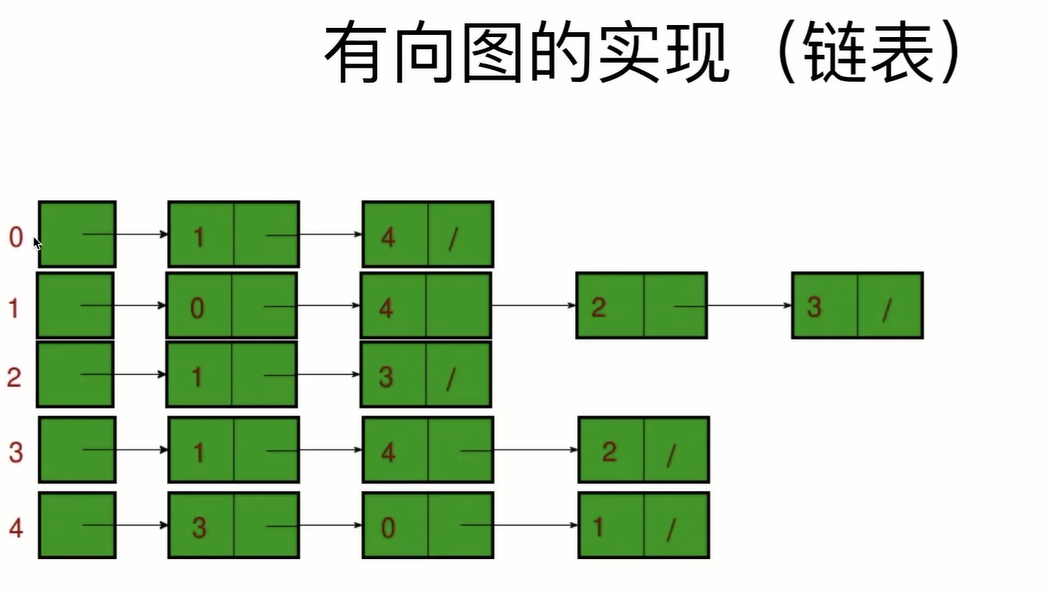
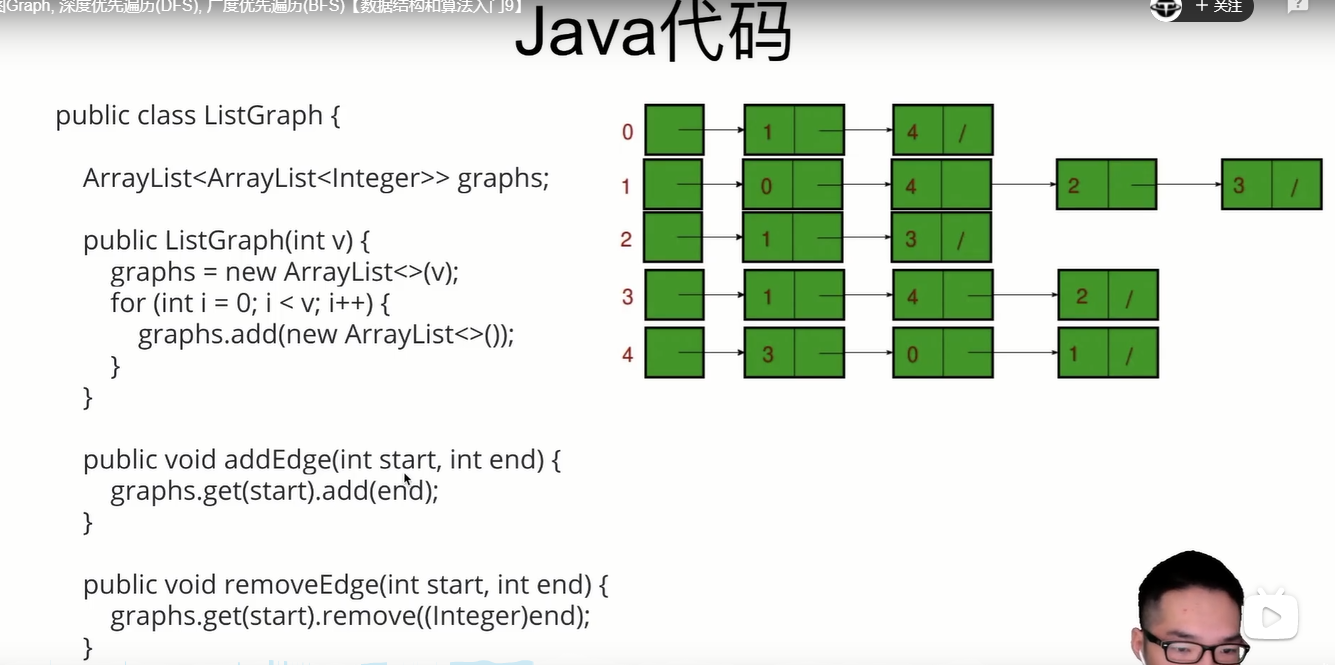
Directed graphs are better stored in this way.
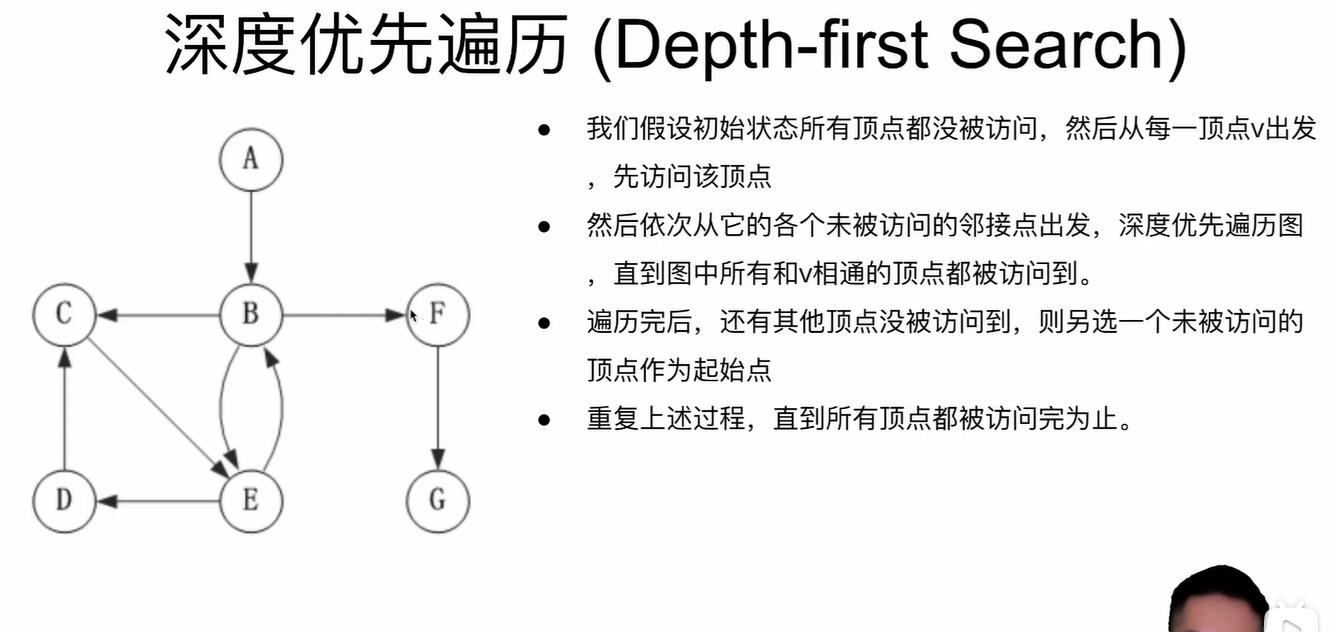
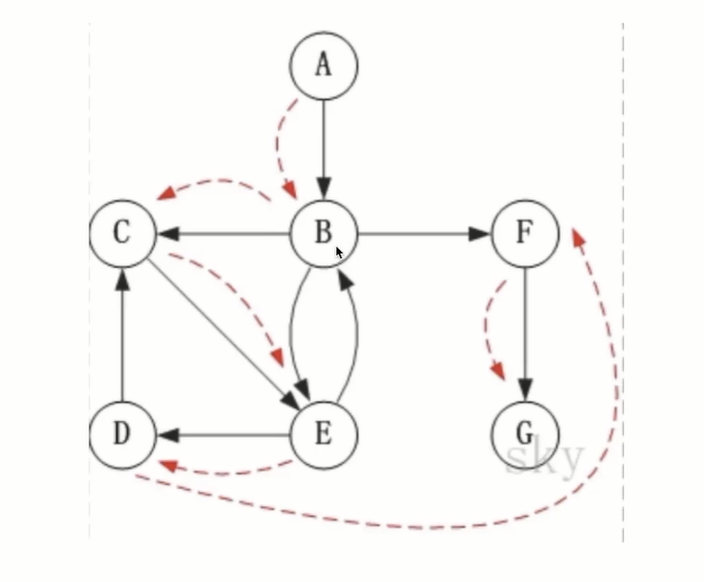
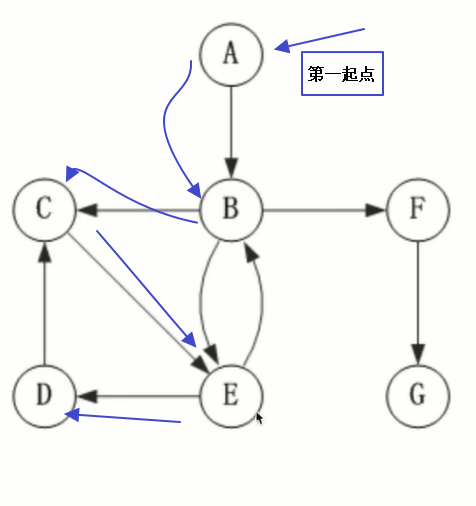
The nodes are accessed one by one according to the storage order. As long as the nodes are connected according to the storage order, they will be accessed one by one.
When there is no connection, find another node as the second starting point
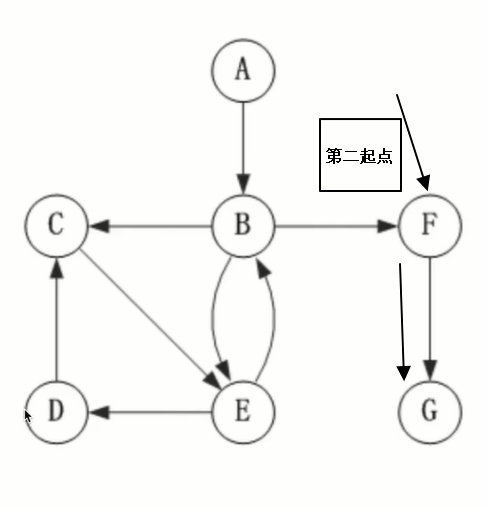
What is a neighbor node? Is to follow the linked list in order, and find a new starting point when you can't go.

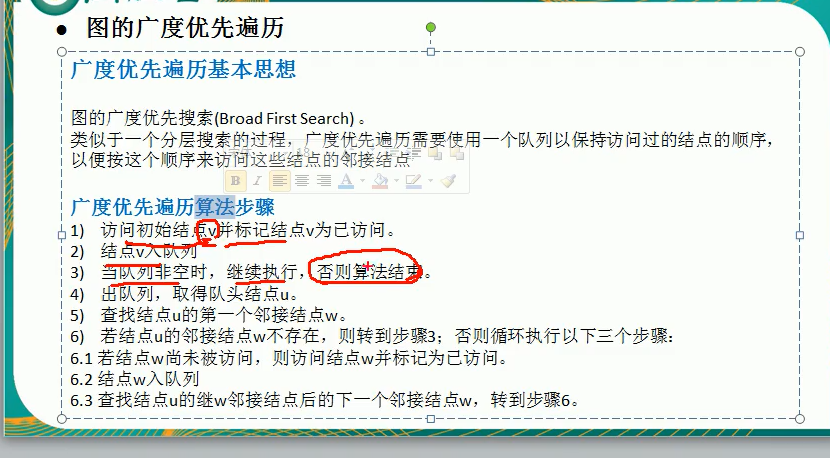
breadth-first search
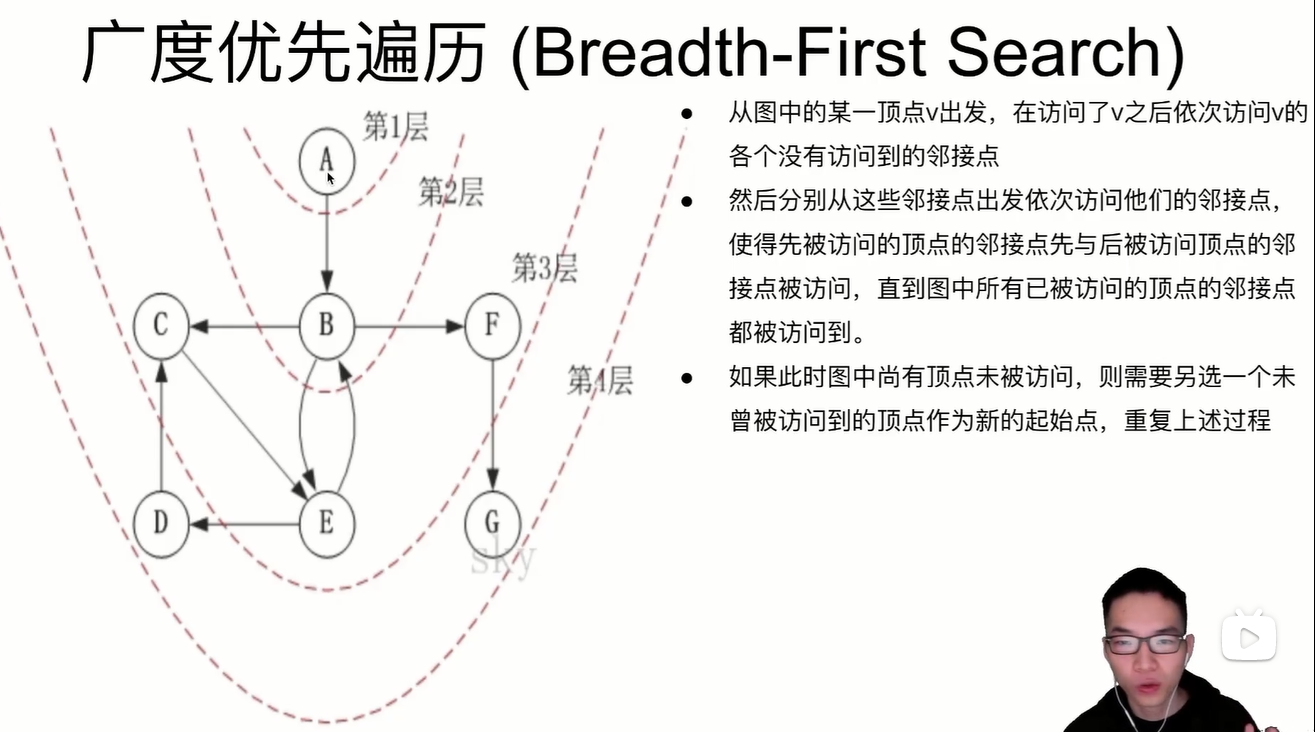
First access all the nodes of a node, and then access all the adjacent nodes of their own adjacent nodes.
To put it bluntly
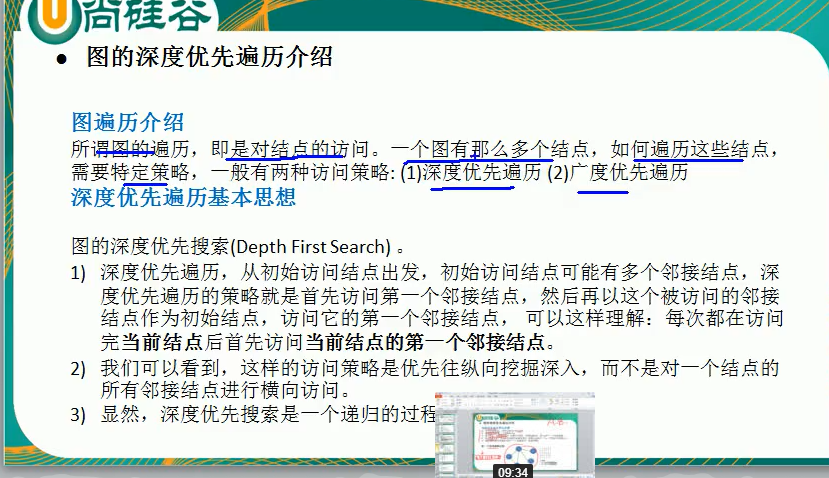
Depth first, just like a bear breaking a stick, if you don't study hard, you will study deeply. Learn deeply first, and then make up a little bit. Just like reading history books, first read all the 5000 years up and down to know what the change of dynasties looks like, and then make up history from Dynasty to Dynasty.
Breadth first means, to put it bluntly, start with the Qin Dynasty, read dozens of books, understand the Qin Dynasty very well, then look at the Han Dynasty, read dozens of books, and then look down.
Depth first means that when attacking, regardless of the enemy in the rear, they boldly insert and risk their lives to insert,
After interleaving, turn back and clear the enemy in the rear.
Breadth first is to clear all obstacles before, after, and then push forward.