These questions are simple and difficult, so you may think of many solutions as soon as you see the questions.
In this paper, the idea of double pointer is used to solve the problem. [left and right pointer, fast and slow pointer]

977. Square of ordered array

Go and do the problem

• Give you an integer array nums sorted in non decreasing order, and return a new array composed of the square of each number. It is also required to sort in non decreasing order.

1. A new array is used to store the squared array
2. Let i = 0, j = n-1 -- > [nums [i] * nums [i] > nums [J] * nums [J]] be compared and stored in a new array.

public int[] sortedSquares(int[] nums) {
	int n = nums.length;
	int[] ans = new int[n];
	int i = 0, j = n-1;
	for(int p=n-1; i<=j; p--){
		if(nums[i]*nums[i] > nums[j]*nums[j]){
			ans[p] = nums[i]*nums[i];
			i++;
		}else{
			ans[p] = nums[j]*nums[j];
			j--;
		}
	}
	return ans;
}

283. Move zero

Go and do the problem

• Given an array num, write a function to move all zeros to the end of the array while maintaining the relative order of non-zero elements.

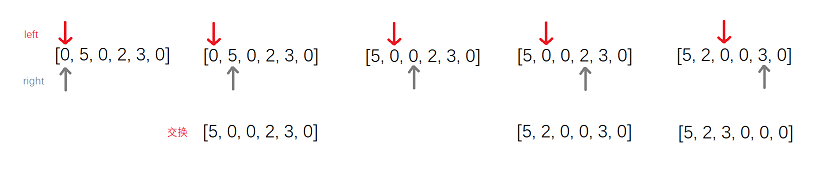
1. The left pointer points to the tail of the currently processed sequence, and the right pointer points to the head of the sequence to be processed
2. Initially, it points to nums[0], and the right pointer traverses forward. If it is not zero, it will be exchanged with the left pointer
3. Perform an exchange and move the left pointer one bit to the right
   Example: [0, 5, 0, 2, 3, 0]

	public void moveZeroes(int[] nums) {
        int n = nums.length, left = 0, right = 0;
        while(right < n){
            //Each cycle, the right pointer moves one bit to the right
            if(nums[right] != 0){
            	//Perform the exchange and move the left pointer one bit to the right
                swap(nums, left, right);
                left++;
            }
            right++;
        }
    }
    //exchange
    public void swap(int[] nums, int left, int right){
        int temp = nums[left];
        nums[left] = nums[right];
        nums[right] = temp;
    }

167. Sum of two II - input ordered array

Go and do the problem

• Given an integer array numbers that has been arranged in non decreasing order, please find out that the sum of the two numbers in the array is equal to the target number target.
  The function should return the subscript values of these two numbers as an array of integers of length 2. The subscript of numbers starts counting from 1, so the answer array should meet 1 < = answer [0] < answer [1] < = numbers.length.
  You can assume that each input only corresponds to a unique answer, and you can't reuse the same elements.

1. The two pointers point to numbers[0] and numbers[n-1], respectively
2. Calculate the sum of two elements pointed to by two pointers at a time and compare it with the target value.

    public int[] twoSum(int[] numbers, int target) {
        int left = 0, right = numbers.length-1;

        while(left < right){
            int sum = numbers[left] + numbers[right];
            if(sum == target){
                return new int[]{left + 1, right + 1};
            }else if(sum < target)
                left++;
            else
                right--;
        }

        return new int[]{-1, -1};
    }

344. Reverse string

Go and do the problem

• Write a function that inverts the input string. The input string is given as a character array s.
  Do not allocate additional space to another array. You must modify the input array in place and use the additional space of O(1) to solve this problem.

1. The two pointers point to s[0] and s[n-1] respectively
2. Swap the elements pointed to by the two pointers

	public void reverseString(char[] s) {
        int n = s.length;
        int left = 0;
        int right = n-1;
        while(left < right){
            char temp = s[left];
            s[left++] = s[right];
            s[right--] = temp;
        }
    }

876. Intermediate node of linked list

Go and do the problem

• Given a non empty single linked list with head node, return the intermediate node of the linked list.
  If there are two intermediate nodes, the second intermediate node is returned.

1. The fast pointer takes two steps and the slow pointer takes one step.
2. The fast pointer traversal ends, and the slow pointer should point to the intermediate node

public ListNode middleNode(ListNode head) {
    ListNode slow = head, fast = head;
    while(fast != null && fast.next != null){
        fast = fast.next.next;
        slow = slow.next;
    }
    return slow;
}

19. Delete the penultimate node of the linked list

Go and do the problem

• Give you a linked list, delete the penultimate node of the linked list, and return the head node of the linked list.
  Advanced: can you try using one scan?

1. The fast pointer takes n steps more than the slow pointer. When the fast pointer is finished, the slow pointer points to the penultimate node to be deleted.
2. Implementation: first make the fast pointer traverse forward n times, and then the two pointers traverse forward together until the fast pointer is empty.
3. In order to make the slow pointer point to the precursor node of the node to be deleted at the end of traversal, consider initially pointing the slow pointer to the dummy node.

public ListNode removeNthFromEnd(ListNode head, int n) {
    ListNode dummy = new ListNode(0, head);
    ListNode slow = dummy, fast = head;
    for(int i = 0; i < n; i++){
        fast = fast.next;
    }
    while(fast != null){
        slow = slow.next;
        fast = fast.next;
    }
    slow.next = slow.next.next;
    ListNode ans = dummy.next;
    return ans;
}

🐑🐑🐑