Select sort

Sorting principle:

1. During each traversal, it is assumed that the element at the first index is the minimum value, which is compared with the values at other indexes in turn. If the value at the current index is greater than the value at some other index, it is assumed that the value derived from some other index is the minimum value, and finally the index where the minimum value is located can be found
2. Swap the values at the first index and at the index where the minimum value is located
   
   

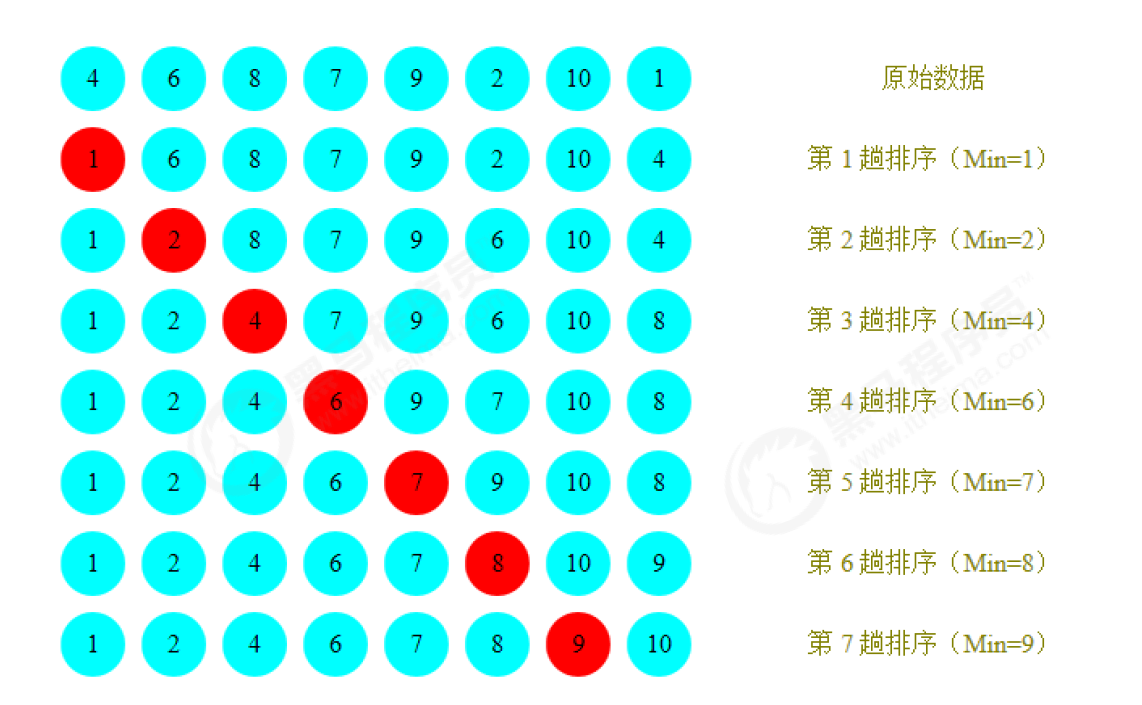
Code implementation:

public class SelectSort {
    public static void selectSort(int[] data) {
        System.out.println("Start sorting");

        int arrayLength = data.length;
        for (int i = 0; i < arrayLength - 1; i++) {
            int minIndex = i;
            for (int j = i + 1; j < arrayLength; j++) {
                if (data[minIndex] - data[j] > 0) {
                    minIndex = j;
                }
            }
            if(minIndex != i){
                int temp = data[i];
                data[i] = data[minIndex];
                data[minIndex] = temp;
            }
            System.out.println(java.util.Arrays.toString(data));
        }
    }

    public static void main(String[] args) {
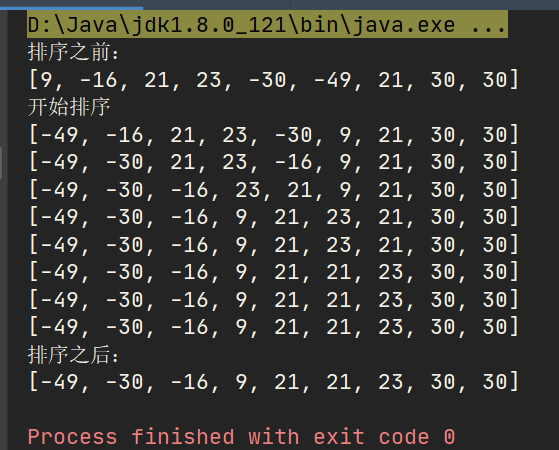
        int[] data = { 9, -16, 21, 23, -30, -49, 21, 30, 30 };
        System.out.println("Before sorting:\n" + java.util.Arrays.toString(data));
        selectSort(data);
        System.out.println("After sorting:\n" + java.util.Arrays.toString(data));
    }
}

Instability of selection sorting

DataWrap

public class DataWrap implements Comparable<DataWrap>{
    int data;
    String flag;
    public DataWrap(int data,String flag){
        this.data = data;
        this.flag = flag;
    }
    public String toString(){
        return data + flag;
    }
    //The size of the two datawraps is determined according to the data instance variable
    @Override
    public int compareTo(DataWrap dw) {
        return this.data > dw.data? 1 : (this.data == dw.data? 0 : -1);
    }
}

SelectSort2

public class SelectSort2 {
    public static void selectSort(DataWrap[] data) {
        System.out.println("Start sorting");
        int arrayLength = data.length;
        for (int i = 0; i < arrayLength - 1; i++) {
            int minIndex = i;
            for (int j = i + 1; j < arrayLength; j++) {
                if (data[minIndex].compareTo(data[j]) > 0) {
                    minIndex = j;

                }
            }
            if(minIndex != i){
                DataWrap temp = data[i];
                data[i] = data[minIndex];
                data[minIndex] = temp;
            }
            System.out.println(java.util.Arrays.toString(data));
        }
    }

    public static void main(String[] args) {
        DataWrap[] data = { new DataWrap(5, "*"), new DataWrap(8, ""),
                new DataWrap(5, ""), new DataWrap(-49, ""),
                new DataWrap(30, "*"), new DataWrap(22, ""),
                new DataWrap(30, "") };
        System.out.println("Before sorting:\n" + java.util.Arrays.toString(data));
        selectSort(data);
        System.out.println("After sorting:\n" + java.util.Arrays.toString(data));
    }
}

5 * it was sorted before 5. In the new array, it was ranked after 5

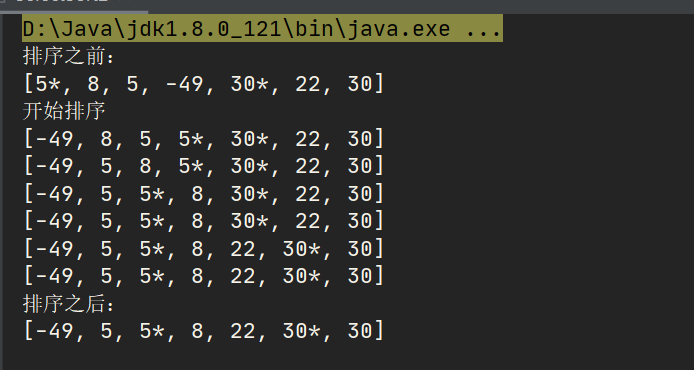
We know that if the first element 5 is selected for the first time, it will exchange with - 49, and the relative front and rear order of the two 5 in the original sequence will be destroyed. Therefore, selective sorting is not a stable sorting algorithm.

Time complexity analysis:

The selection sorting uses a double-layer for loop, in which the outer loop completes data exchange and the inner loop completes data comparison, so we make statistics respectively

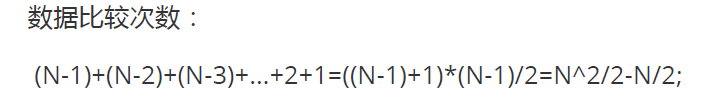
Average: T(n) = O(n2)

• Best case: T(n) = O(n2)
• Worst case: T(n) = O(n2)
• Average: T(n) = O(n2)

Comparison: bubble sort and selection sort

1. Bubble sorting is to compare two numbers in adjacent positions, while selective sorting is to compare in order to find the maximum or minimum value;
2. After each round of comparison of bubble sorting, if the position is wrong, you need to change the position. If sorting is selected, you only need to change the position once for each round of comparison;
3. Bubble sorting is to find the location through the number, and selection sorting is to find the number for the location;

Advantages and disadvantages of bubble sorting:

• advantage:
  Relatively simple, low spatial complexity and stable;

• Disadvantages:
  Time complexity is too high and efficiency is slow;

Advantages and disadvantages of selecting sorting:

• advantage:
  A round of comparison only needs to change the position once;

• Disadvantages:
  Slow and unstable efficiency