Summary

• Bubble, Select, Insert, Merge, Fast, Hill, Heap Sort, are all sort based on comparison
  • The lowest average complexity is O(nlog(n))
• Count, bucket, cardinality sort, not comparison-based sort
  • Is a typical space-exchange time, and in some cases, the average time complexity can be lower than O(nlog(n))

Core Ideas

• Count the number of occurrences of each integer in the sequence and derive the index of each integer in the ordered sequence

Execute process

• First you need to find the maximum max in the array or set arr that needs to be sorted
• Create an array counts of length max + 1[]
• Traversing through an array counts[arr[i]++ for each value in the array that counts the number of different values in the array;
• Then iterate through the counts array, putting the value at the index that is not 0 in turn in the arr array

Example

Code (Version 1)

public class CountingSort {

    public static void sort(int[] arr) {
        //Find the Maximum
        int max = arr[0];
        //Array length
        int n = arr.length;
        for (int i = 1; i < n; ++i) {
            if (arr[i] > max) {
                max = arr[i];
            }
        }

        //Open up memory space to store the number of occurrences of each integer
        int[] counts = new int[1 + max];
        //Count the number of occurrences of each integer
        for (int i = 0; i < n; ++i) {
            ++counts[arr[i]];
        }

        //Sort integers according to the number of times they occur
        int index = 0;
        for (int i = 0; i < counts.length; ++i) {
            while (counts[i]-- > 0) {
                arr[index++] = i;
            }
        }
    }

    public static void main(String[] args) {
        int[] arr = new int[]{7,1,2,3,4,5,6,6,7};
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

test

Problem

• Negative integers cannot be sorted
• And its waste of memory space
• Is an unstable sort

Code (Version 2) (Resolve the above problem)

public static void sort(int[] arr) {
        int n = arr.length;
        if (n <= 1) {
            return;
        }

        //Find the Value
        int max = arr[0];
        int min = arr[0];
        for (int i = 1; i < n; ++i) {
            max = Math.max(max, arr[i]);
            min = Math.min(min, arr[i]);
        }

        //Open up memory space, storage times
        int[] counts = new int[max - min + 1];
        //Count the number of occurrences of each integer. The index of the elements in the ARR array corresponding to the counts array is arr[i] - min.
        for (int i = 0; i < n; ++i) {
            ++counts[arr[i] - min];
        }

        //counts array is no longer saved number of times, change it to prefix and
        for (int i = 1; i < counts.length; ++i) {
            counts[i] += counts[i - 1];
        }

        //Staging all elements with a new array
        int[] newArray = new int[n];
        int i = n - 1;
        //Traverse the element backwards and forwards, placing it in an appropriate place in an ordered array to ensure stability
        while (i >= 0) {
            //--counts[arr[i] - min]: Find a new location for arr[i]
            newArray[--counts[arr[i] - min]] = arr[i];
            --i;
        }

        //Assigning an ordered array back to its original array
        while (++i < n) {
            arr[i] = newArray[i];
        }

    }

Complexity

• Time complexity: O(n + k),n is the number of elements, K is the range size of elements [min, max]
• Spatial complexity: O(n + k),n is the number of elements, K is the range size of elements [min, max]

test

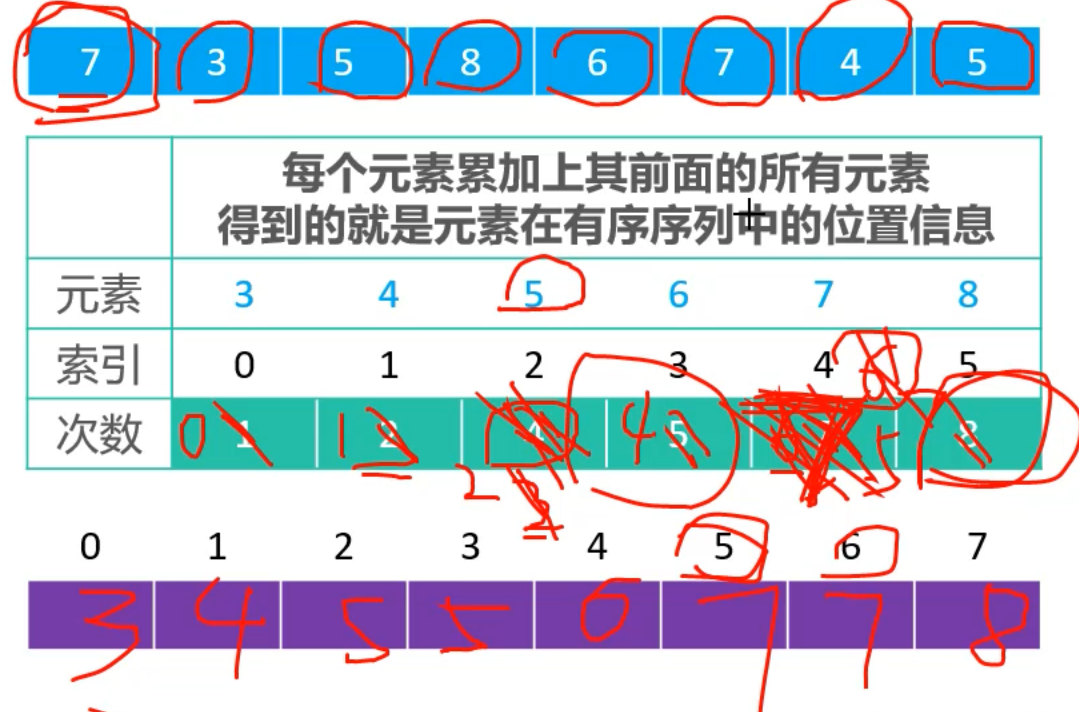
Execution process (illustration)

• Original Array
  
• Find the min and Max in the array, define a new counts array, size max - min + 1, to store the number of occurrences of each element
  
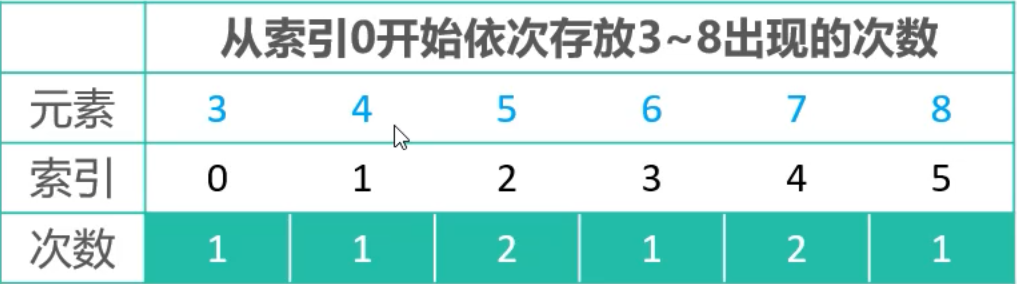
• Find the prefix and sum of the counts array
  
• Then traverse the original array from right to left
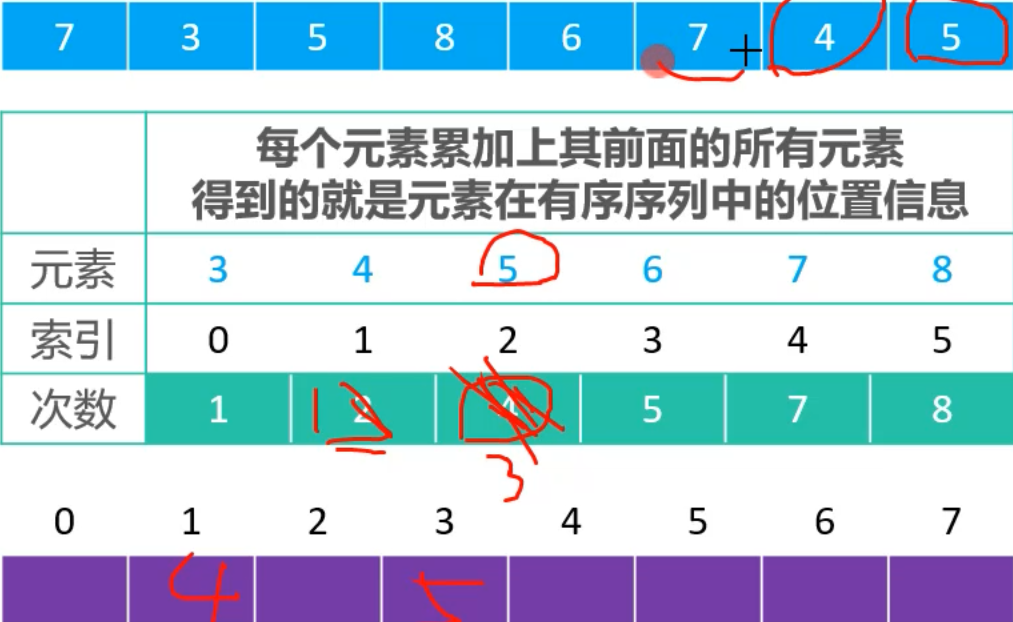
• The first element on the right, 5, corresponds to the prefix of the counts array and 4,4 minus itself. The resulting 5 is subscript 3 in the array and put in, where a new array is used to temporarily store the data
  
• It then traverses to 4,4 corresponding to the prefix and 2, -2 in the counts array, so the index for 4 is 1
  
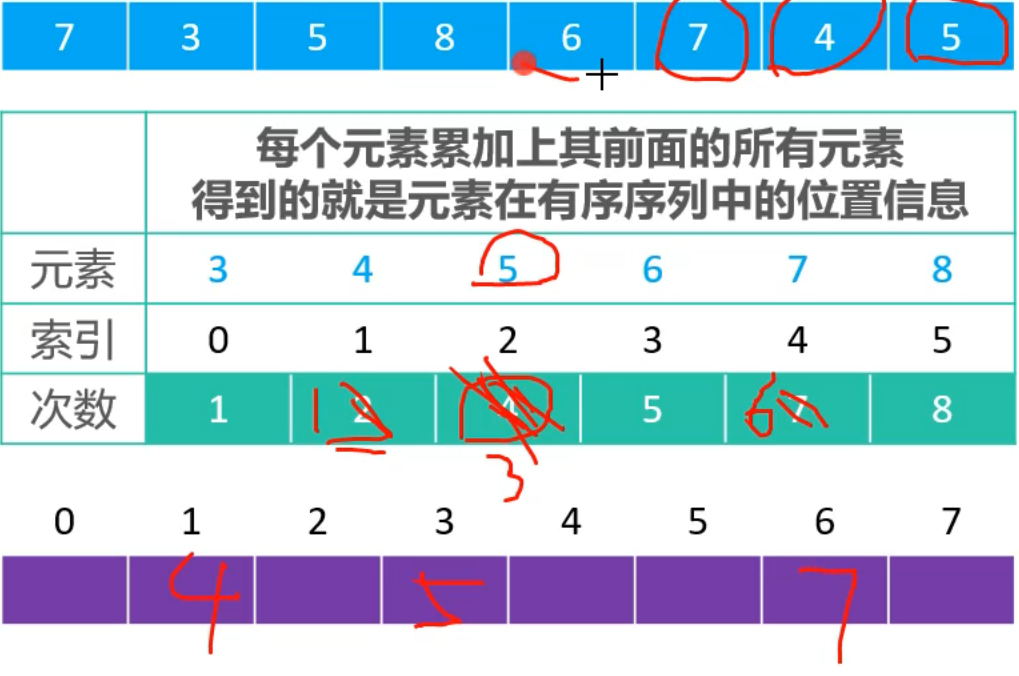
• Then iterate through the 7,7 prefix in the counts array and the corresponding sum is 7,7 - so the new index position is 6
  
• . . .
• Then, as above, the final result is
  

Use scenarios

• Sort numbers with a range