1, Introduction to fast platoon

Quick sort uses the idea of divide and conquer. Its basic idea is:

1. Select a keyword key and place it in the sorted position of the whole sequence through one sorting, and its left sequence is less than or equal to key.
   The right sequence is greater than or equal to key.

2. Recursively continue the first step of sorting the divided two subsequences.

Illustration:

2, Partial sorting

1. Hoare method

Left is selected as keyi by default. Find an element smaller than the key on the right and an element larger than the key on the left. Exchange the two elements. When left == right equals. At this point, their location is where the key is finally sorted. Exchange key and left.

Note:

Select left for the keyword. Right has to find it first. Only in this way can we ensure the correctness. If the keyword is right, otherwise.

Code example:

int PartSort1(int* arr, int left, int right)
{
	int keyi = left;

	while (left < right)
	{
		while (left < right && arr[right] >= arr[keyi])
			right--;
		while (left < right && arr[left] <= arr[keyi])
			left++;
		Swap(&arr[left], &arr[right]);
	}
	Swap(&arr[keyi], &arr[left]);
	return left;
}

2.hole method

In the deformation of hoare method, the keyword key is left. Assuming that left is a pit, find a filling pit smaller than key from the right. At this time, the position of the filled number forms a new pit, and then find a number larger than key from the right to fill the new pit. Cycle back and forth. When left == rihgt, the position of the pit is the position after key sorting. Fill in the key.

Code example:

int PartSort2(int* arr, int left, int right)
{
	int hole = left;
	int key = arr[hole];

	while (left < right)
	{
		while (left < right && arr[right] >= key)
			right--;

		arr[hole] = arr[right];
		hole = right;

		while (left < right && arr[left] <= key)
			left++;

		arr[hole] = arr[left];
		hole = left;
	}

	arr[hole] = key;
	return hole;
}

3. Double finger acupuncture

1. prev points to an element with a subscript of 0 and cur points to an element with a subscript of 1.
2. Cur moves back. If arr[cur] is less than key, prev + +, and exchange the elements where prev and cur are located.
3. At the end of the iteration, the position of prev is the final position of the key.

Code example:

int PartSort3(int* arr, int left, int right)
{
	int cur = 1, prev = 0;
	int keyi = left;

	while (cur <= right)
	{
		if (arr[cur] <= arr[keyi] && ++prev != cur)
			Swap(&arr[cur], &arr[prev]);
		++cur;
	}

	Swap(&arr[prev], &arr[keyi]);
	return prev;
}

3, Recursive implementation

When left > = right, it indicates that there is only one element at most in the interval to be sorted. By default, it is ordered and there is no need to sort.

Code example:

void QuickSort(int* arr, int left, int right)
{
	if (right <= left)
		return;

	int keyi = PartSort1(arr, left, right);

	QuickSort(arr, left, keyi - 1);
	QuickSort(arr, keyi + 1, right);
}

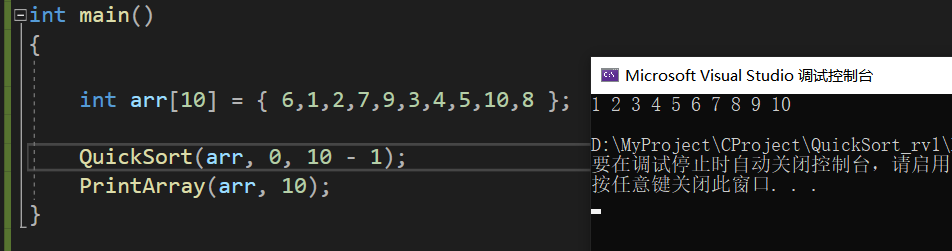
Operation screenshot:

4, Sorting optimization

Previously, our key selection is always the leftmost number of the sequence to be arranged. However, when the sequence to be arranged is orderly or close to orderly, the efficiency will become very low.

Example of problem:

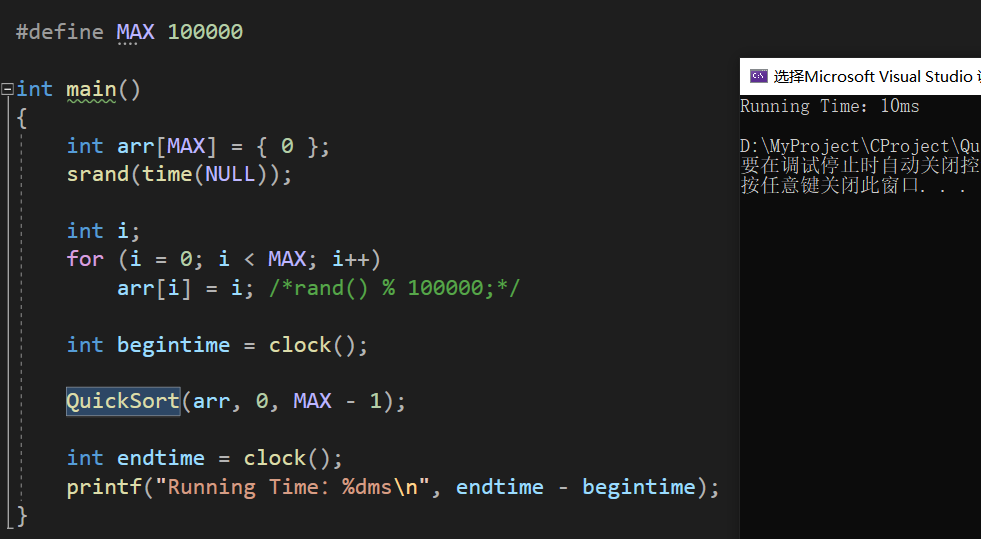
When the array is ordered, the average complexity is O(N^2), and the stack overflows after sorting 10000 numbers.

When the array to be arranged is a random number, the efficiency returns to O(N * logN). The number of 100000 is also sorted quickly.

resolvent:

1. Take a random number.

2. The three digit median method takes the median among the numbers pointed to by the three subscripts of left right mid.

Code example:

int PartSort1(int* arr, int left, int right)
{
	//The three digit median is also valid when the sequence to be arranged is orderly
	int mid = GetMid(arr, left, right);
	Swap(&arr[left], &arr[mid]);
	int keyi = left;

	while (left < right)
	{
		while (left < right && arr[right] >= arr[keyi])
			right--;
		while (left < right && arr[left] <= arr[keyi])
			left++;
		Swap(&arr[left], &arr[right]);
	}
	Swap(&arr[keyi], &arr[left]);
	return left;
}

At this time, 100000 ordered sequences can also ensure efficiency.

.